Расчет активности цепочки за время компании. Определение изменения активности для 10ти временных точек в абсолютных единицах (БК) для цепочки с данным а
 Скачать 323.35 Kb. Скачать 323.35 Kb.
|
ОПРЕДЕЛЕНИЕ ИЗМЕНЕНИЯ АКТИВНОСТИ ДЛЯ 10-ТИ ВРЕМЕННЫХ ТОЧЕК В АБСОЛЮТНЫХ ЕДИНИЦАХ (БК) ДЛЯ ЦЕПОЧКИ С ДАННЫМ А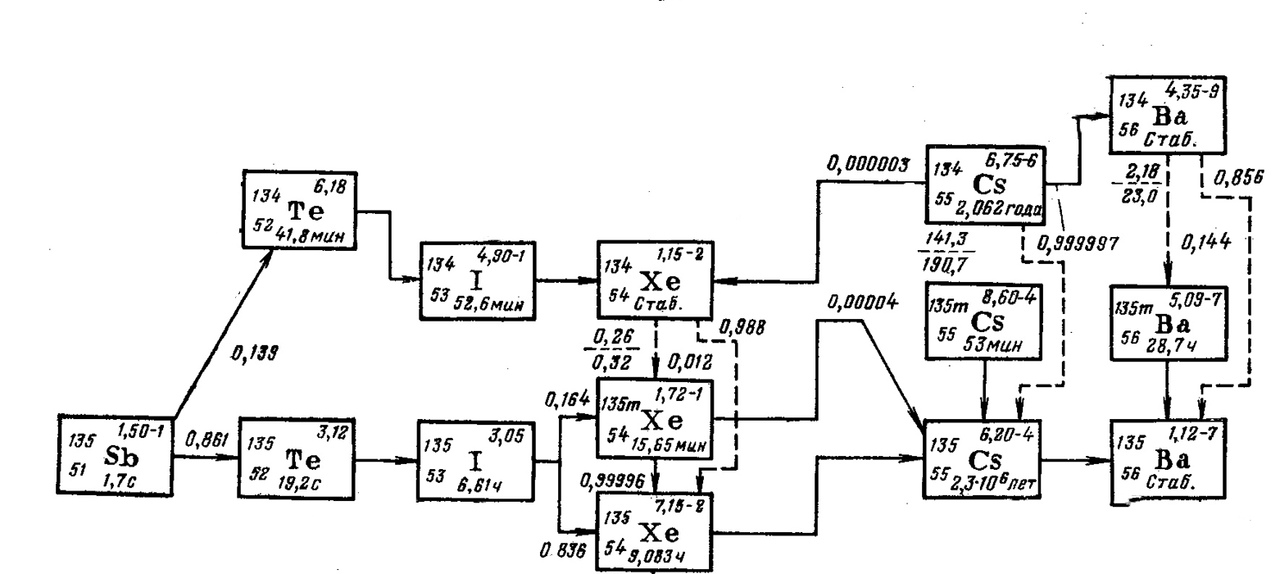 Рисунок 1 – Цепочка с А = 135 Рисунок 1 – Цепочка с А = 135Как видно, здесь есть и уход в более легкую цепочку с А = 134 и два ветвления – у Sb и I (здесь и далее порядковые номера и массовые числа будут опущены, т.к. цепочка уже выбрана). Мы можем рассчитывать только линейные цепочки (с одним или несколькими входами). В данном случае таких цепочек будет две: Sb Te I Xe Cs Ba Sb Te I mXe Xe Cs Ba Таблица 10 Характеристики радионуклидов цепочки с А = 135
Расчеты характеристик нуклидов цепочки с А =135: 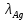 = = 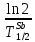 = = 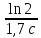 = 0,4077 = 0,4077 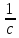 . .Выход каждого изобара (нуклида цепочки с А= 135) можно охарактеризовать независимым выходом ɳнез, который дается в процентах от общего числа делений – абсолютный независимый выход (ɳн.а). В цепочке следующие друг за другом ядра накапливаются за счет распада предшественников. Таким образом, все ядра цепочки, кроме первого, можно считать образующимися по двум каналам: за счет деления и за счет распада предшественников, тогда общее поступление будет описываться кумулятивным выходом 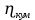 = = 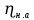 + + 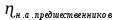 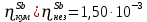 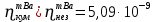 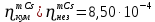 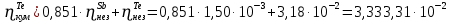 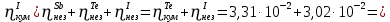 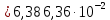 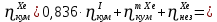 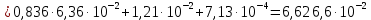 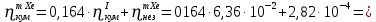 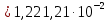 Кажется у 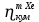 и и 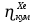 все ОК? все ОК?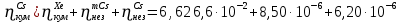 = =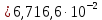 F = 3·1016·W = 3·1016 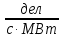 ·1415 МВт = 4,245·1019 ·1415 МВт = 4,245·1019 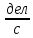 ; ;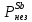 = F · = F · 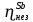 = 4,245·1019 = 4,245·1019 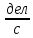 · · 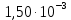 = = 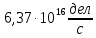 ; ;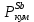 = = 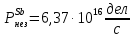 ; ;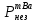 = F · = F · 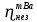 = 4,245·1019 = 4,245·1019 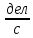 · · 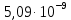 = = 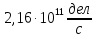 ; ;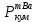 = = 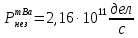 ; ;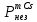 = F · = F · 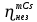 = 4,245·1019 = 4,245·1019 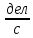 · · 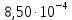 = = 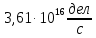 ; ;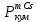 = = 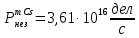 ; ;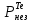 = F · = F · 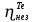 = 4,245·1019 = 4,245·1019 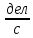 · · 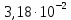 = = 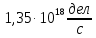 ; ;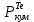 = F · = F · 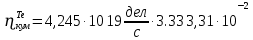 = = 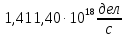 ; ;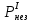 = F · = F · 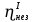 = 4,245·1019 = 4,245·1019 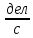 · · 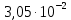 = = 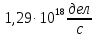 ; ;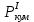 = F · = F · 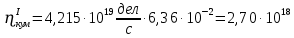 ; ;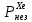 = F · = F · 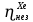 = 4,245·1019 = 4,245·1019 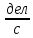 · ·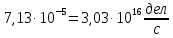 ; ;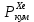 = F · = F · 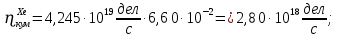 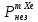 = F · = F · 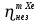 = 4,245·1019 = 4,245·1019 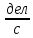 · · 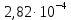 = =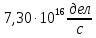 ; ;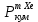 = F · = F · 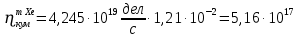 ; ;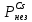 = F · = F · 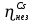 = 4,245·1019 = 4,245·1019 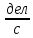 · · 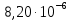 = =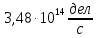 ; ;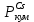 = F · = F · 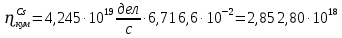 . .ИЗМЕНЕНИЕ АКТИВНОСТИ ЗА ВРЕМЯ КАМПАНИИ Цепочка 1 Для расчета эволюции нуклидов цепочки будут использоваться 10 временных точек: 0T1/2, 0,5T1/2, 1T1/2, 2T1/2, 3T1/2, 4T1/2, 5T1/2, 6T1/2, 8T1/2, 10T1/2, 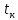 . .Накопление Sb Материнским нуклидом, «родоначальником» цепочки 1, является 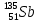 , имеющий очень малый период полураспада и, в соответствии с правилом десяти периодов полураспада, активность данного нуклида вырастет до своего максимума и выйдет практически на постоянное значение в течение 17 с, т. е. скорость поставки , имеющий очень малый период полураспада и, в соответствии с правилом десяти периодов полураспада, активность данного нуклида вырастет до своего максимума и выйдет практически на постоянное значение в течение 17 с, т. е. скорость поставки 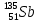 можно принять постоянной, состоящей из собственного независимого выхода. можно принять постоянной, состоящей из собственного независимого выхода.Количество ядер 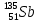 на момент времени кампании на момент времени кампании 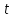 рассчитывается по формуле Бейтмана: рассчитывается по формуле Бейтмана: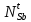 = = 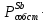 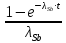 Таблица 11 – Изменение активности 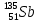 , за время кампании , за время кампании
Накопление Te Считаем, что скорость поставки 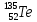 постоянна и состоит из собственного независимого выхода и 85,1% от постоянной активности предшественника - постоянна и состоит из собственного независимого выхода и 85,1% от постоянной активности предшественника - 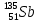 (85,1% (85,1% 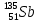 распадается на распадается на 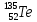 , 13,9% - на , 13,9% - на 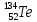 . Тогда: . Тогда: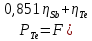 ) )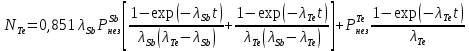 Здесь первое слагаемое учитывает эволюцию Te за счет накопления и распада Sb, а второе - за счет собственного независимого выхода. Таблица 12 – Изменение активности 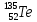 , за время кампании , за время кампании
Накопление I Считаем, что скорость поставки 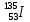 постоянна во времени и включает независимые выходы постоянна во времени и включает независимые выходы 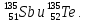 Для упрощения формулы Бейтмана можно использовать правило для случая пары следующих друг за другом изобар: если значение 10T1/2 предшествующего изобара больше значения 0,5T1/2 следующего изобара, то в формуле Бейтмана будут фигурировать оба члена, отвечающие обоим изобарам, а если наоборот – один член, следующий вторым, т.к. вклад распада от предшествующего изобара в эволюцию следующего за его 0,5T1/2 незначителен, поэтому расчет накопления 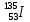 начинается тогда, когда активность его предшественника уже стала постоянной, т.е. его эволюция во времени уже закончилась. Так, начинается тогда, когда активность его предшественника уже стала постоянной, т.е. его эволюция во времени уже закончилась. Так, 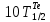 = 197 с = 197 с 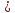 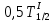 = 11898 с, = 11898 с, 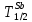 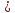 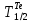 = 11898 поэтому один член (без учета = 11898 поэтому один член (без учета 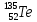 и и 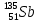 ): ):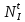 = = 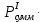 |

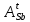 , Бк
, Бк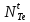
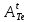 , Бк
, Бк