определение модуля упругости и коэффициента пуассона для стали. Определение модуля упругости и коэффициента Пуассона для стали

• Название: Определение модуля упругости и коэффициента Пуассона для стали
• Анкор: определение модуля упругости и коэффициента пуассона для стали
• Дата: 11.10.2022
• Размер: 136.19 Kb.
• Имя файла: laba_2_sopromat_1.docx
• Тип: Отчет; #727790

ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ



МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение высшего

образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ»

Кафедра механики
Отчет по лабораторной работе № 2
По дисциплине : Сопротивление материалов
Тема: «Определение модуля упругости и коэффициента Пуассона для стали»

Выполнил: студент гр. МЦ-20 ___________ / /

( Подпись)

Проверил: ассистент ___________ /Семёнов В.И./

(Подпись)

Дата:

Санкт-Петербург

2021 год

Цель работы: изучение способа измерения модуля упругости и коэффициента Пуассона, определение упругих констант стали.

Теоретические сведения:

При растяжении стержня в нем возникают продольные напряженияσ_Z и продольныеε_Z и поперечныеε_X деформации. При растягивающих усилиях, соответствующих напряжениям, не превышающим предел текучести, продольные напряжения и деформации связаны соотношением, называемым законом Гука:

σ=E·ε,

где Е – модуль упругости, который также называют модулем Юнга.

Кроме продольных деформаций, в стержне возникают в плоскости, перпендикулярной его оси (поперечные деформации), величину

μ=−ε_X·ε_Z

называют коэффициентом Пуассона.

При нагружении стержня в пределах упругой области коэффициент Пуассона является постоянной величиной и связь между продольными и поперечными деформациями в стержне линейна.

Экспериментальная часть.

Таблица 1. Геометрические параметры образца

t,мм	b,мм	l,мм	F,мм2
6,6	40	40,5	264

Таблица 2. Протокол испытаний

Измеренные величины						Рассчитанные величины
P, кН	∆Z, мм	-∆X, мм	εZ ̲TP ˟10-5	-εX ̲TP˟10-5	σ, МПа		εZ˟10-5	-εX˟10-5
3,2	0,003	0,001	8,1	2,3	12,1		7,41	2,5
6,04	0,006	0,003	17,9	5,2	22,9		14,81	7,5
9,2	0,01	0,004	29,9	8,7	34,9		24,69	10
12	0,013	0,005	40,5	11,8	45,5		32,1	12,5
15	0,017	0,007	52,8	15,3	56,8		41,98	17,5
18,8	0,022	0,009	68,2	19,7	71,2		54,32	22,5
21	0,026	0,009	78	22,5	79,6		64,2	22,5
24	0,031	0,011	90,5	26,1	90,9		76,54	27,5
27	0,035	0,012	102,9	29,7	102,3		86,42	30

Расчётные формулы: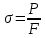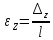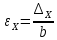







Примеры расчетов:

F=b*t=6,6*40=264 мм²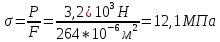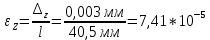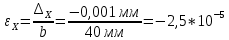







Графическая часть.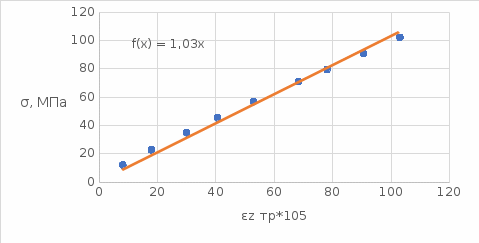



График 1. Зависимость напряжения от деформации, определённой по тензорезисторам.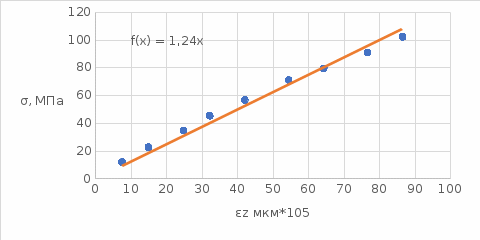



График 2. Зависимость напряжения от деформации, определённой по микрометрам.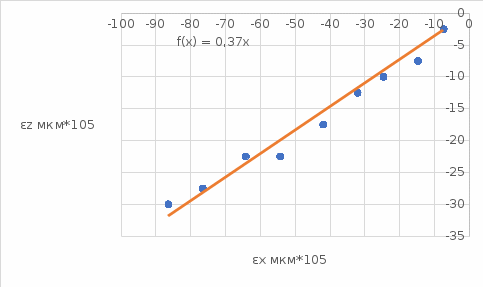



График 3. Зависимость поперечных деформаций от продольных деформаций, оперделённых по микрометрам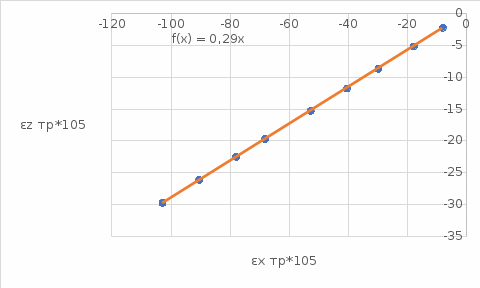



График 4. Зависимость поперечных деформаций от продольных деформаций, оперделённых по микрометрам

Вывод: в ходе лабораторной работы изучили способ измерения модуля упругости и коэффициента Пуассона, определили упругие константы стали.

Для зависимостей σ(ε_Z), рассчитанными по микрометрам и тензорезисторам, модуль упругости составил соответственно E=1,03*10⁵ МПа и E=1,24*10⁵ Мпа.

Для зависимости ε_X(ε_Z), рассчитанной по микрометрам, коэффициент Пуассона составил µ=0,37.

Для зависимости ε_X(ε_Z), рассчитанной по тензорезисторам, коэффициент Пуассона составил µ=0,29.