Определение момента инерции диска с вырезом
 Скачать 180.84 Kb. Скачать 180.84 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Кузбасский государственный технический университет имени Т.Ф. Горбачёва» Кафедра физики Отчёт По лабораторной работе №1 К-303.4 «Определение момента инерции диска с вырезом» Выполнил ст. группы Гришин Александр Сергеевич Преподаватель Кошкина Галина Кронидовна
Приборы и принадлежности: установка для определения момента инерции методом колебаний, штангенциркуль, масштабная линейка, секундомер. Схема экспериментальной установки: 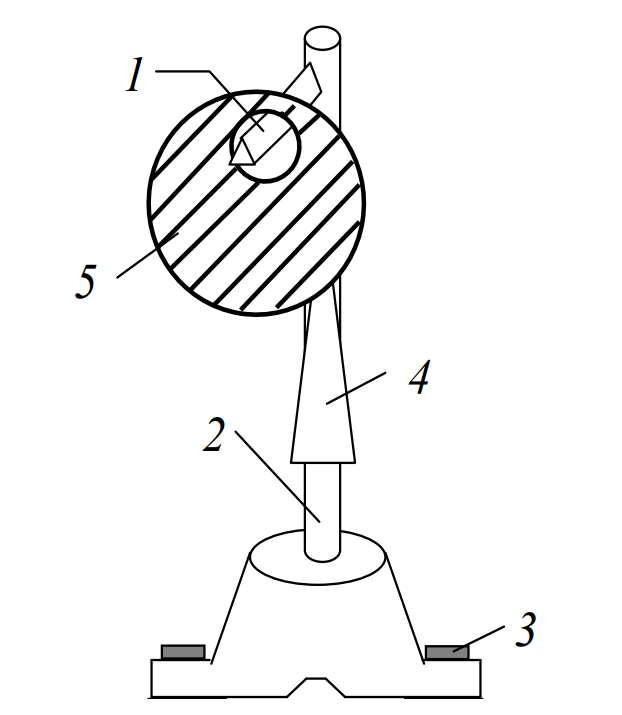 Рис. 1 Схема установки: 1 – призма; 2 – стойка на треноге; 3 – винты; 4 – планка; 5 – диск с вырезом Описание установки: Установка для определения момента инерции методом колебаний состоит из призмы, прикрепленной к вертикальной стойке, помещенной в треногу, две ножки которые снабжены винтами. Это позволяет регулировать установку так, чтобы опорное ребро призмы приняло горизонтально положение. К стойке прикреплена планка клиновидной формы с углом при вершине 4°. Планка служит визиром, позволяющим следить за тем, чтобы размах колебаний не превышал 5°. Методика измерений и расчетов. Момент инерции диска с вырезом может быть определен экспериментально и теоретически. При экспериментальном определении момента инерции тела рассматриваются его свободные гармонические колебания. В данной работе тело – однородный диск радиусом Rс отверстием радиусом r (рис. 2). Если диск с вырезом отклонить от положения равновесия на малый угол 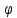 , то он может совершать гармонические колебания под действием силы тяжести относительно неподвижной горизонтальной оси, проходящей через точку D. Точка D пересечения оси колебаний маятника с вертикальной осью Y называется точкой подвеса. Если ось колебаний не проходит через центр масс (точка C), то тело называется физическим маятником. , то он может совершать гармонические колебания под действием силы тяжести относительно неподвижной горизонтальной оси, проходящей через точку D. Точка D пересечения оси колебаний маятника с вертикальной осью Y называется точкой подвеса. Если ось колебаний не проходит через центр масс (точка C), то тело называется физическим маятником.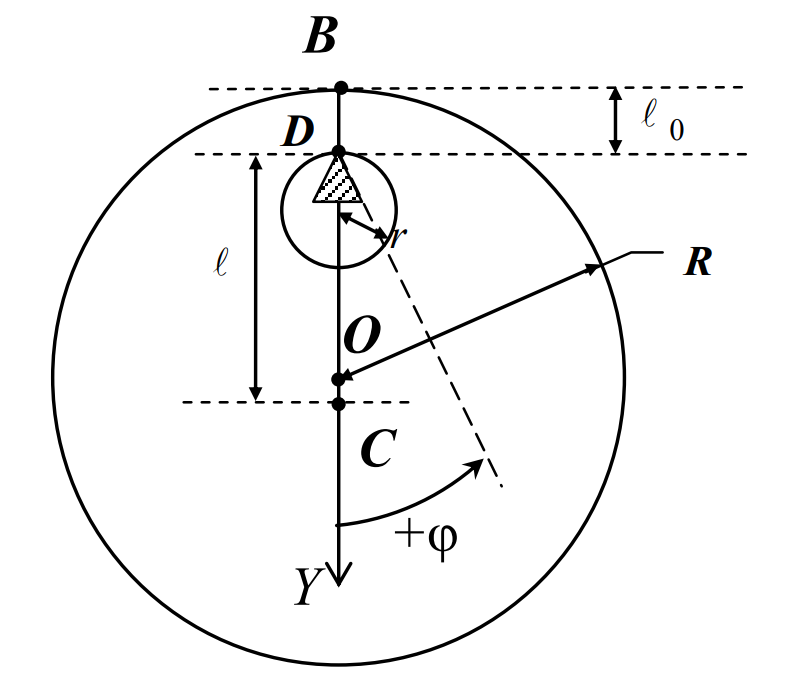 Рис. 2 Диск с вырезом Положение масс диска с вырезом определяется из условия равенства моментов сил относительно оси, проходящей через точку O– центр масс диска без выреза (рис. 3). 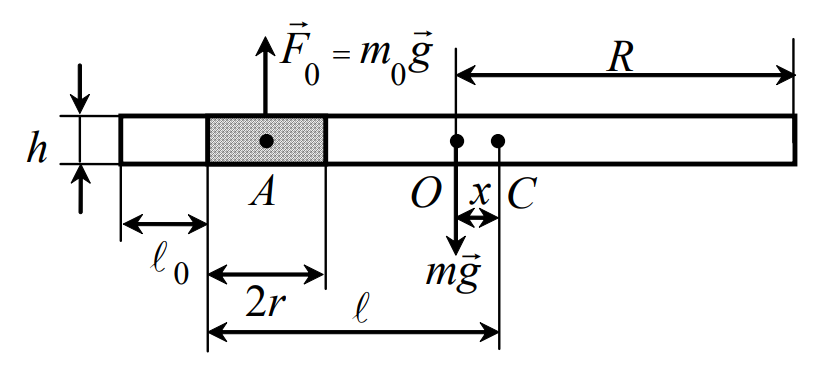 Рис. 3 Схема к расчету положения центра масс диска с вырезом Основные расчетные формулы. Соотношение для расчета расстояния 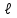 между осью колебаний и осью, проходящей через центр масс физического маятника: между осью колебаний и осью, проходящей через центр масс физического маятника: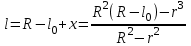 , (1) , (1) где l0 – кратчайшее расстояние от точки подвеса до дуги окружности диска, R – радиус, r – радиус вырезанной части. Масса mсплошного диска и масса m0 вырезанной части: 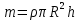 и и 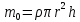 , (2) , (2)где m – масса сплошного диска, m0 – масса вырезанной части диска, h – толщина диска. Считать, что плотность материала диска 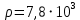 кг/м3. кг/м3.Период колебаний Т маятника: 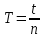 , (3) , (3)где n – число полных колебаний. Экспериментальное значение момента инерции JЭ диска: 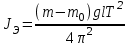 , (4) , (4)где (m – m0) – масса диска с вырезом/ Теоретическое значение момента инерции JTдиска с вырезом: 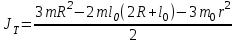 (5) (5)Отклонение εJрезультатов экспериментального и теоретического значений момента инерции физического маятника: 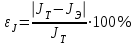 (6) (6)Выполнение расчетов. Таблица 1 Расчет параметров установки
Таблица 2 Расчет момента инерции диска с вырезом n=10
Примеры расчетов. 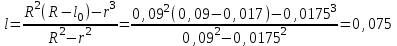 м м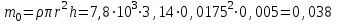 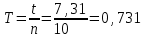 с с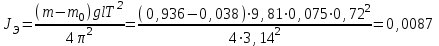 кг∙м2 кг∙м2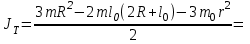 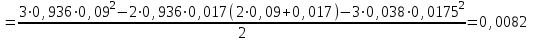 кг∙м2 кг∙м2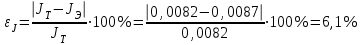 Вывод: в данной лабораторной работе мы определяли момент инерции диска с вырезом относительно оси колебаний, не проходящей через центр масс диска. Момент инерции мы определяли экспериментальным способом, в котором мы использовали колебательную установку. Мы отклоняли диск из положения равновесия и замеряли время, за которое проходит 10 полных колебаний. Для определения момента инерции мы измеряли: радиус диска, радиус вырезанной части диска, кратчайшее расстояние от точки подвеса до дуги окружности диска, толщину диска. С помощью этих параметров мы рассчитали расстояниемежду осью колебаний и осью, проходящей через центр масс физического маятника, массу диска с вырезом, период колебаний, экспериментальной и теоретическое значения момента инерции. Расхождение экспериментального и теоретического значений момента инерции составило 6,1%. |
