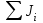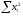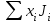Маятник Обербека. Определение момента инерции с помощью маятника Обербека
 Скачать 122.03 Kb. Скачать 122.03 Kb.
|
|
Ф  едеральное государственное бюджетное образовательное учреждение высшего образования Санкт-Петербургский горный университет Кафедра общей и технической физики Отчет по лабораторной работе №6 По дисциплине ФИЗИКА (наименование учебной дисциплины согласно учебному плану) Тема: Определение момента инерции с помощью маятника Обербека Выполнил: студент группы ЭРБ-22-1 ___________ Кладько А. А. (подпись) (Ф.И.О.) Дата: 13.10.2022 Проверил: доцент _____________ Кожокарь М.Ю. (должность) (подпись) (Ф.И.О.) Санкт-Петербург 2022 Цель работы Исследовать зависимость момента инерции крестовины с надетыми на неё грузиками от распределения массы относительно оси вращения, проходящей через центр масс крестовины. Краткие теоретические сведения В основе эксперимента лежит основное уравнение динамики вращательного движения твёрдого тела 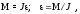 (1) (1)где 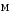 - суммарный момент внешних сил, приложенных к телу относительно оси вращения; J - момент инерции тела относительно той же оси; - суммарный момент внешних сил, приложенных к телу относительно оси вращения; J - момент инерции тела относительно той же оси; 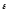 - угловое ускорение. - угловое ускорение.Момент инерции тела является мерой инертности тела при вращательном движении, подобно тому как масса тела является мерой инертности тела при поступательном движении. Момент инерции тела зависит от распределения массы тела относительно оси вращения. Маятник Обербека состоит из крестовины, на стержнях которой находятся грузы. Они могут перемещаться по стержням и закрепляться в нужном положении. Крестовина с грузами насажена на вал, на котором укреплены два шкива различного радиуса. На шкив намотана нить, которая переброшена через блок. К её концу привязана гирька, момент силы тяжести которой уравновешивает момент сил трения. К концу нити подвешивают груз массой m, под действием силы тяжести которого система приводится в движение. На груз действует сила тяжести P=mg и сила натяжения F, поэтому на основании второго закона Ньютона можно записать 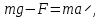 (2) (2)где g - ускорение свободного падения; а - ускорение, с которым движется груз. Крестовина приходит во вращательное движение под действием момента силы натяжения М = Frо , (3) где rо - радиус шкива. Из уравнений (1)-(3) можно получить 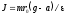 , (4) , (4)Так как угловое ускорение связано с ускорением а соотношением = а/r0 , то формулу (4) можно записать в виде 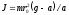 , (5) , (5)где а = 2h/t2; h - путь, пройденный грузом за время t. Таким образом, 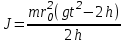 (6) (6)Из теоретических соображений следует, что момент инерции крестовины с четырьмя грузами массой 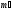 , если считать грузы материальными точками, можно выразить формулой , если считать грузы материальными точками, можно выразить формулой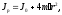 (7) (7)где J0 - момент инерции тела при r = 0. Из формулы (7) следует, что J = f(r2). Следовательно, если построить график этой функции в координатах J - r2, то должна получиться прямая, продолжение которой будет пересекать ось ординат в некоторой точке, соответствующей J0. Такое построение можно сделать приближённо, «на глаз». Однако математические методы обработки результатов наблюдения позволяют сделать такое построение достаточно точным. Наиболее просто это можно сделать с помощью метода наименьших квадратов, вычислив J0 и 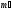 . .Для удобства перепишем формулу (7) в виде: 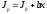 , (8) , (8)где r2 = х и 4m' = b. Метод наименьших квадратов позволяет найти J0 и b: 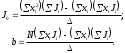 (9) (9)где 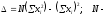 число опытов; Ji - экспериментальное значение момента инерции Jэ, полученное для каждого опыта (табл.1). число опытов; Ji - экспериментальное значение момента инерции Jэ, полученное для каждого опыта (табл.1).Среднее квадратичное отклонение 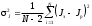 . .Схема установки  Рис.1 1 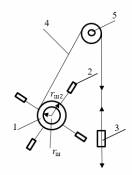 – крестовина; 2 – грузы; 3 – груз, массой m; 4 – нить; 5 – блок. – крестовина; 2 – грузы; 3 – груз, массой m; 4 – нить; 5 – блок. Основные расчётные формулы 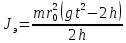 , где , где 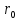 – радиус шкива, m – масса груза, h – путь, пройденный грузом. – радиус шкива, m – масса груза, h – путь, пройденный грузом.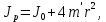 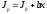 , где , где 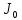 – момент инерции крестовины без грузов. – момент инерции крестовины без грузов.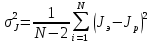 , где , где 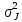 – среднее квадратичное отклонение. – среднее квадратичное отклонение. Формула для расчёта погрешности косвенных измерений 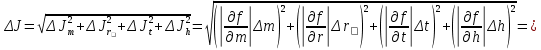 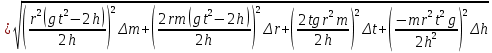 Таблицы Таблица 1. Результаты эксперимента
Таблица 2. Обработка результатов эксперимента
Вычисления Среднее время: 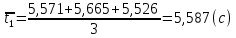 Момент инерции экспериментальный: 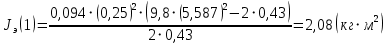 Момент инерции рассчитанный: 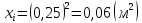 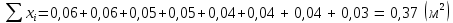 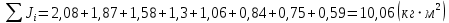 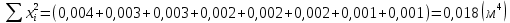 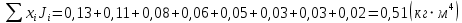 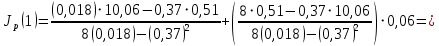 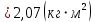 Вычисление среднего квадратичного отклонения: 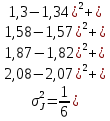 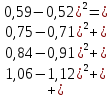 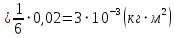 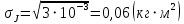 Вычисление погрешностей косвенных измерений 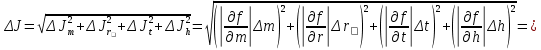 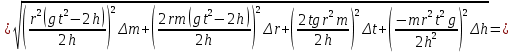 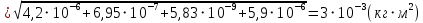 Графический материал 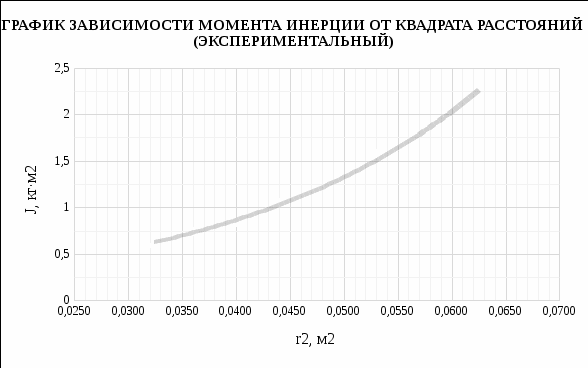 Для сравнения построим график функции в координатах J – r2, полученный методом наименьших квадратов. 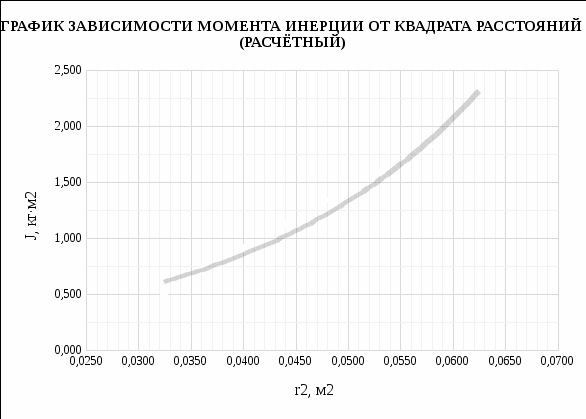 Вывод В ходе выполнения лабораторной работы были получены значения момента инерции с помощью маятника Обербека. Было установлено, что при уменьшении квадрата расстояния от центра грузов до центра масс крестовины момент инерции уменьшается прямо пропорционально времени движения. Значения момента инерции были получены двумя способами: экспериментальным и расчётно-теоретическим. Сравнение, в ходе которого было подтверждено значение среднего квадратичного отклонения, равняющееся 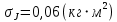 , показало, что вычисления в рамках данных двух способов имеют незначительные различия. Следовательно, можно утверждать, что измерения в рамках данной работы проведены с относительной точностью. , показало, что вычисления в рамках данных двух способов имеют незначительные различия. Следовательно, можно утверждать, что измерения в рамках данной работы проведены с относительной точностью. |