лекция. Определение производной. Производная сложной функции. ЭВМ 328. Определение производной. Производная сложной функции

• Название: Определение производной. Производная сложной функции
• Анкор: лекция
• Дата: 05.05.2022
• Размер: 1.31 Mb.
• Имя файла: Определение производной. Производная сложной функции. ЭВМ 328.docx
• Тип: Документы; #513961

Тема: Определение производной. Производная сложной функции.

1. 
   Определение производной
   

Определение: Производной функции f(x) (f'(x₀)) в точке x₀  называется число, к которому стремится разностное отношение  , стремящемся к нулю.

Производные элементарных функций.



Правила дифференцирования.

Если у функций  f(x) и  g(x) существуют производные, то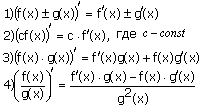



Производная сложной функции:



Геометрический смысл производной. Производная в точке x₀ равна угловому коэффициенту касательной к графику функции  y=f(x) в этой точке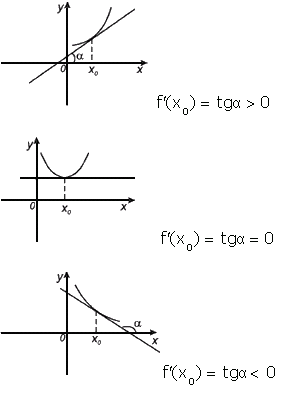



Уравнение касательной к графику функции y=f(x) в точке x₀ :



Физический смысл производной.

Если точка движется вдоль оси х и ее координата изменяется по закону  x(t), то мгновенная скорость точки:

2. 
   Производная сложной функции
   

Что такое сложная функция?

Представь, что ты переезжаешь в другую квартиру и поэтому собираешь вещи в большие коробки. Пусть надо собрать какие-нибудь мелкие предметы, например, школьные письменные принадлежности. Если просто скидать их в огромную коробку, то они затеряются среди других вещей. Чтобы этого избежать, ты сначала кладешь их, например, в пакет, который затем укладываешь в большую коробку, после чего ее запечатываешь. Этот "сложнейший" процесс представлен на схеме ниже:



Казалось бы, причем здесь математика? Да притом, что сложная функция формируется ТОЧНО ТАКИМ ЖЕ способом! Только «упаковываем» мы не тетради и ручки, а xx, при этом «пакетами» и «коробками» служат разные функции.

Например, возьмем x и «запакуем» его в функцию косинуса:



В результате получим, ясное дело, cosxcos⁡⁡x. Это наш «пакет с вещами». А теперь кладем его в «коробку» - запаковываем, например, в кубическую функцию.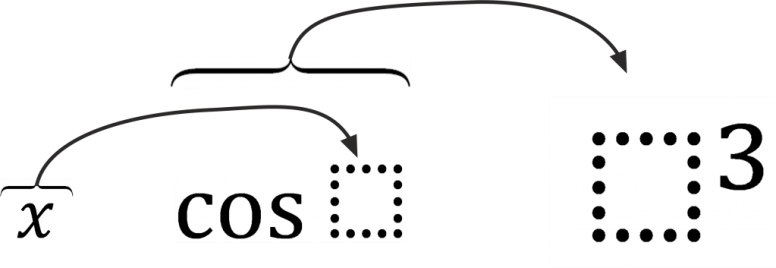



Что получится в итоге? Да, верно, будет «пакет с вещами в коробке», то есть «косинус икса в кубе».



Получившаяся конструкция и есть сложная функция. Она отличается от простой тем, что к одному иксу применяется НЕСКОЛЬКО «воздействий» (упаковок) подряд и получается как бы «функция от функции» - «упаковка в упаковке».

В школьном курсе видов этих самых «упаковок» совсем мало, всего четыре :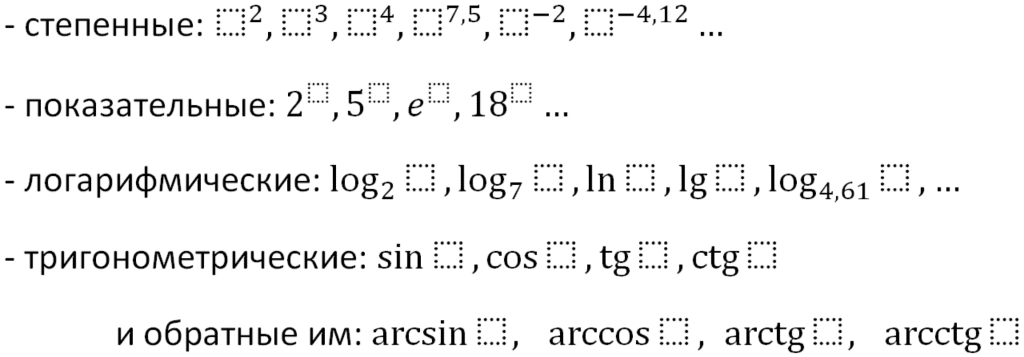



Давай теперь «упакуем» икс сначала в показательную функцию с основанием 7, а потом в тригонометрическую функцию тангенс. Получим:

x→7x→tg(7x)x→7x→tg⁡(7x)

А теперь «упакуем» икс два раза в тригонометрические функции, сначала в синус, а потом в котангенс:

x→sinx→ctg(sinx)x→sin⁡x→ctg⁡(sin⁡x)

Напиши теперь сам функции, где икс:

 - сначала «упаковывается» в косинус, а потом в показательную функцию с основанием 33;

   - сначала в пятую степень, а затем в тангенс;

   - сначала в логарифм по основанию 44, затем в степень −2−2. 

Ответы на это задание посмотри в конце статьи.
А можем ли мы «упаковать» икс не два, а три раза? Да, без проблем! И четыре, и пять, и двадцать пять раз. Вот, например, функция, в которой икс «упакован» 44 раза:

y=5log2sin(x4)y=5log2⁡⁡sin⁡⁡(x4)

«Распаковка» сложной функции

Разматывать последовательность надо В ОБРАТНОМ ПОРЯДКЕ. И тут подсказка как это делать проще: сразу смотри на икс. Разберем несколько примеров.

Например, вот такая функция: y=tg(log2x)y=tg⁡(log2⁡⁡x). Смотрим на икс – что с ним происходит сначала? Берется логарифм от него. А потом? Берется тангенс от результата. Вот и последовательность будет такая же:

x→log2x→tg(log2x)x→log2⁡⁡x→tg⁡(log2⁡⁡x)

Еще пример: y=cos(x3)y=cos⁡⁡(x3). Анализируем – сначала икс возвели в куб, а потом от результата взяли косинус. Значит, последовательность будет: x→x3→cos(x3)x→x3→cos⁡⁡(x3). Обрати внимание, функция вроде бы похожа на самую первую (там, где с картинками). Но это совсем другая функция: здесь в кубе икс (то есть cos(x⋅x⋅x))cos⁡⁡(x·x·x)), а там в кубе косинус xx (то есть, cosx⋅cosx⋅cosxcos⁡⁡x·cos⁡⁡x·cos⁡⁡x). Эта разница возникает из-за разных последовательностей «упаковки».

Последний пример (с важной информацией в нем): y=sin(2x+5)y=sin⁡⁡(2x+5). Понятно, что здесь сначала сделали арифметические действия с иксом, потом от результата взяли синус: x→2x+5→sin(2x+5)x→2x+5→sin⁡⁡(2x+5). И это важный момент: несмотря на то, что арифметические действия функциями сами по себе не являются, здесь они тоже выступают как способ «упаковки». Давай немного углубимся в эту тонкость.

Как я уже говорилось выше, в простых функциях икс «упаковывается» один раз, а в сложных - два и более. При этом любая комбинация простых функций (то есть их сумма, разность, умножение или деление) - тоже простая функция. Например, x7x7 – простая функция и ctgxctgx - тоже. Значит и все их комбинации являются простыми функциями:

x7+ctgxx7+ctgx - простая,
x7⋅ctgxx7·ctgx – простая,
x7ctgxx7ctgx – простая и т.д.

Однако если к такой комбинации применить еще одну функцию – будет уже сложная функция, так как «упаковок» станет две. Смотри схему:


Напиши последовательность «заворачивания» функций:

   y=cos(sinx)y=cos⁡(sin⁡x)

   y=5x7y=5x7

   y=arctg11xy=arctg⁡11x

   y=log2(1+x)y=log2⁡(1+x)

Внутренняя и внешняя функции

Зачем же нам нужно разбираться во вложенности функций? Что нам это дает? Дело в том, что без такого анализа мы не сможем надежно находить производные разобранных выше функций.

И для того, чтобы двигаться дальше, нам будут нужны еще два понятия: внутренняя и внешняя функции. Это очень простая вещь, более того, на самом деле мы их уже разобрали выше: если вспомнить нашу аналогию в самом начале, то внутренняя функция - это «пакет», а внешняя – это «коробка». Т.е. то, во что икс «заворачивают» сначала – это внутренняя функция, а то, во что «заворачивают» внутреннюю – уже внешняя. Ну, понятно почему – она ж снаружи, значит внешняя.

Вот в этом примере: y=tg(log2x)y=tg⁡(log2⁡x), функция log2xlog2⁡⁡x – внутренняя, а 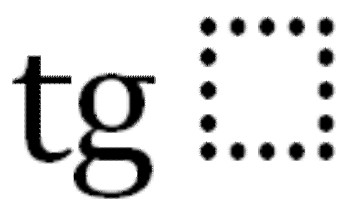  - внешняя.

А в этом: y=cos(x3+2x+1)y=cos⁡⁡(x3+2x+1),   x3+2x+1x3+2x+1 - внутренняя,  а 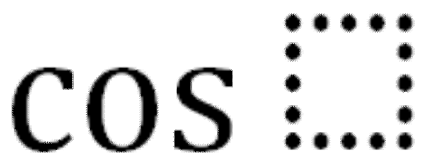  - внешняя.

Выполни последнюю практику анализа сложных функций, и перейдем, наконец, к тому, ради чего всё затевалось - будем находить производные сложных функций:

Заполни пропуски в таблице:

Производная сложной функции

Браво нам, мы всё ж таки добрались до «босса» этой темы – собственно, производной сложной функции, а конкретно, до той самой ужасной формулы из начала статьи.☺

(f(g(x)))′=f′(g(x))⋅g′(x)(f(g(x)))′=f′(g(x))⋅g′(x)

Формула эта читается так:

Производная сложной функции равна произведению производной внешней функции по неизменной внутренней на производную внутренней функции.

И сразу смотри схему разбора "по словам" чтобы понимать, что к чему относиться:



Надеюсь, термины «производная» и «произведение» затруднений не вызывают. «Сложную функцию» - мы уже разобрали. Загвоздка в «производной внешней функции по неизменной внутренней». Что это такое?

Ответ: это обычная производная внешней функции, при которой изменяется только внешняя функция, а внутренняя остается такой же. Все равно непонятно? Рассмотрим на примере.

Пусть у нас есть функция y=sin(x3)y=sin⁡⁡(x3). Понятно, что внутренняя функция здесь x3x3, а внешняя   . Найдем теперь производную внешней по неизменной внутренней.

Из таблицы производных мы знаем, что производная синуса икс есть косинус икс (sinx)′=cosx(sin⁡⁡x)′=cos⁡⁡x.

Тогда производная внешней функции по неизменной внутренней для нашего случая будет cos(x3)cos⁡⁡(x3). То есть, мы взяли ее как обычную производную синуса, а содержимое синуса (внутреннюю функцию) просто скопировали в полученную производную (косинус), ничего в ней не меняя.

Таким образом, на данный момент имеем: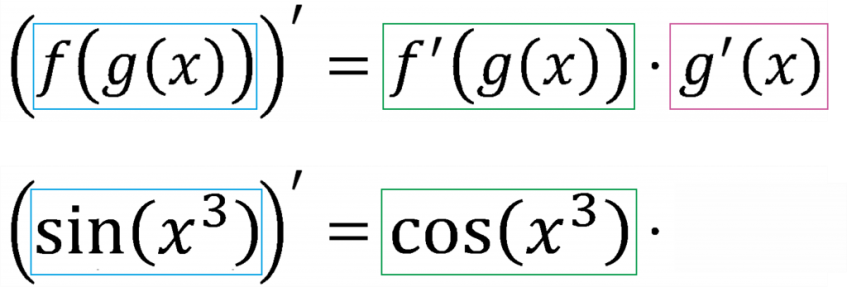



Осталась «производная внутренней функции». Ну, это совсем легко – обычная производная от внутренней функции, при этом внешняя не влияет вообще никак. В нашем примере, производная от x3x3.

(x3)′=3x2(x3)′=3x2

Все, теперь можем писать ответ: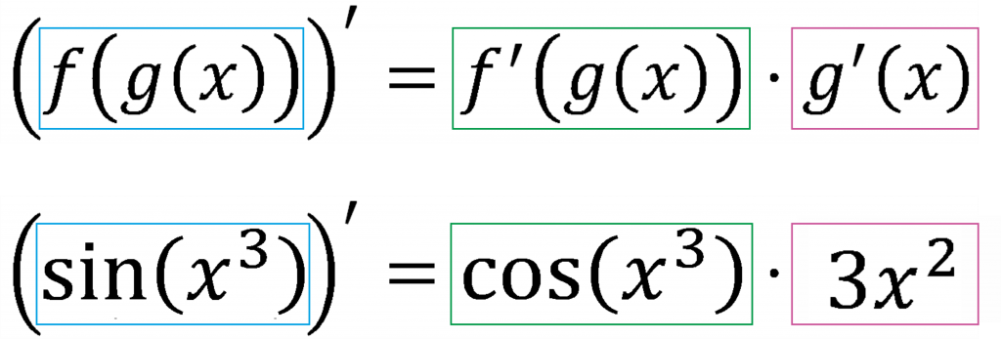



Вот так. Давай еще один пример разберем.

Пусть надо найти производную функции y=(sinx)3y=(sin⁡⁡x)3.

Анализируем. Последовательность «заворачивания» у нас такая: x→sinx→(sinx)3x→sin⁡⁡x→(sin⁡⁡x)3. Значит, в данном примере внутренняя функция это sinxsin⁡⁡x, а внешняя  .

Производная внешней по внутренней – это производная куба (содержимое куба при этом не меняется). Так как 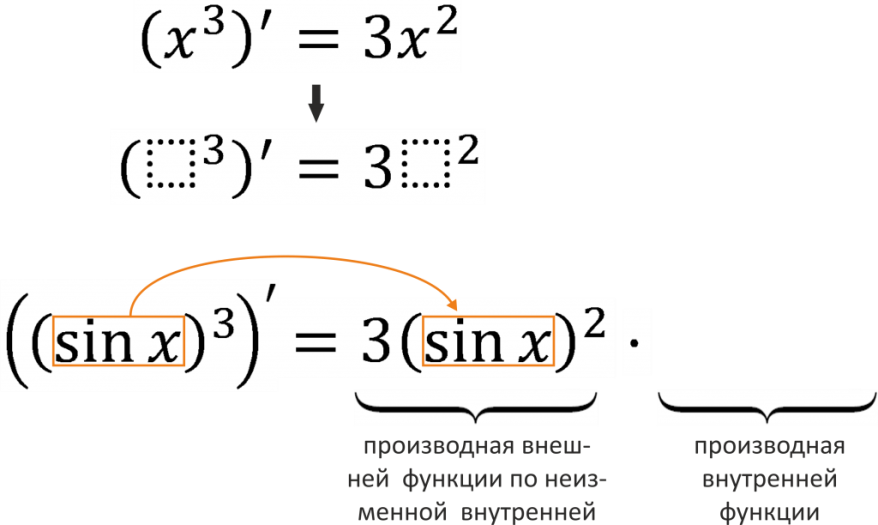 , а в нашем случае в куб «завернут» sinxsin⁡⁡x, то производная внешней будет 3(sinx)23(sin⁡⁡x)2. То есть, имеем:



Ну, а производная внутренней – это просто производная синуса икс, то есть косинус икс.

В итоге, имеем:

y′=((sinx)3)′=3(sinx)2⋅(sinx)′=3(sinx)2⋅cosxy′=((sin⁡⁡x)3)′=3(sin⁡⁡x)2·(sin⁡⁡x)′=3(sin⁡⁡x)2·cos⁡⁡x

Еще один пример с разбором.

Пример. Найти производную сложной функции y=ln(x2−x)y=ln⁡(x2−x).

Разбираем вложенность функций: x→x2−x→ln(x2−x)x→x2−x→ln⁡⁡(x2−x).

Внутренняя: x2−xx2−x.  Внешняя:  .  

Из таблицы производных знаем: .

То есть производная внешней по внутренней будет: ln(x2−x)′=ln⁡⁡(x2−x)′= 1x2−x1x2−x.
Производная внутренней: (x2−x)′=(x2)′−(x)′=2x−1(x2−x)′=(x2)′−(x)′=2x−1.

В итоге, согласно большой и страшной формуле имеем:

y′=(ln(x2−x))′=y′=(ln⁡⁡(x2−x))′=1x2−x1x2−x⋅(2x−1)·(2x−1)

Ну и напоследок можно немного «причесать» ответ, чтоб никто не докопался:

y′=(ln(x2−x))′=y′=(ln⁡⁡(x2−x))′=1x2−x1x2−x⋅(2x−1)=·(2x−1)=2x−1x2−x2x−1x2−x

Готово.

Пример. Найти производную сложной функции y=sin(cosx)y=sin⁡⁡(cos⁡⁡x).

Вложенность функций: x→cosx→sin(cosx)x→cos⁡⁡x→sin⁡⁡(cos⁡⁡x)

Внутренняя: cosxcos⁡⁡x    Внешняя:

Производная внешней по внутренней: sin(cosx)′=coscosxsin⁡⁡(cos⁡⁡x)′=cos⁡⁡cos⁡⁡x

Производная внутренней: (cosx)′=−sinx(cos⁡⁡x)′=−sin⁡⁡x

Имеем: y′=(sin(cosx))′=coscosx⋅(−sinx)=−coscosx⋅sinxy′=(sin⁡⁡(cos⁡⁡x))′=cos⁡⁡cos⁡⁡x·(−sin⁡⁡x)=−cos⁡⁡cos⁡⁡x·sin⁡⁡x

Замечание: Обрати внимание, что заменить запись coscosxcos⁡⁡cos⁡⁡x на cos2xcos2⁡⁡x НЕЛЬЗЯ, так как cos2xcos2⁡⁡x - это комбинация простых функций cos2x=cosx⋅cosxcos2⁡⁡x=cos⁡⁡x·cos⁡⁡x, а coscosxcos⁡⁡cos⁡⁡x – сложная функция: косинус от косинуса икс. Это абсолютно разные функции.

Еще пример с важным замечанием в нем.

Пример. Найти производную сложной функции y=√x6y=x6

Вложенность функций: x→x6→√x6x→x6→x6

Внутренняя: x6x6      Внешняя: 

Производная внешней по внутренней: √x6′=x6′=12√x612x6

Производная внутренней: (x6)′=6x5(x6)′=6x5

Имеем: (√x6)′=(x6)′=12√x612x6⋅6x5·6x5

И теперь упростим ответ. Вспомним свойство корня: b√xa=xabxab=xab. Тогда √x6=x62=x3x6=x62=x3. С учетом этого получаем:

y′=(√x6)′=y′=(x6)′=12√x612x6⋅6x5=·6x5=12x312x3⋅6x5=·6x5=6x52x36x52x3=3x2=3x2

Всё. А теперь, собственно, важное замечание:

Тот же самый ответ, но значительно меньшими усилиями мы могли бы получить, упростив исходную функцию сразу. Воспользуемся тем же свойством корня: b√xa=xabxab=xab. Тогда исходная функция приобретает вид: y=√x6=x62=x3y=x6=x62=x3. А производная куба это практически табличное значение! Готов ответ: y′=(√x6)′=(x3)′=3x2y′=(x6)′=(x3)′=3x2. Немножко проще предыдущего решения, правда ☺? Поэтому прежде чем искать производную, посмотрите, можно ли исходную функцию упростить, чтоб решать было проще.

Рассмотрим пример, где эта идея нам сильно поможет.

Пример. Найти производную сложной функции y=ln(x3)y=ln⁡⁡(x3).

Можно, конечно, рассмотреть вложенность функций: x→x3→ln(x3)x→x3→ln⁡⁡(x3), разобрать на внутреннюю и внешнюю и так далее. Но можно вспомнить свойство логарифма: logabc=c⋅logabloga⁡⁡bc=c·loga⁡⁡b. И тогда функция получается y=ln(x3)=3lnxy=ln⁡⁡(x3)=3ln⁡⁡x. Отлично! Берем производную:

y′=(ln(x3))′=(3lnx)′=3(lnx)′=3⋅y′=(ln⁡⁡(x3))′=(3ln⁡⁡x)′=3(ln⁡⁡x)′=3·1x=3x1x=3x

Теперь задачка посложнее, для продвинутых. Решим пример с тройной вложенностью!

Пример. Найти производную сложной функции y=3sin(x4+1)y=3sin⁡⁡(x4+1).

Вложенность функций: x→x4+1→sin(x4+1)→3sin(x4+1)x→x4+1→sin⁡⁡(x4+1)→3sin⁡⁡(x4+1)

Внутренняя: x4+1x4+1    Средняя:       Внешняя: 

Сначала производная внешней по средней. Вспоминаем таблицу производных: 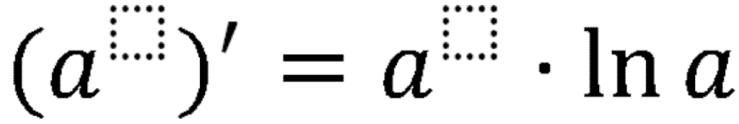 . Значит, в нашем случае будет 3sin(x4+1)⋅ln33sin⁡⁡(x4+1)·ln⁡⁡3.

Хорошо, теперь производная средней по внутренней. По таблице: 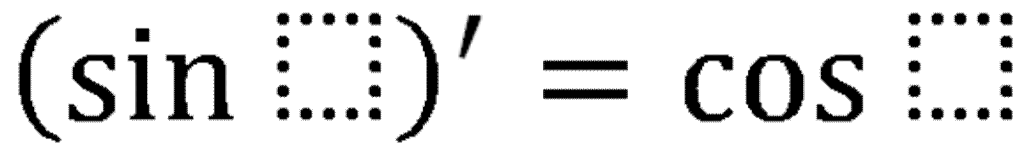 . Значит, мы получим, sin(x4+1)′=cos(x4+1)sin⁡⁡(x4+1)′=cos⁡⁡(x4+1).

И наконец, производная внутренней: (x4+1)′=(x4)′+(1)′=4x3(x4+1)′=(x4)′+(1)′=4x3.

Отлично. Теперь собираем все вместе, перемножая отдельные производные:

(3sin(x4+1))′=3sin(x4+1)⋅ln3⋅cos(x4+1)⋅4x3(3sin⁡⁡(x4+1))′=3sin⁡⁡(x4+1)·ln⁡⁡3·cos⁡⁡(x4+1)·4x3

Готово.

Пример: Найти производную сложной функции y=tg(7x)y=tg⁡(7x).

Разбираем вложенность функций: x→7x→tg(7x)x→7x→tg⁡(7x).

Внутренняя: 7x7x       Внешняя: tg(7x)tg⁡(7x).

Ищем производную самой внешней функции, внутреннюю при этом не трогаем.

Из таблицы производных знаем:  .

То есть, в нашем случае производная внешней по внутренней будет:  1cos2(7x)1cos2⁡⁡(7x).
Теперь ищем производную внутренней. Этой формулой мы уже пользовались, так что сразу пишем ответ: (7x)′=7x⋅ln7(7x)′=7x·ln⁡⁡7.

И перемножаем результаты:

y′=tg(7x)′=y′=tg⁡(7x)′=1cos2(7x)⋅7x⋅ln71cos2⁡(7x)·7x·ln⁡⁡7

И:   y′=(tg(7)x))′=y′=(tg⁡(7)x))′=1cos2(7x)1cos2⁡(7x)⋅7x⋅ln7=·7x·ln⁡⁡7=ln7⋅7xcos2(7x)ln⁡⁡7·7xcos2⁡(7x).

Последний пример. Такие задания в разных вариациях весьма часто дают на контрольных и тестах.

Пример: Найти производную сложной функции y=3√(x5+2x−5)2y=(x5+2x−5)23.

Казалось бы, опять у нас тройная вложенность функций:

x→x5+2x−5→(x5+2x−5)2→3√(x5+2x−5)2x→x5+2x−5→(x5+2x−5)2→(x5+2x−5)23.

Но давай снова воспользуемся свойством корня b√xa=xabxab=xab и преобразуем нашу функцию к виду:

y=3√(x5+2x−5)2=(x5+2x−5)23y=(x5+2x−5)23=(x5+2x−5)23

Вот так. И теперь у нас вложенность двойная: x→x5+2x−5→(x5+2x−5)23x→x5+2x−5→(x5+2x−5)23

При этом функция осталась той же! Удобное свойство, однако. Стоит его запомнить.

Внутренняя функция: x5+2x−5x5+2x−5.    Внешняя:  .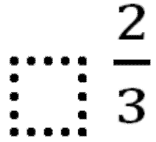

Производная внешней по внутренней. По таблице производных общая формула производной степенной функции: 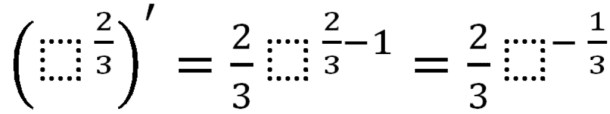   . Получаем:    . Тогда в нашем случае будет: 23(x5+2x−5)−1323(x5+2x−5)−13.

Производная внутренней: (x5+2x−5)′=5x4+2(x5+2x−5)′=5x4+2.

Общий результат: y′=(3√(x5+2x−5)2)′=((x5+2x−5)23)′=23(x5+2x−5)−13⋅(5x4+2)y′=((x5+2x−5)23)′=((x5+2x−5)23)′=23(x5+2x−5)−13·(5x4+2).

В принципе, ответ найден. Вспоминаем свойство отрицательной степени a−n=a−n=1an1an. Получаем:

y′=23(x5+2x−5)−13⋅(5x4+2)=y′=23(x5+2x−5)−13·(5x4+2)=2323⋅·1(x5+2x−5)131(x5+2x−5)13⋅(5x4+2)·(5x4+2)

А теперь применяем свойство корня b√xa=xabxab=xab в обратную сторону. То есть, вот так xab=b√xaxab=xab. В результате имеем:

y′=y′=23231(x5+2x−5)131(x5+2x−5)13⋅(5x4+2)=·(5x4+2)=232313√x5+2x−51x5+2x−53⋅(5x4+2)·(5x4+2)

Ну, и перемножаем дроби.

y′=y′=232313√x5+2x−51x5+2x−53⋅(5x4+2)=·(5x4+2)=2(5x4+2)33√x5+2x−52(5x4+2)3x5+2x−53==10x4+433√x5+2x−510x4+43x5+2x−53

Самостоятельная работа

Найти производные функций:

a. y=ctg(x7)y=ctg⁡(x7)

b. y=ex4+5x3y=ex4+5x3

c. y=√cosxy=cos⁡⁡x

d. y=log55xy=log5⁡⁡5x

e. y=(tgx)3y=(tg⁡x)3

f. y=sin(ln(x2))y=sin⁡⁡(ln⁡⁡(x2))

Ответы ко всем заданиям (вперемежку).

y=tg(x5)y=tg⁡(x5)

y=log−24xy=log4−2⁡⁡x

y=3cosxy=3cos⁡⁡x

x→1+x→log2(1+x)x→1+x→log2⁡⁡(1+x)

x→11x→arctg(11x)x→11x→arctg⁡(11x)

x→x7→5x7x→x7→5x7

x→sinx→cos(sinx)x→sin⁡⁡x→cos⁡⁡(sin⁡⁡x)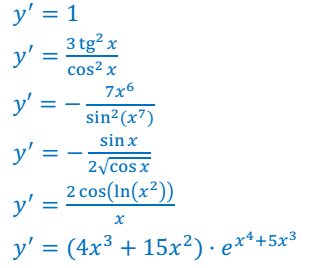