Отчет №2. Определение размера наночастиц по формуле Шеррера
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное автономное образовательное учреждение высшего образования «Уральский Федеральный Университет имени первого Президента России Б.Н. Ельцина» Физико-технологический институт Кафедра «Физических методов и приборов контроля качества» Оценка работы ______ Руководитель: Дорошева И.Б. ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №2 Материалы и методы нанотехнологий по теме: «Определение размера наночастиц по формуле Шеррера» Студент гр. Фт-480009 ___________________ Сорокин В.Д. (подпись, дата) Екатеринбург 2022 Цели работы: Ознакомиться с понятиями: рентгеноструктурный анализ, область когерентного рассеяния,размер и форма наночастиц; Ознакомиться с формулой Шеррера, ознакомиться с понятиями: профиль дифракционных рентгеновских пиков, полная ширина на половине высоты пиков, функция псевдо-Фойгта; Ознакомиться с методом полнопрофильного анализа рентгеновских пиков, Научиться измерять величину уширения дифракционных пиков; Научиться определять средний размер наночастиц по формуле Шеррера. Этапы выполнения работы: - ознакомиться с принципом действия двухкружного рентгеновского дифрактометра Philips X'Pert; −изучить геометрию съемки рентгеновского дифракционного спектра по методу БрэггаБрентано; −подготовить образец и стандарт для съемки спектров на рентгеновском дифрактометре Philips X'Pert; −снять спектры с нанопорошка и стандарта LaB6; −описать отдельные пики спектра функцией псевдо-Фойгта; −определить функцию разрешения прибора с помощью стандарта; −определить уширение пиков на спектрах нанопорошковых образцов; −определить размеры наночастиц (областей когерентного рассеяния) по формуле Шеррера. Теоретическая часть: Обработка ренгеноструктурных данных: Для полнопрофильного описания дифракционных рентгеновских рефлексов используется функция псевдо-Фойгта: 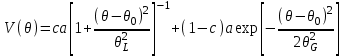 , (1) , (1)где с - относительный вклад функции Лоренца в общую интенсивность рефлекса; L и G - параметры распределений Лоренца и Гаусса, соответственно; а - нормирующий множитель интенсивности; 0 – положение максимума функции и рефлекса. Для сьемки рентгеновского спектра использовалось излучение с двумя длинами волн 1 и 2, поэтому каждый рефлекс давал дублет в спектре. В связи с этим для описания одного рефлекса использовались две функции псевдо-Фойгта (1). В соответствии с законом Вульфа-Брегга положения максимумов 0,1 и 0,2 функций псевдо-Фойгта были жестко связаны через межплоскостное расстояние, соответствующее данному рефлексу, по формуле 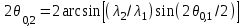 . Интенсивность Cu-K2 линии в дублете составляла 0.497 от интенсивности Cu-K1 линии. Численные значения параметров а, c, 0 , L и G для каждого рефлекса находили с помощью аппроксимации экспериментального спектра методом наименьших квадратов. . Интенсивность Cu-K2 линии в дублете составляла 0.497 от интенсивности Cu-K1 линии. Численные значения параметров а, c, 0 , L и G для каждого рефлекса находили с помощью аппроксимации экспериментального спектра методом наименьших квадратов. На экспериментальных спектрах порошков после размола наблюдается значительное уширение дифракционных пиков. Уширение пиков в нанопорошках может быть связано с нарушением трансляционной симметрии кристаллической структуры, а также некоторых элементов точечной симметрии, вследствие малого размера частиц порошка. Кроме того, следует учесть вклад от инструментального уширения дифракционных пиков, так как этот вклад существенен особенно для крупных нанопорошков. Практическая часть: Инструментальную ширину, т.е. функцию разрешения дифрактометра, определяем на стандартном порошке гексаборида лантана LaB6. По представленным нам данным строим зависимость интенсивности от угла рассеяния 2θ, I = f (2θ) в графическом программном пакете SigmaPlot, график рентгенограммы представлен на рисунке 1. 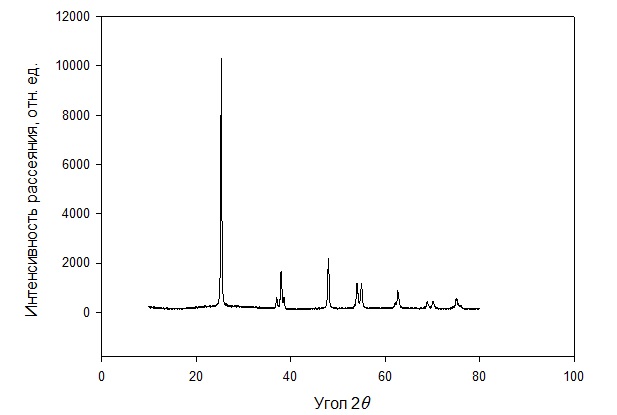 Рисунок 1 – Рентгенограмма для стандартного порошка и исследуемого вещества LaB6 Теперь построим каждый пик рентгенограммы на отдельном графике. Для этого выделим данные для одного пика и скопируем в отдельные столбцы программы. В качестве примера построим первый пик рентгенограммы, представленный на рисунке 2. Далее по графику приблизительно определим параметры первого пика: а – высота пика (разность максимума и уровня фона), b – ширина пика на половине его высоты, х0 (град.) – значение 2θ, соответствующее максимуму пика, bg – уровень фона. Все данные приведены в таблице 1 Таблица 1 – Приблизительные параметры пиков
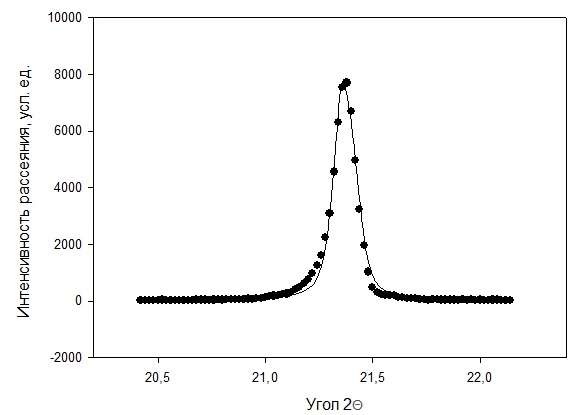 Рисунок 2 – Рентгенограмма первого пика Теперь описываем пик, с найденными значениями параметров a, b, c, 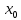 . Затем записываем новые значения a, b, c, . Затем записываем новые значения a, b, c, 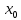 в новый лист и строим функцию Псевдо-Фойгта с использованием рассчитанной программой интенсивности. Повторяем описанные действия для всех пиков рентгенограммы. в новый лист и строим функцию Псевдо-Фойгта с использованием рассчитанной программой интенсивности. Повторяем описанные действия для всех пиков рентгенограммы.Характеристики 1 пика: 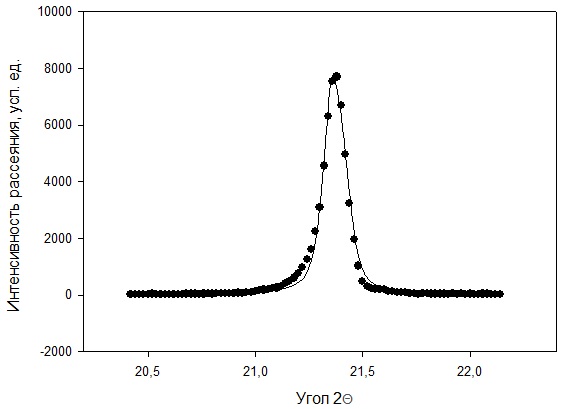 Рисунок 1 – Аппроксимированный первый пик 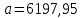    Характеристики 2 пика: 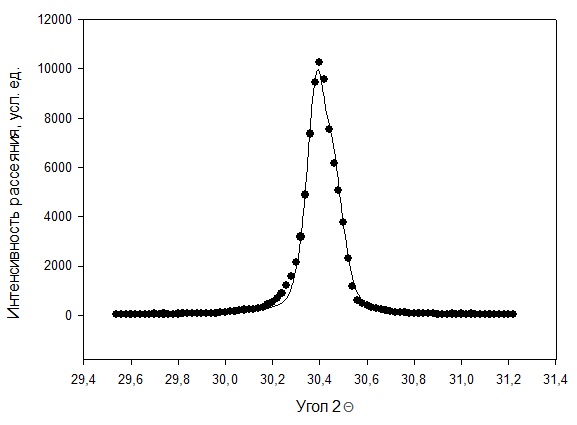 Рисунок 2 - Аппроксимированный второй пик 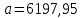 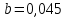 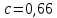 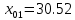 Характеристики 3 пика: 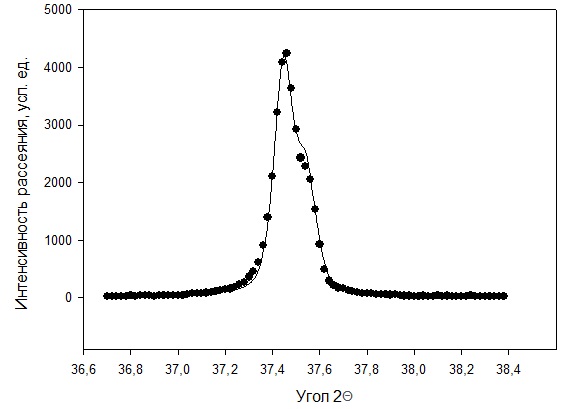 Характеристики 4 пика: 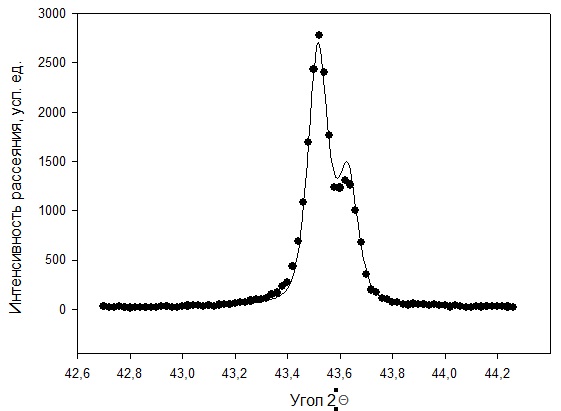 Характеристики 5 пика: 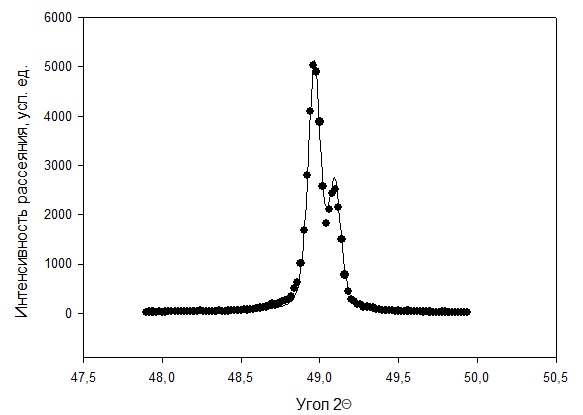 Характеристики 6 пика: 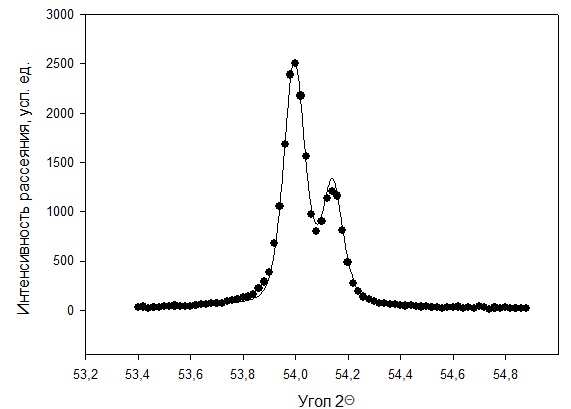 Характеристики 7 пика: 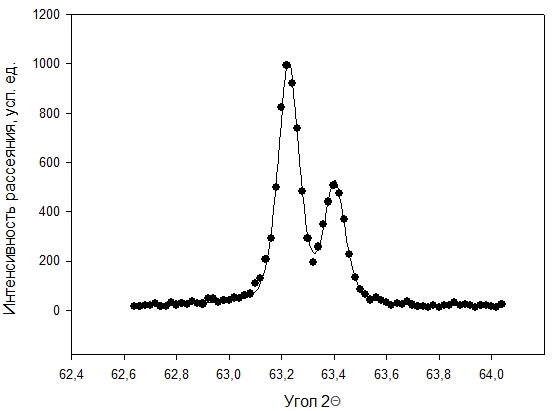 Характеристики 8 пика: 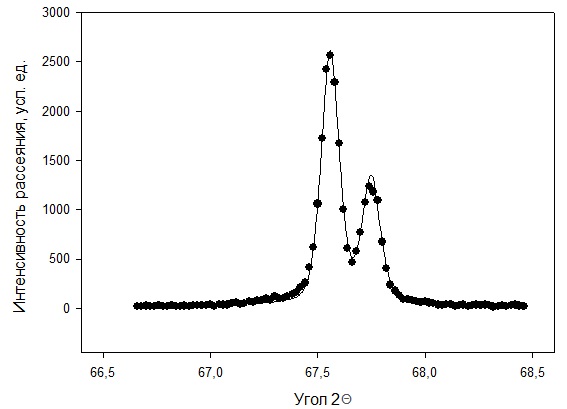 Характеристики 9 пика: 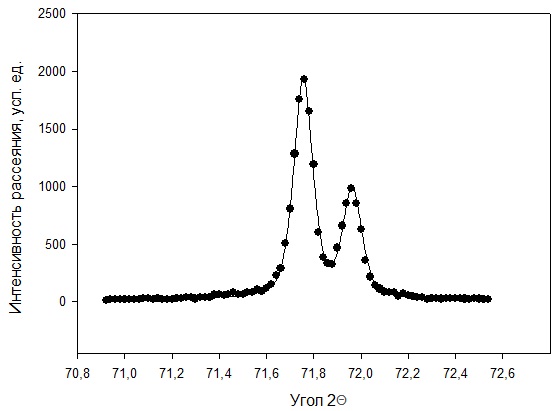 Характеристики 10 пика: 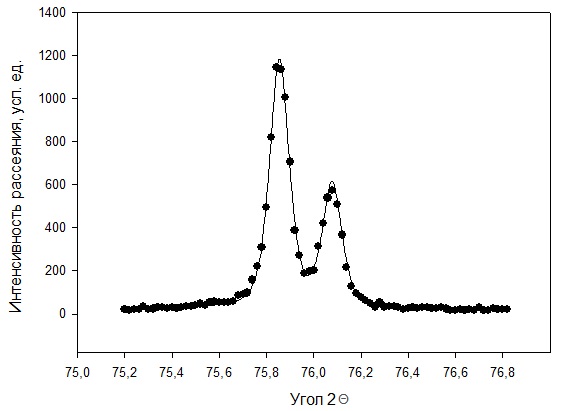 Характеристики 11 пика: 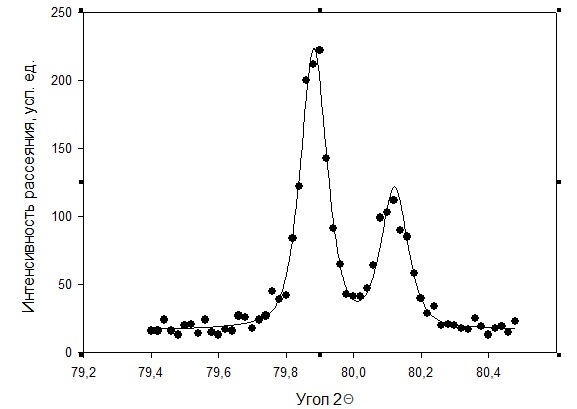 Характеристики 12 пика: 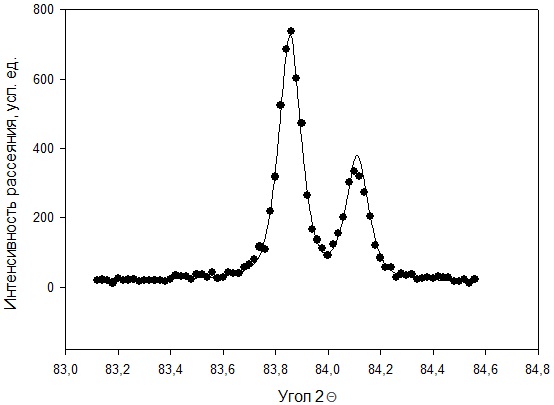 Характеристики 13 пика: 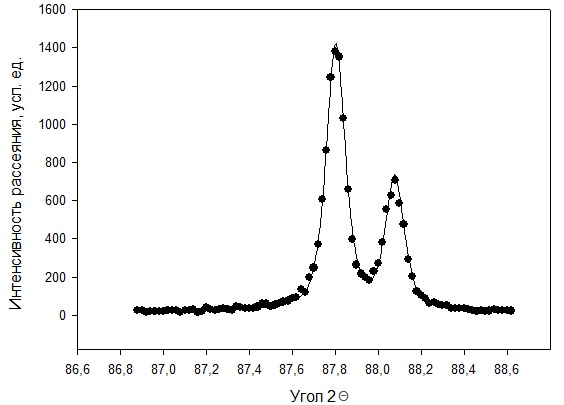 Характеристики 14 пика: 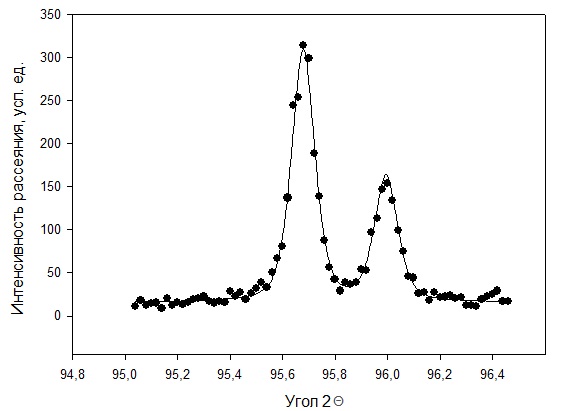 Характеристики 15 пика: 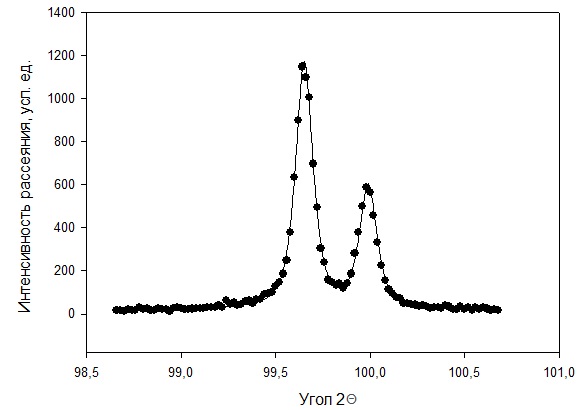 Характеристики 16 пика: 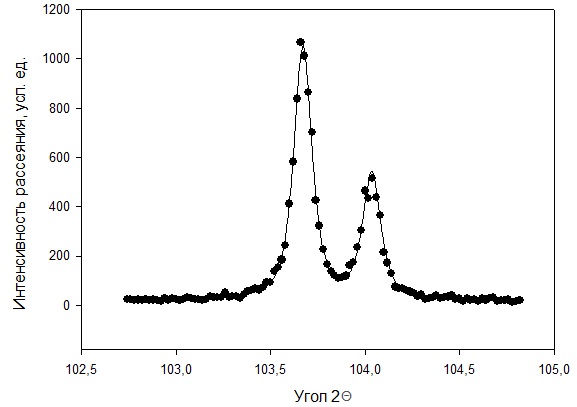 Характеристики 17 пика: 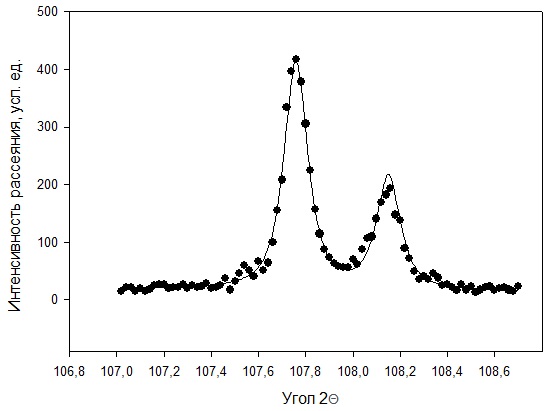 Характеристики 18 пика: 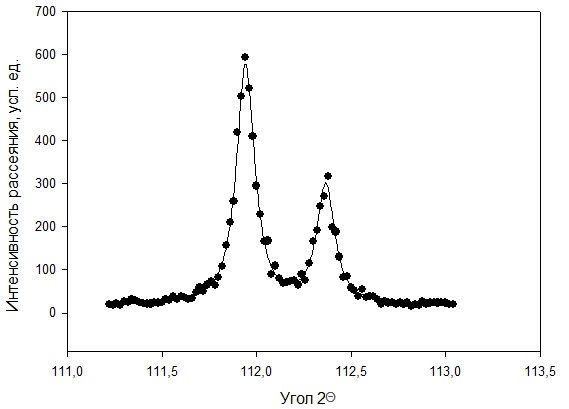 Характеристики 19 пика: 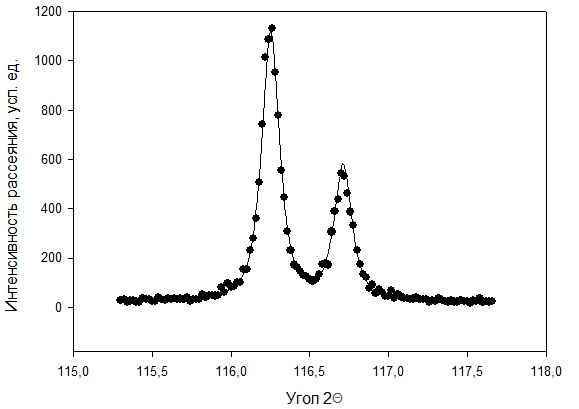 Описав каждый пик рентгенограммы, я создал таблицу с параметрами a, b, c, x01, представленною на рисунке 24. 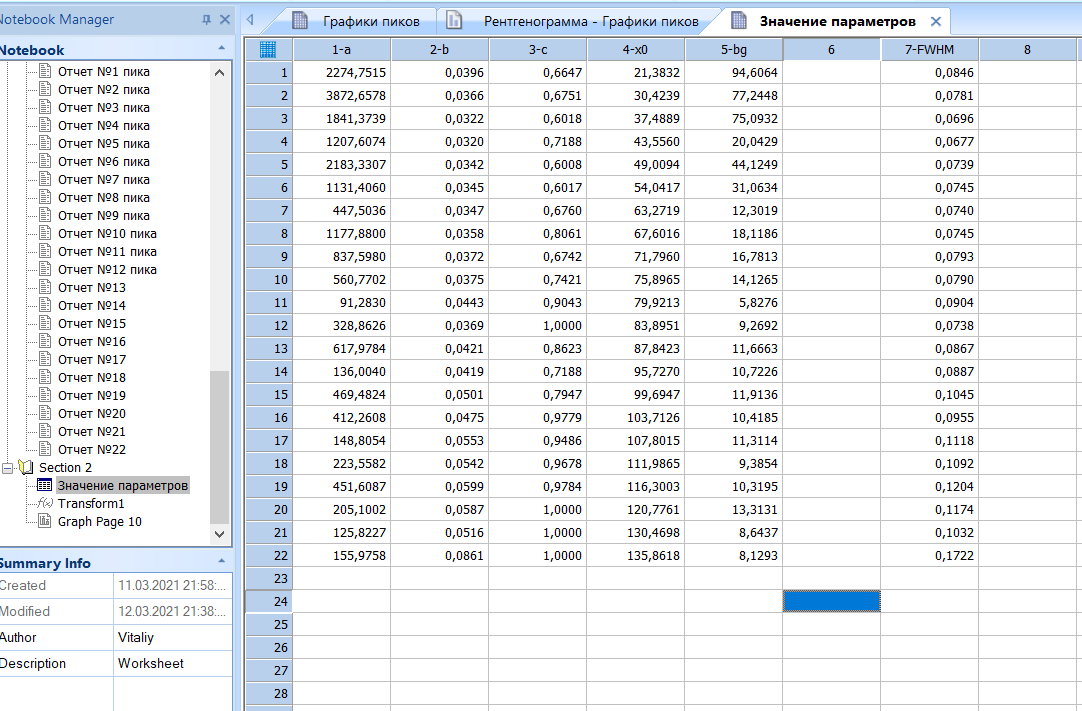 Рисунок 24 – Параметры a, b, c, x01 Далее строим график x01 от FWHM, представленный на рисунке 25. 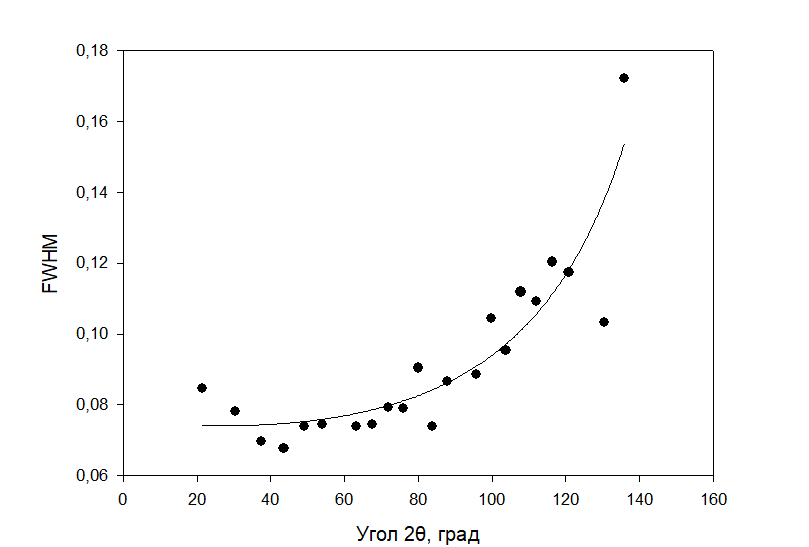 Рисунок 25 – Зависимость FWHM от угла тетэ Теперь мы определили функцию разрешения дифрактометра и определили параметры u, v, w, которые равны следующим значениям: u = 0,0036 v = -0,0017 w = 0,0057 Вывод: В ходе выполнения лабораторной работы № 2, я описал профиль дифракционных рентгеновских пиков порошков и стандарта функцией псевдо-Фойгта и определить уширения пиков на спектрах нанопорошковых образцов. Также определил инструментальную ширину, т.е. функцию разрешения дифрактометра в специальном дифракционном эксперименте на стандартном порошке гексаборида LaB6. |
