Определение скорости распространения звука в воздухе
 Скачать 148.5 Kb.
|
|
Определение скорости распространения звука в воздухе Цель работы: определение скорости распространения звуковых колебаний в воздухе при данной температуре методом стоячих волн. Приборы и принадлежности: установка акустического резонанса, электронный осциллограф, звуковой генератор. Исследуемые закономерности Звуковые колебания в газе представляют собой периодическое чередование сжатий и разрежений, распространяющихся со скоростью, зависящих от свойств воздуха. Газы, в отличие от твердых тел, не обладают деформацией сдвига, поэтому в них возникают только продольные волны. Продольные волны обусловлены объемной деформацией. Если сжатие происходит быстро, то выделяющееся при этом тепло не успевает распространится в соседние слои. Сжатие без отвода тепла называется адиабатическим; в этом случае скорость распространения звука рассчитывают по формуле  , (1)где  - отношение теплоемкостей газа при изобарическом и изохорическом процессах (для воздуха  );  и  - соответственно, средние значения давления и плотности во всем объеме.Соотношение (1) может быть преобразовано с учетом уравнения состояния идеального газа:  где R – газовая постоянная; Т – температура;  - молярная масса газа ( для воздуха  кг/моль).Удобным методом измерения скорости звуковых волн является метод, основанный на измерении длины волны  стоячих звуковых волн. Если измерена и известна частота  возбуждаемых звуковых волн, то Стоячие звуковые волны возникают при интерференции падающей и отраженной волн. Точки, в которых амплитуда колебаний максимальна, называют пучностями стоячей волны. Точки, в которых амплитуда колебаний равна нулю, называются узлами стоячей волны. Явление резонанса наблюдается в том случае, если длина резонатора  , в котором устанавливается стоячая волн, равна целому числу полуволн: , n = 1, 2, 3,… Явление резонанса четко выражено в том случае, если затухание мало. В данном случае затухание обусловлено неполным отражением волн и потерями на излучение из резонатора в окружающую среду, оно невелико, и можно считать, что период колебаний  . Характеристикой убыли энергии при затухании служит добротность системы Знаменатель представляет убыль энергии за период, отсчитываемый от момента времени t. Добротность можно рассчитать также по следующей формуле:  , где  - число колебаний за время, в течение которого амплитуд колебаний уменьшается в е раз.Небольшая расстройка (т.е. отклонение) частоты относительно резонансной позволяет наблюдать изменение амплитуды колебаний в соответствии с амплитудно-частотной характеристикой резонатора:  где 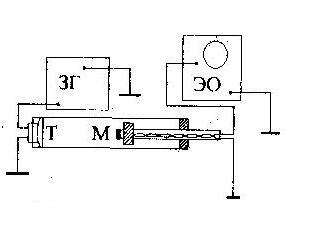 и  - амплитуда и частота при резонансе;  - ширина резонансной кривой, которая определяется как разность частот, при которых амплитуда  . Метод измерений. Работа выполняется на установке, схема которой приведена на рисунке. На одном конце кварцевой трубы находится телефон Т, являющийся источником звука. Телефон соединен звуковым генератором ЗГ. Колебания мембраны телефона создают периодические сгущения и разрежения в прилегающем к ней слое воздуха, возбуждая акустическую волну.Внутри трубы перемещается поршень с вмонтированным в него приемником – микрофоном М. Микрофон принимает звуковые колебания, преобразует их в электрические и передает на вход Y электронного осциллографа ЭО. На экране осциллографа возникает синусоидальный сигнал, амплитуда которого различна в зависимости от частоты колебаний и длины резонатора. При выполнении условия (1.4) наступает резонанс, при котором амплитуда наблюдаемых колебаний максимальна. Настройка на резонанс может быть осуществлена любо изменением длины воздушного столба в трубе (перемещением поршня), либо изменением частоты колебаний генератора. В работе используется первый способ. Обработка результатов наблюдений
 , при  1000Гц
  334 м/с
  1,838
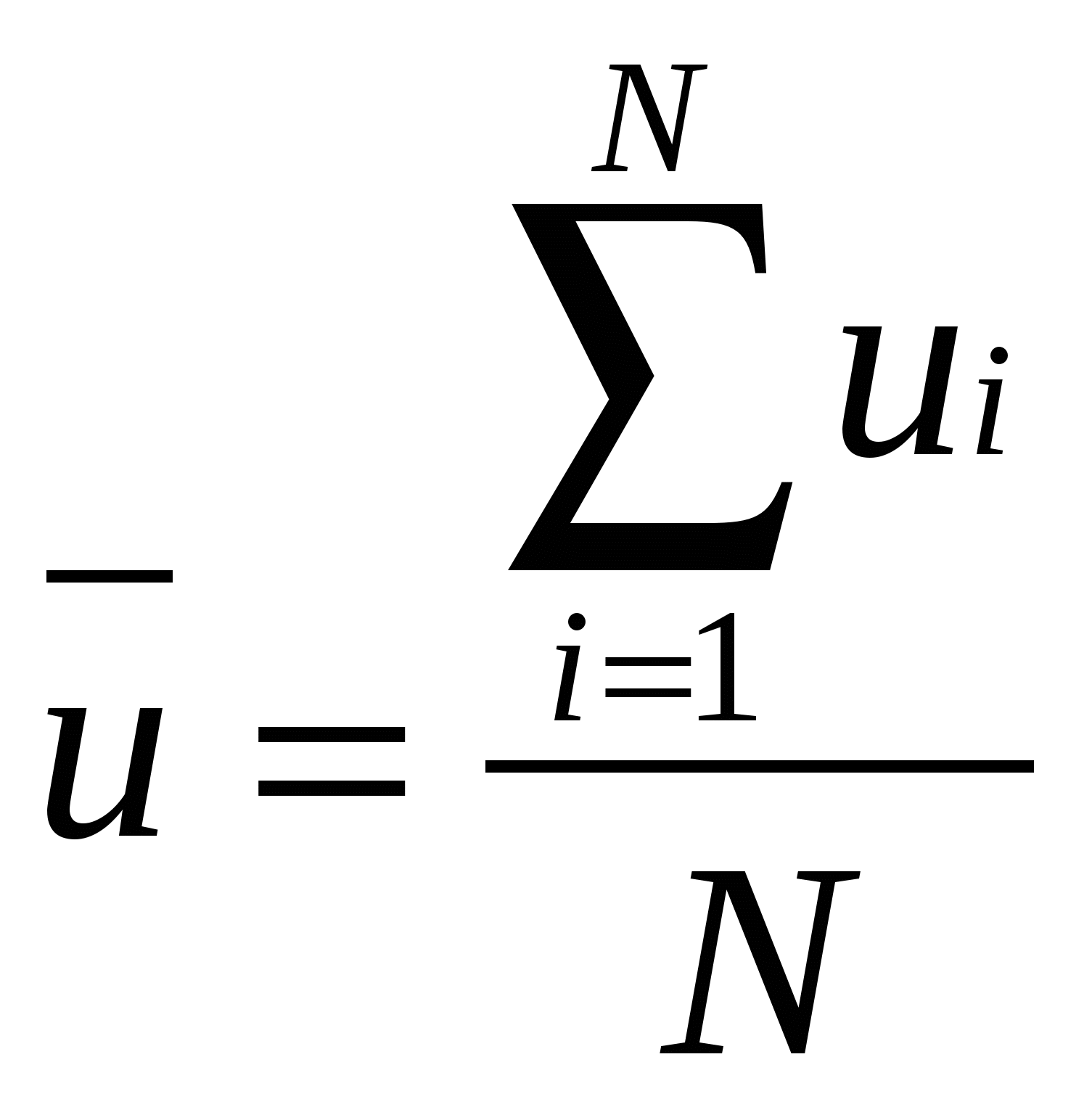
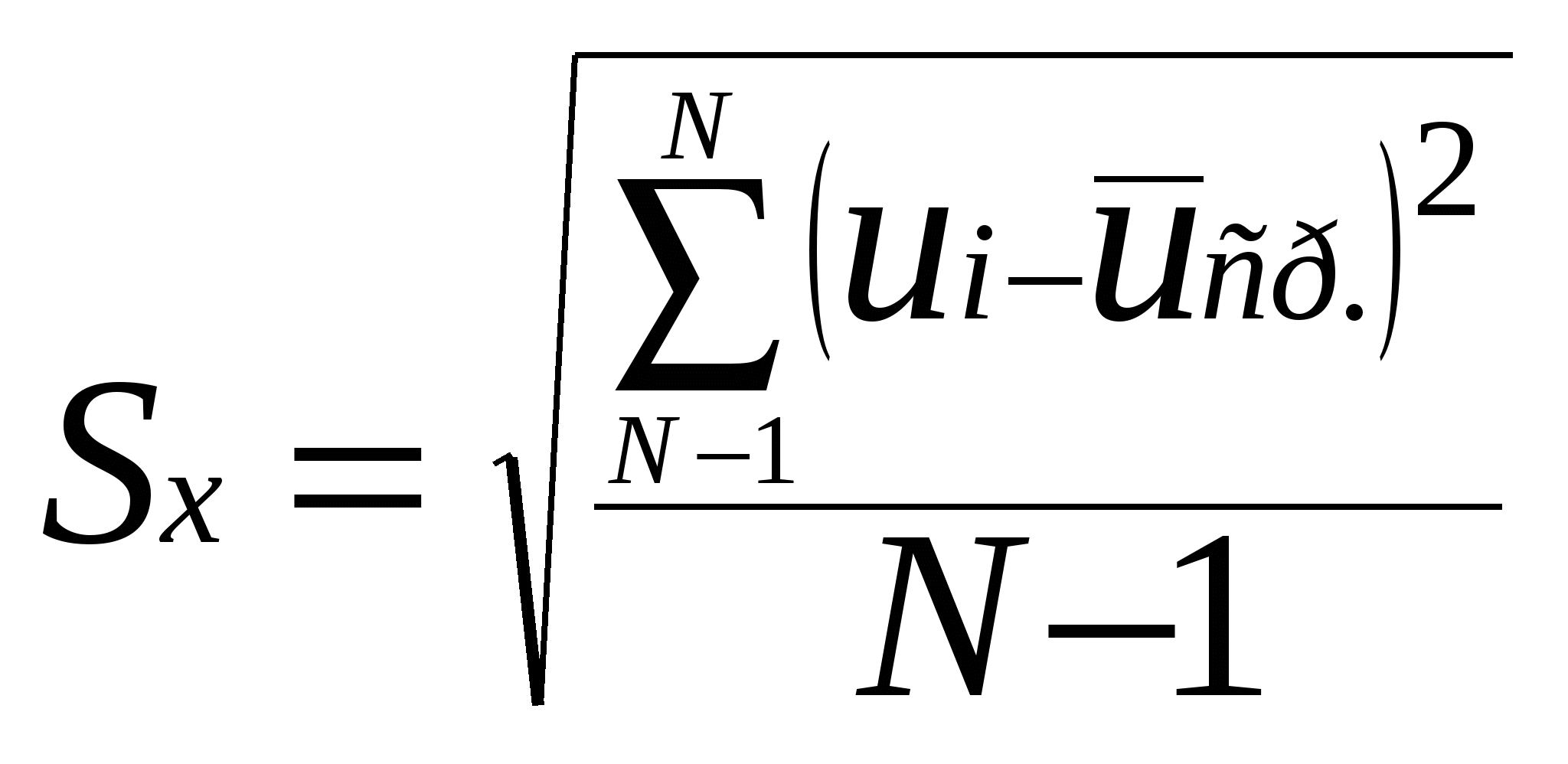
  p = 95%3  3.492Следовательно, результат – не промах
  = =0,336 = 0,336
  
 
 
  при p= 95%
= 344,01 (м/с)Вывод: в ходе работы была определена скорость распространения звуковых колебаний в воздухе при данной температуре методом стоячих волн. Экспериментально полученное значение скорости меньше теоретически рассчитанного значения в силу «не чистоты» опыта, а также в силу того, что молярная масса воздуха отлична от стандартного значения (содержатся примеси). |
,м/с
,м/с
,м/с
. Коэффициент Стьюдента для N = 30 (при доверительной вероятности P = 95%) равен 2,2, коэффициент 
