Задача 3. Определение удельного веса стандартной продукции
 Скачать 42.99 Kb. Скачать 42.99 Kb.
|
|
Задача 5.3. ПВ целях контроля за соблюдением норм расхода сырья проведено выборочное обследование партии готовой продукции. При механическом способе отбора 2 % изделий получены следующие данные о весе обследованных единиц:
При условии, что к стандартной продукции относятся изделия с весом от 2001 до 2100 г, установите для всей партии: 1) с вероятностью 0,95 возможны пределы удельного веса стандартной продукции (50%); 2) с вероятность 0,997 возможные пределы среднего веса одного изделия в генеральной совокупности (50%). Определение удельного веса стандартной продукции: Определение выборочной доли изделий, имеющих стандартный вес: W = m/n = 85/113 = 0,7522 m - число образцов в интервалах со стандартным весом n – общее число образцов Определение генеральной совокупности N = 113/ 0,02 = 5650 образцов (0.02 так как выборка 2%) Определение средней ошибки выборочной доли для бесповторного отбора  0,04021 шт. 0,04021 шт.Определение предельной ошибкивыборочной доли Определение доверительного интервала, т.е. генеральной доли образцов, имеющих стандартный вес: от 0,7522 - 0,07962 до 0,7522 + 0,07962 или от 0,693905 до 0,853265. Умножив полученные данные на 5300, получаем от 3564,674 до 44408,646 изделий. Определение средней ошибки выборочной средней для бесповторного отбора Расчет дисперсии
Определение выборочной средней (  = 233831,5 / 113 = 2069,3053 г; = 233831,5 / 113 = 2069,3053 г;  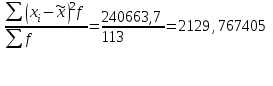 (г) (г)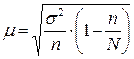 = =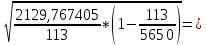 18,47055 г 18,47055 г . . 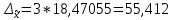 г гВывод: С вероятностью 99,7% можно утверждать, что средний уровень веса изделия в генеральной средней находится в пределаx: от от 2069,3053 –  до 2069,3053 + до 2069,3053 +  т.е. от 2013,893 до 2124,717 г. т.е. от 2013,893 до 2124,717 г. |

 )2fi
)2fi