Юбельт. Определитель минералов. Определитель минералов
 Скачать 1.68 Mb. Скачать 1.68 Mb.
|
|
Рис. 4. Упорядоченное атомное строение кристалла обусловливает различное расстояние между атомами в разных направлениях. Все доступные для измерения свойства кристаллов, такие, как характер прохождения света, теплопроводность, электропроводность и др., определяются анизотропией. Свободно висящей капле жидкости свойственна форма шара. Свободно выросший кристалл никогда не будет иметь такой формы. Он отграничен от своего окружения гранями, углами и ребрами. У многих кристаллов наблюдаются разные размеры в трех различных направлениях. Полиэдрический (многогранный) облик кристаллов, выросших из расплавов, растворов или паров, где отсутствуют пространственные ограничения, также является следствием анизотропии. Газы, жидкости или стекла не имеют кристаллического строения: они обладают одинаковыми свойствами во всех направлениях. Их называют изотропными веществами. А вот столь ценный «хрусталь» (свинцовое стекло), будучи стеклом, носит свое название не по праву [Слово «хрусталь» представляет собой искаженное слово «кристалл»; по-немецки оба слова звучат одинаково. — Прим. перса.]! Однако часто по внешнему облику кристаллов нельзя предположить, что их свойства различны в разных направлениях. Нередко кристаллы выглядят так, будто они состоят из зеркально-равных частей. При повороте кристаллов большинства минералов на определенный угол многократно наблюдается один и тот же облик кристаллов. Действительно, кристаллы обладают свойствами, ограничивающими их анизотропию. Существуют направления, вдоль которых проявляются одинаковые свойства. Такие кристаллы называются симметричными. Под симметрией в общем смысле понимается закономерное повторение какого-либо одного мотива. Это определение нарочито дано в такой общей форме, поскольку под термином «мотив» следует понимать все свойства и их взаимодействия в кристалле. Сюда относятся в обязательном порядке положение граней, углов и ребер у кристаллического многогранника, а также физические и химические свойства кристалла. Различают элементы симметрии нульмерные, одномерные и двумерные. Сочетание элементов симметрии лежит в основе принципа классификации кристаллов, выделения кристаллографических классов (видов) и кристаллографических сингоний. Нульмерным элементом симметрии является центр симметрии (символ Z, или 1); (читается: единица с минусом). Он обусловливает наличие у каждой грани кристалла параллельной ей противоположной грани, получаемой при помощи зеркального отражения этой грани в точке (операция называется инверсией). Одномерные элементы симметрии — это повторные оси (оси симметрии), которые приводят кристалл к совмещениям с самим собой путем вращения на определенный угол. Они носят обозначения 1, 2, 3, 4 и 6. Их углы вращения вычисляются путем деления 360° на 1, 2 и т. д. Так получаются углы 360, 180, 120, 90 и 60°. Тройная ось симметрии обусловливает, например, тот факт, что кристалл кварца, повернутый на 120°, снова демонстрирует тот же облик. Двумерным элементом симметрии является плоскость зеркального отражения, или плоскость симметрии (символ т), разделяющая кристалл на зеркально-равные части. Способы действия элементов симметрии и их распределение по отдельным кристаллографическим классам показаны в табл. 2. Показательно, что у многих минералов проявляется несколько аналогичных или разнородных элементов симметрии. Строгий вывод, который здесь опущен, доказывает, что всего существует 32 класса симметрии, отличающихся либо отдельными элементами симметрии, либо их допустимыми закономерными сочетаниями. Каждый минерал и каждый кристалл относятся лишь к одному из 32 классов симметрии. Таблица 2 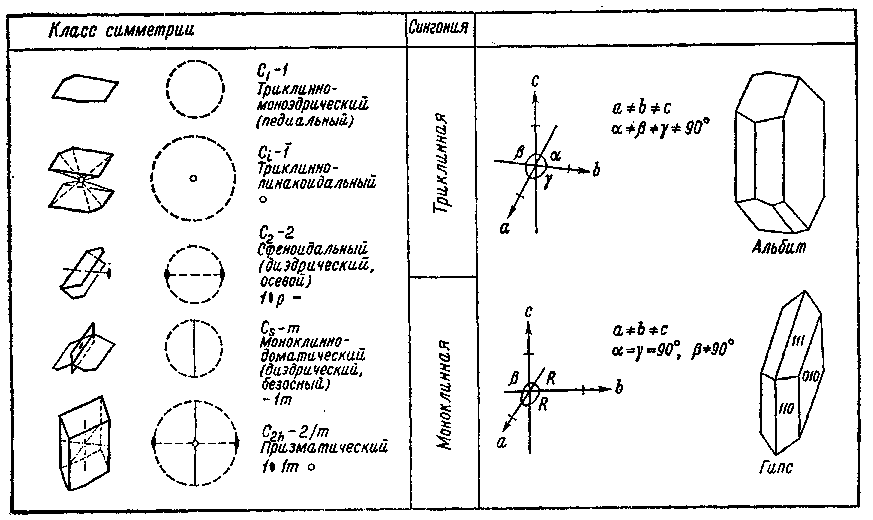 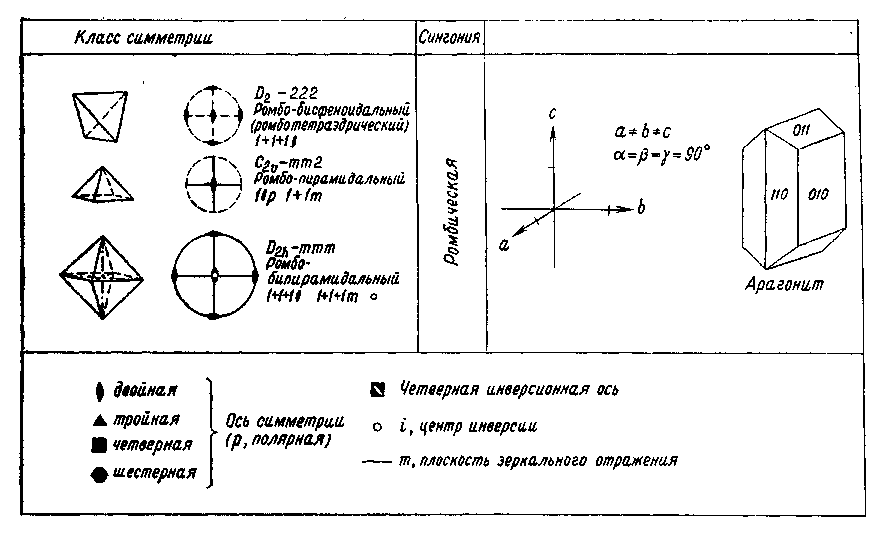 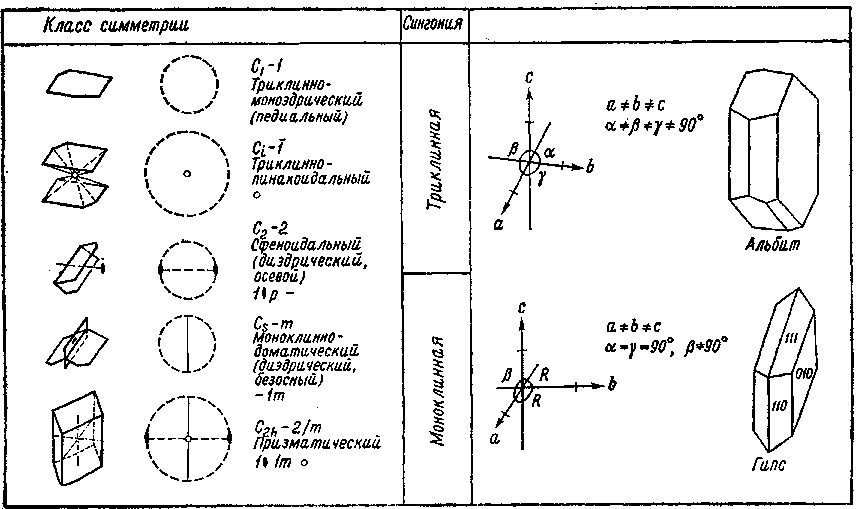 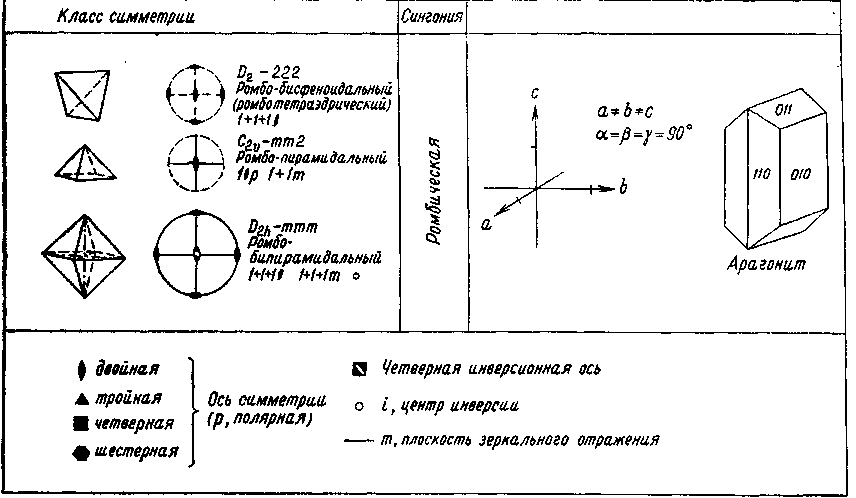 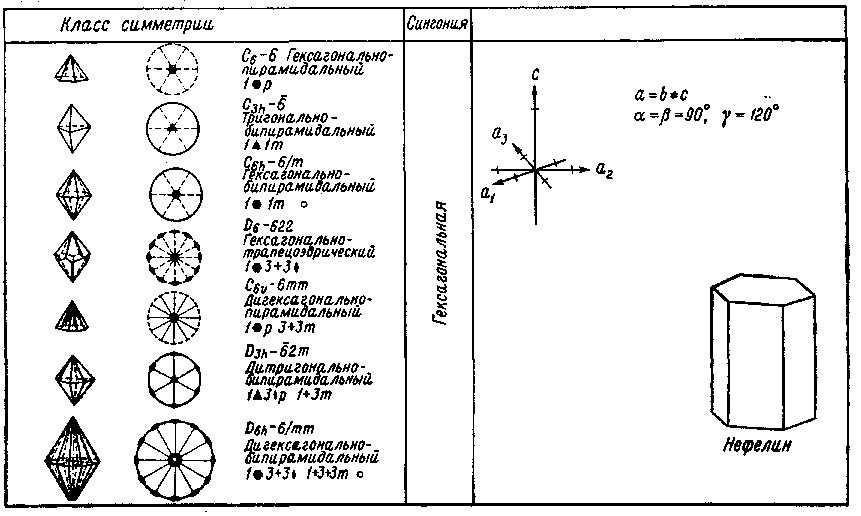 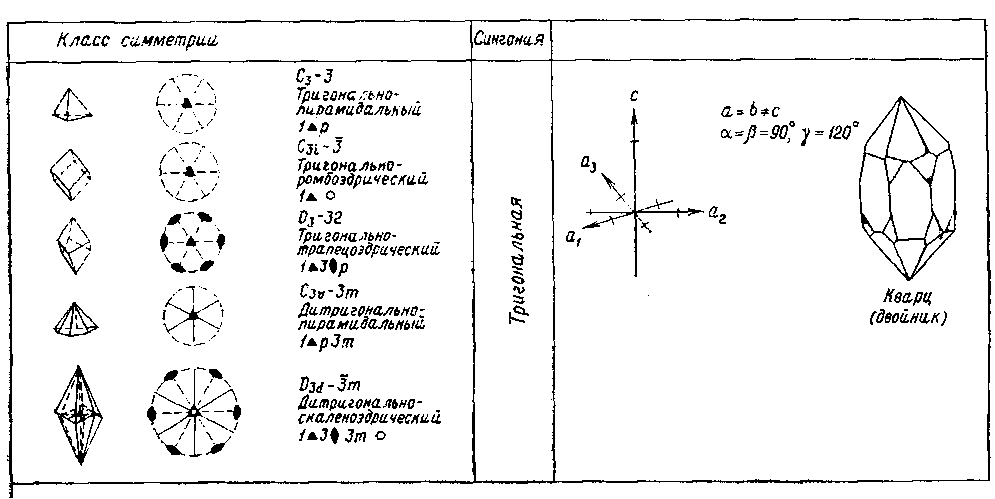 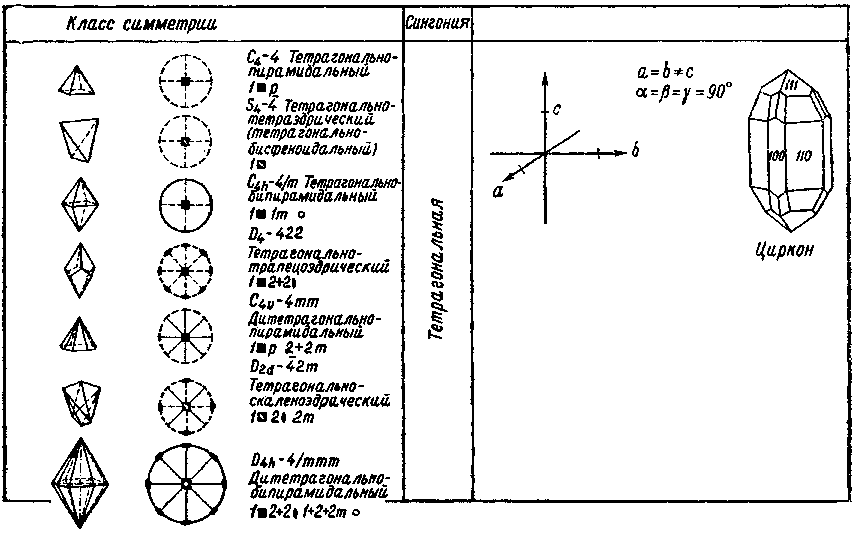 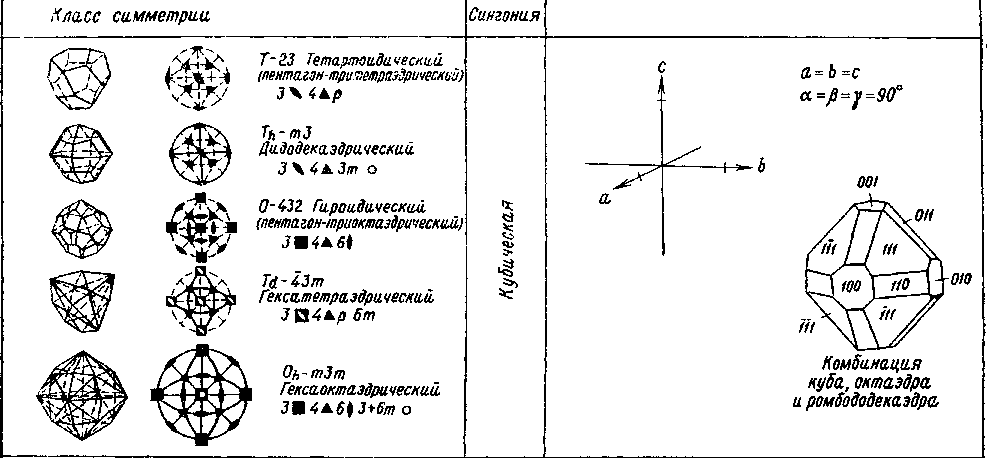 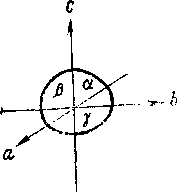 Рис. 5. Нижеследующее сопоставление иллюстрирует три ныне еще употребительные системы обозначений (символов) классов симметрии. Пример: С4h — 4/m — тетраго-нально-бипирамидальный. C4h — это символ по Шенфлису, 4/m — по Герману — Могену. Последнее обозначение исходит из обобщенной кристаллографической формы и ведет свое начало от Грота. Система обозначений по Герману — Могену (интернациональная символика) получает все более широкое распространение. 32 класса симметрии распределяются по шести кристаллографическим сингониям, которые вследствие своей малочисленности и более легкой распознаваемости являются, конечно, более наглядными. А сами сингонии выводятся из общих законов симметрии. Что понимают под сингонией? Она выводится из мысленно помещенной внутри кристалла системы координатных кристаллографических осей, причем соотношение длин отрезков по осям и величина углов между ними строго определенные для каждой сингонии. Установка системы кристаллографических осей всегда производится таким образом, что к наблюдателю обращена ось а, направо располагается ось b, а вверх направлена ось с. Между осями а и bзаключен угол у, между осями а и с— угол |3, а между осями b и с — угол а (рис. 5). Каждая сингония охватывает несколько классов симметрии (см. сопоставление в табл. 2). Сравнительный обзор показывает, что каждый класс легко подчинить соответствующей сингонии, поскольку каждая сингония характеризуется определенным набором элементов симметрии. В триклинной сингонии может присутствовать в качестве элемента симметрии только 1 — ось идентичности (вращение на 360°) или 1 как нульмерный элемент симметрии. В моноклинной сингонии существует три класса симметрии, характеризующиеся наличием двойной оси симметрии, плоскости симметрии или комбинацией обоих элементов. При сочетании трех двойных осей или плоскостей симметрии возникает ромбическая сингония. Четверная ось симметрии характеризует тетрагональную, шестерная — гексагональную и тройная — тригональную сингонию. Последняя рассматривается как подсистема гексагональной. Кубическая сингония определяется присутствием тройных осей симметрии, которые, однако, в отличие от тригональной сингонии во всех классах кубической сингонии в обозначениях ставятся на второе место. Примеры: 432 — кубическая, 422 — тетрагональная, или 23 — кубическая, 32 — тригональная. Следует, однако, показать яснее, что кристаллографические сингонии определяются непосредственно симметрией кристаллов. Наличие тетрагональной оси симметрии предопределяет условие а=b, угол между этими осями равен 90°. Ведь если вращение на 90° должно привести к идентичной картине, необходимо, чтобы отрезки по обеим осям были одинаковы. Аналогичные соотношения имеют место в гексагональной сингонии. В кубической сингонии соответственно три двойные или четверные оси симметрии связаны с четырьмя тройными осями, располагающимися вдоль пространственных диагоналей куба; обе системы осей пересекаются под характеристическим углом 54°44'. Следует поставить важный вопрос, обсуждение которого еще более прояснит соотношения между сингонией, классом симметрии и элементом симметрии. Расположены ли элементы симметрии в кристалле произвольно или и здесь выявляются закономерные соответствия? Оказывается, что элементы симметрии тесно связаны с кристаллографическими осями. Для отдельных сингонии установлены следующие главные направления (параллельные лучу зрения):
Главными направлениями в кристалле называются направления, в которых располагаются элементы симметрии. Отсюда следует, что элементы симметрии могут находиться только в строго определенных направлениях. В триклинной сингонии главное направление не установлено, поскольку придавать направление оси идентичности 1 или 1, т. е. точке, было бы бессмысленно. В моноклинной сингонии достаточно одного направления и для класса 2/m, поскольку эта комбинация оси и плоскости располагается в кристалле таким образом, что нормаль (перпендикуляр) к двойной оси ориентирована параллельно плоскости симметрии. Для других сингонии необходимо указывать три главных направления, хотя в кристаллах этих сингонии может присутствовать большое количество направлений, но два или даже три из них являются равноценными (например, в тетрагональной сингонии а=bили в кубической а = b = с), так что указание одного из таких направлений включает в себя и остальные, ему адекватные. Поскольку каждый класс симметрии подчиняется какой-либо одной сингонии, с помощью главных направлений определяется положение элементов симметрии в пространстве. Само собой разумеется, что существует и обратная связь, в соответствии с которой кристаллографическим осям отвечают определенные элементы симметрии. Примеры:
|| —параллельно _|_—перпендикулярно Пример класса 6 показывает, что не в каждом классе симметрии все главные направления соответствующей сиигонии сопровождаются элементами симметрии. Внешнюю огранку кристаллов составляют грани, ребра и углы, которые связаны между собой соотношением Эйлера: число граней+число углов=число ребер +2. Подобно элементам симметрии следует привести также грани и ребра кристаллов в соответствие с кристаллографическими осями и тем самым с элементами симметрии. Легко представить, что каждая грань, рассматриваемая в пространстве, заключенном в систему координатных осей, должна отсекать, пересекать одну, две или три оси. Различают ряд положений граней, представленных на рис. 6. Ребра кристаллов также обозначаются тройным индексом: ось а и все параллельные ей ребра имеют индекс [100], ось b— [010] и ось с— [001]. Общий символ грани, пересекающей все три оси,— (hkl), ребра— [uvw]. Обратите внимание на различную форму скобок! Необходимо упомянуть еще одну особенность. Если грань отсекает на оси а одну часть, на оси b — две части и располагается параллельно оси с, то ее индекс будет не (120), а (210). Для индицирования граней, согласно Миллеру, применяются обратные значения для длин отрезков по осям. Грань отсекает отрезки a, b и с в отношении 1 : 2 : оо. Обратные значения составляют 1/1 : 1/2:1/оо, а приведенные к целым числам— (210). 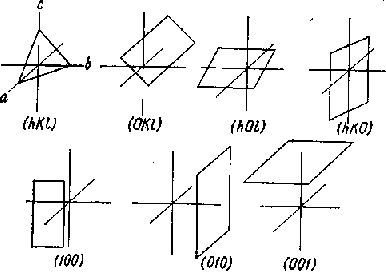 Рис. 6. Рис. 6. 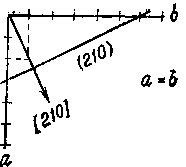 Рис. 7. Рис. 7.Для индицирования ребер, наоборот, используется прямое отношение отрезков. Благодаря применению обратных и прямых отрезков достигается одинаковое написание индексов для некоторых граней и нормалей к ним (рис. 7). Для грани в общем положении принимается индекс (hkl), а для соответствующих ребер— [uvw]. Какие числа скрываются за этими буквенными обозначениями? Это малые числа (целые), часто 1 и 0, реже 2. Числа больше 2 почти не появляются в обозначениях индексов праней и ребер. Тот факт, что длины отрезков, отсекаемых гранями или ребрами на трех основных осях [Отрезки, отсекаемые гранью по кристаллографическим осям, в отечественной литературе принято называть параметрами этой грани.— Прим. перев.], относятся между собой как малые целые рациональные числа, носит название в кристаллографии закона рациональности отношений параметров. Необходимо подчеркнуть, что абсолютные значения величин, между которыми определяют отношения, не во всех случаях одинаковы. Для ромбической сингонии а=/=b=/=с. Это означает для грани (111) ромбического кристалла различные абсолютные значения отрезка, отсекаемого по каждой оси, но равное количество этих отрезков по а, Ь и с. Так что получается отношение 1а:1b:1с. По равенству или неравенству величин или длин отрезков по a, b и с определяют кристаллографические сингонии. Прямое отношение а : b : с, упрощенно а : 1 : с, обозначается как геометрическое осевое отношение. В кубической сингонии оно составляет, естественно, 1 : 1 : 1, в тетрагональной и гексагональной 1 : 1 : с, а начиная с ромбической и в сингониях с более низкой симметрией — а: 1 : с. Осевое отношение является константой вещества. Если мы знаем это отношение и установили, что оно равно таковому известного минерала, тогда с полной уверенностью можно говорить об идентичности обои : минералов. 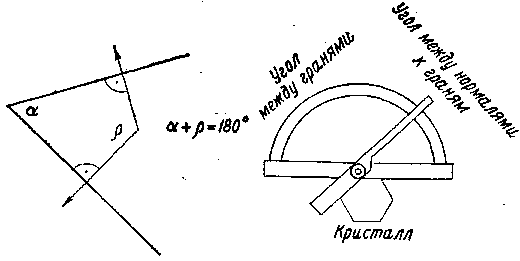 Рис. 8. В заключение следует познакомить любителей минералов с методом, который позволяет во многих случаях более точно диагностировать минералы, но о котором, однако, в большинстве определителей минералов не упоминается. В описаниях минералов в данной книге наряду с сингонией приведены также класс симметрии и геометрическое осевое отношение, что облегчает возможность сравнения. Если минералы встречаются в искаженных формах, то сингония и тем более класс симметрии определяются лишь с трудом. Но искажение не затрагивает углов между кристаллографическими гранями. Углы между одинаковыми гранями кристалл-всегда одинаковы. Установлением этого закона постоянства углов Стеной в 1669 г. заложил основы кристалле графин. Углы между кристаллографическими гранями измеряются гониометром. Следует различать гранные углы и углы между нормалями к граням. Первые дополняют вторые до 180°. С помощью простого прикладного гониометра, который легко изготовить из транспортира и полоски картона, при аккуратной работе могут быть измерены углы с точностью до ±1°. Соответствующие грани минерала крепко зажимают между транспортиром и картонной линейкой (рис. 8) и считывают значение угла между нормалями и гранями. Необходимо учитывать, что последующие вычисления действительны только для углов между нормалями к граням. 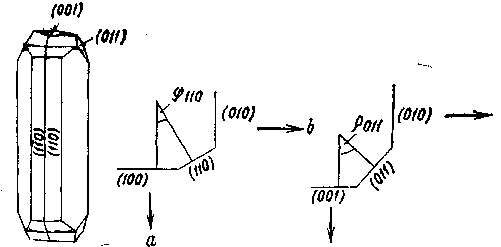 Рис. 9. Что вообще подлежит вычислению? Не что иное, как геометрический индекс минерала — его осевое отношение а: 1 : с. Согласно закону рациональности отношений параметров, у кристалла следует ожидать наличия граней с малыми индексами. Углы между нормалями к граням (110) и (100) и (011) и (001) дают возможность очень просто вычислить осевое отношение. Поскольку отношение а: b : с может быть выражено как а : 1 : с, его можно записать также в виде а/b и с/b, тем самым придав вычислению большую наглядность. В ромбическом кристалле, например в топазе, измерению подлежат следующие углы. Принимая во внимание только кристаллографические оси и линию их пересечения со следом граней (НО) и (011), мы получаем треугольники с углами ф и р (рис. 9). Отношение а/b задается тангенсом ф, а отношение с/b — тангенсом р (рис. 10). 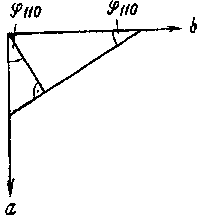 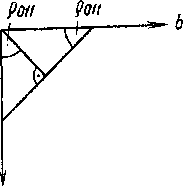 |
