Математика. Математика_Ощепков Д.Э.. Ощепков Данил Эдуардович

• Название: Ощепков Данил Эдуардович
• Анкор: Математика
• Дата: 22.11.2020
• Размер: 191 Kb.
• Имя файла: Математика_Ощепков Д.Э..doc
• Тип: Документы; #152646

Частное профессиональное образовательное учреждение «ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ КОЛЛЕДЖ»

Практическое задание

по	математике

дисциплине

Выполнил(а) студент(ка)	Ощепков Данил Эдуардович
			фамилия имя отчество
Идентификационный номер:		2001-0800

Пермь 2020

Задание №1.

Вычислить предел при

а) x₀ = 1;

б) x₀ = 2;

в) x₀ = ∞.

Решение.

а) .

Прямая подстановка предельного значения позволяет найти предел:

.
б) .

Подстановка предельного значения даёт неопределённость:

.

Чтобы избавиться от неопределённости вида (0/0), разложим числитель и знаменатель на множители, а затем сократим общий множитель (x – 2):


в) .

Подстановка предельного значения даёт неопределённость:

.

Чтобы избавиться от неопределённости вида (∞/∞), разделим числитель и знаменатель на аргумент в наивысшей степени, присутствующей в дроби, то есть, на :

.

Ответ:_а)'>Ответ: а) ; б) ; в) .

Задание №2.

Найти производные функций:

а) y = 2x² – 2/√x + sin(п/4);

б) y = cosx / (1 + sinx);

в) y = 2^x cosx;

г) y = ln√x³ + 4.

Решение.

а) .

Используем правила дифференцирования.

Производная суммы (разности) функций равна сумме (разности) производных:

.

Постоянный множитель можно вынести за знак производной:

.

Используя производную от степенной функции, получим:

.

Ответ: .
б) .

По правилу дифференцирования частного двух функций имеем:

.

Далее, используя правила дифференцирования и таблицу производных, получаем:



Ответ: .
в) .

Используя правило дифференцирования произведения двух функций и таблицу производных, получаем:



Ответ: .

г) .

Используя правило дифференцирование сложной функции и таблицу производных, получим:



Ответ: .


Задание №3.

Исследовать данную функцию методами дифференциального исчисления и построить её график.

y = 4x / (16 + x²).

Решение.

1) Поскольку при любом , то область определения функции:

.
2) Функция непрерывна на всей области определения.
3) Чётность-нечётность.

.

Так как , то функция нечётная (график функции симметричен относительно начала координат).
4) Найдём первую производную функции:

;

при .


− + −




Экстремумы:

− максимум функции;

– минимум функции (в силу нечётности функции).

Интервалы монотонности:

– функция убывает;

– функция возрастает.
5) Найдём вторую производную функции:



;

при .


− + − +




Точки перегиба:

;

;

(в силу нечётности функции).

Интервалы выпуклости и вогнутости:

– график функции выпуклый;

– график функции вогнутый.
6) Асимптоты графика функции.

Вертикальные асимптоты.

Поскольку функция определена на всей числовой прямой, то вертикальных асимптот нет.

Горизонтальные асимптоты.

;

– в силу нечётности функции.

– горизонтальная асимптота.

Наклонных асимптот нет.
7) График функции пересекает координатные оси в точке .
Строим график функции 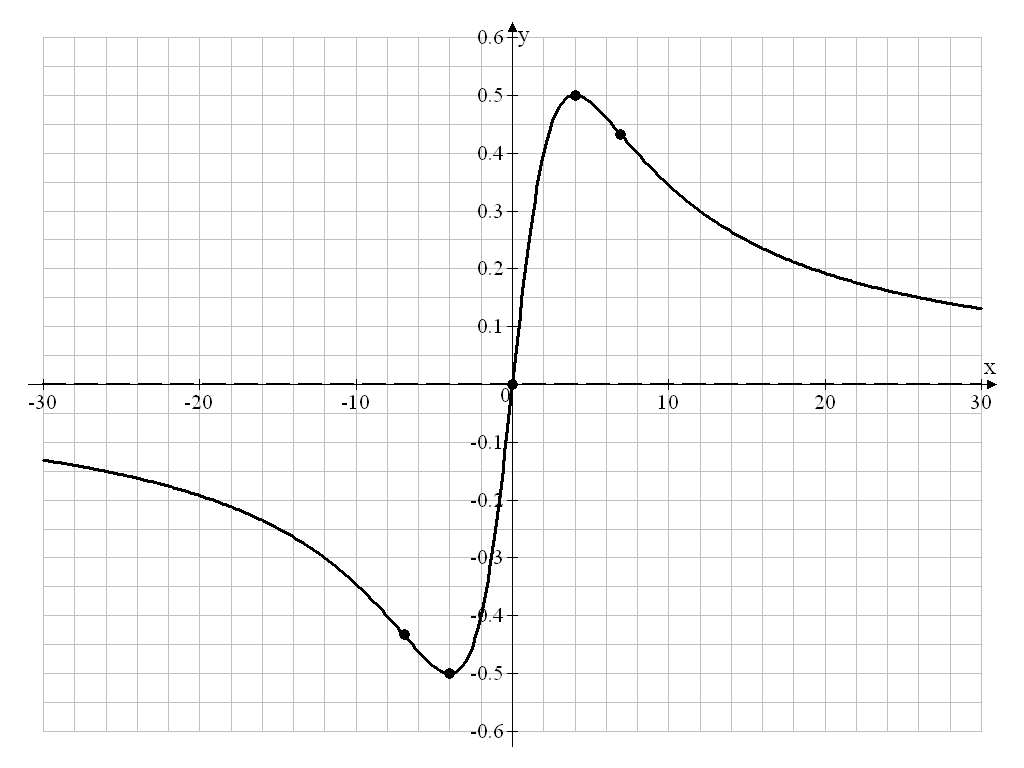по результатам проведённого исследования.














Задание №4.

Вычислить неопределённые интегралы:

а) ;

б) ;

в) .

Решение.

а) .

Используем метод интегрирования по частям:



Выполним проверку:



. (верно)

Ответ: .
б) .

Используем метод замены переменной. Положим: . Тогда:

;



Возвращаясь к исходной переменной , окончательно получаем:

.

Ответ: .
в) .

Используем метод замены переменной. Положим: . Тогда:

;

.

Возвращаясь к исходной переменной , окончательно получаем:

.

Ответ: .

Задание №5.

Вычислить площадь фигуры, ограниченной линиями y = x² – 4x + 3 и y = x – 1. Построить график.

Решение.

Находим точки пересечения параболы и прямой:

;

; .

Находим точки пересечения параболы с осью Ox:

.

Определяем координаты вершины P параболы:

.

Строим линии (прямую проводим через точки A и B; параболу – через точки A, B, C, P) и выделяем фигуру, которую они образуют.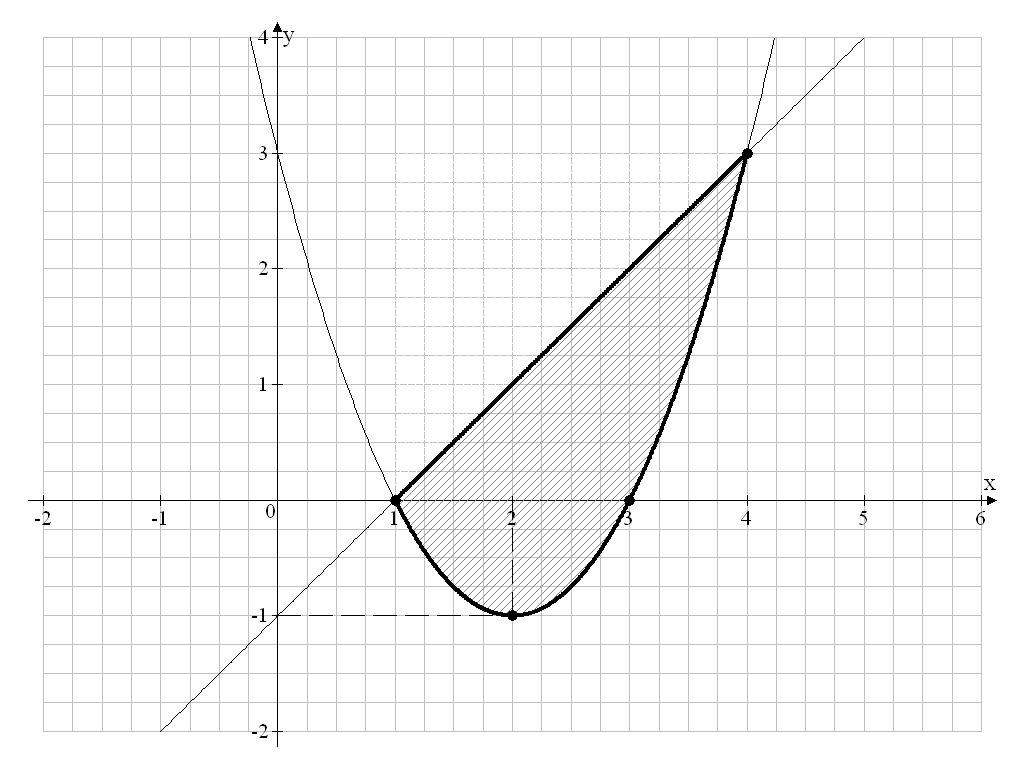



B


y₁ = x – 1

A C


y₂ = x² – 4x + 3
P


Вычисляем площадь фигуры:



Ответ: ед².