Зачет логика Лупандин. Ощущение элементарный чувственный образ, отображающий отдельные, единичные свойства предмета. Можно изолированно ощущать вкус, цвет, запах, звук и т д. Например, для лимона характерны ощущения кислоты, желтизны и т д. Восприятие

• Название: Ощущение элементарный чувственный образ, отображающий отдельные, единичные свойства предмета. Можно изолированно ощущать вкус, цвет, запах, звук и т д. Например, для лимона характерны ощущения кислоты, желтизны и т д. Восприятие
• Анкор: Зачет логика Лупандин.docx
• Дата: 22.01.2018
• Размер: 173.53 Kb.
• Имя файла: Зачет логика Лупандин.docx
• Тип: Документы; #14776

1. Чувственное и рациональное познание

Познание – процесс накопления, переработки, хранения и передачи информации об окружающем мире. Принято различать 2 ступени познания: чувственное и рациональное (мышление). Именно мышление является объектом изучения логики, а его формы и законы – предметом.

Чувственное познание опирается на образы, возникающие в сознании.

К формам чувственного познания относят:

Ощущение - элементарный чувственный образ, отображающий отдельные, единичные свойства предмета. Можно изолированно ощущать вкус, цвет, запах, звук и т.д. Например, для лимона характерны ощущения кислоты, желтизны и т.д.;

Восприятие - отображение не отдельных свойств, а их системы, целостности. Например, мы воспринимаем лимон не как кислоту или желтизну, а как целостный предмет. Наше восприятие лимона включает в себя и его цвет, и его вкус, и его запах в неразрывном единстве: оно подразумевает не работу отдельного чувства, а согласованную деятельность нескольких или всех основных чувств;

Представление - чувственный образ предмета, который возникает в сознании в отсутствие этого предмета. Например, если мы когда-либо видели лимон, мы вполне можем представить его себе, даже если он не находится перед нами и не может воздействовать на наши органы чувств. В представлении большую роль играют память, воспоминания, а также воображение человека. Представление можно назвать восприятием предмета в его отсутствие. Возможность представления и его близость к восприятию обусловлены тем фактом, что чувственные образы возникают не в органах чувств, а в коре головного мозга. Поэтому непосредственное присутствие предмета не является необходимым условием для возникновения чувственного образа.

Рациональное познание, основанное на абстрактном мышлении, позволяет человеку выйти за ограниченные рамки чувств.

К формам рационального познания относят:

Понятие — мысль, которая отражает предметы, явления и связи между ними в обобщенной форме. Например, понятие «человек» не тождественно простому чувственному образу какого-то конкретного человека, а обозначает в обобщенном виде мысль о любом человеке — кем бы он ни был. Аналогично понятие «стол» включает в себя образы всех столов — различной формы, размеров, окраски, а не какой-либо определенный образ стола. Таким образом, понятие схватывает не отдельные признаки предмета, а его сущность, в частности, в случае стола — его функции, использование (перевернутый ящик тоже может входить в понятие «стол», если он используется в таком качестве);

Суждение - это отрицание или утверждение чего-либо при помощи понятий. В суждении между двумя понятиями устанавливается связь. Например, «Золото есть металл»;

Умозаключение — рассуждение, в ходе которого из одних суждений — посылок выводится другое, заключительное суждение — вывод.
2. Общая характеристика понятий

Понятие – форма мышления с помощью которой человек обозначает объекты, раскрывая их смысл. Под объектом принято понимать материальные предметы, явления, события, процессы. Понятие раскрывает смысл объекта на основе его существенных признаков.

Существенными называются признаки, каждый из которых необходим, а вместе они достаточны для того, чтобы раскрыть смысл объекта. Признаки не позволяющие сделать это – несущественные и в состав понятия не входят.

Каждое понятие формируется на основе существенных признаков с помощью следующих действий: анализ, синтез, абстрагирование, сравнение, обобщение, индукция, дедукция.

В языковой форме понятие выражается словом или словосочитанием.
3. Содержание и объем понятия. Виды понятий по объему.

В процессе формулировки «понятие» в него закладываются 2 взаимосвязанные характеристики: содержание понятия и объем понятия.

Содержание – это совокупность существенных признаков предметов, на основании которых они выделяются и обобщаются.

Объем понятия – это предмет или совокупность предметов, обладающих признаками, составляющими содержание понятия.

Содержание и объем взаимосвязаны между собой по следующим закономерностям:

• 
  Содержание понятий определяет его объем
  
• 
  Чем больше содержание понятие, тем меньше его объем.
  

Виды понятий по объему

В зависимости от объема различают 3 группы понятий:

• 
  Общие – объем которых составляет 2 и более элемента
  
• 
  Единичные – объем составляет 1 элемент
  
• 
  Нулевые – объем не имеет ниодного элемента.
  

4. Содержание и объем понятия. Виды понятий по содержанию.

В зависимости от содержания принято различать 4 группы понятий:

• 
  конкретные и абстрактные. Конкретными называются понятия, в которых мыслятся предметы в совокупности своих признаков («стол », « стул », «человек», « дерево »). Абстрактными называются понятия, в которых мыслятся свойства или отношения, отвлеченные от самих предметов («счастье», « белизна», «бесконечность»).
  
• 
  соотносительные и безотносительные. Соотносительные – такие понятия, в которых выражаются предметы, существование одного из которых немыслимо без существования другого («дети » и « родители », « начальник» и « подчиненный», «верх », «низ»). Безотносительные – такие понятия, в которых отражаются предметы, существование которых не связывается необходимым образом с существованием других предметов («человек», «книга», «парта»).
  
• 
  положительные и отрицательные. Положительными называются понятия, которые выражают наличие у предмета определенных признаков («красивый», « доблесть », « возможность »). Отрицательными называются такие понятия, в которых выражается отсутствие признака, зафиксированного в положительном понятии (« некрасивый», «невозможность », «нехороший »). Отрицательные понятия образуются от положительных посред -ством прибавления к положительным понятиям отрицательной частицы « не », приставки « без». Если без отрицательной частицы понятие не употребляется, то оно является положительным (например, «неряха », «ненастье »).
  
• 
  Собирательные и несобирательные. Собирательные – понятия, обозначающие группу объектов как единое целое. Несобирательные – обозначают каждый объект в отдельности.
  

5. Отношения между совместными понятиями.

Совместные – понятия, объемы которых совпадают полностью или частично. Для таких понятий характерны отношения: тождество, пересечение, подчинение.

Тождественными считаются понятия, объемы которых полностью совпадают. Например:
А: Самое глубокое озеро в мире – Байкал



В: Озеро Байкал.
Пересекающимися называются понятия, объемы которых совпадают частично. Например:

А: Студент

В: Спортсмен

Подчинение. Одно из понятий, обладающее большим объемом, включает в себя понятие с меньшим объемом. Например:

А: Фрукт



В: Яблоко
6. Отношения между несовместными понятиями.

Несовместные – понятия, объемы которых полностью исключают друг друга. Для таких понятий характерны отношения: соподчинение, противоречие, противоположности.

Соподчинение. Понятия, объемы которых полностью исключают друг друга, но при этом они одновременно подчиняются другому, более общему понятию.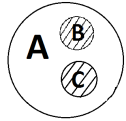



А: Фрукт

В: Яблоко

С: Груша
Противоречие. Понятия, объемы которых полностью исключают друг друга, при этом одно из утверждает признаки объекта, а другое их отрицает: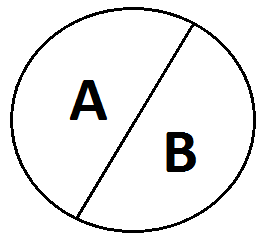



А: Человек, имеющий экономическое образование.

В: Человек, не имеющий экономического образования.
Противоположности. Понятия, объемы которых исключают друг друга, но при этом одно из понятий утверждает признаки объекта, а другое не только их отрицает, но и выдвигает свои новые признаки: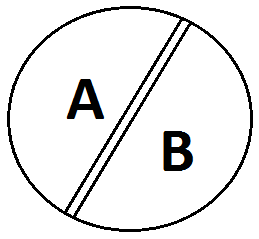



А: Человек, имеющий экономическое образование.

В: Человек, имеющий юридическое образование.
7. Логическая операция «обобщение и ограничение понятий»

Ограничение понятий – это логическая операция, посредством которой совершается переход от понятия с большим объемом к понятию с меньшим объемом. Например: населенный пункт  город  столица  столица РФ. При этом каждое последующее понятие должно подчиняться каждому предыдущему.

Обобщение понятий – это логическая операция, посредством которой совершается переход от понятия с меньшим объемом к понятию с большим объемом. Например: населенный пункт  город  столица  столица РФ.
8. Логическая операция «определение понятий». Правила явного определения.

Определение понятий – логическая операция , раскрывающая содержание понятия, т.е. выясняется смысл объекта действительности. В составе этой логической операции принято различать 2 вида понятий: Определяемое понятие (Dfd) с помощью которого устанавливается смысл объекта, т.е. содержание, которое необходимо раскрыть. Определяющее понятие (Dfn) с помощью которого раскрывается содержание определяемого понятия.

Правила определения:

• 
  Определение должно быть соразмерным. Правило соразмерности требует, чтобы объем определяемого понятия был равен объему определяющего: Dfd=Dfn. Нарушение этого правила ведет к двоякого рода ошибке: 1) слишком широкое определение, когда объем определяющего понятия шире объема определяемого понятия. 2) слишком узкое определение, когда объем определяющего понятия меньше объема определяемого.
  
• 
  Определяемое понятие не должно быть зацикленным
  
• 
  Определение должно быть ясным, не допускающим двусмысленности, т. е. должно быть сформулировано в однозначно определенных терминах.
  
• 
  Определение не должно содержать художественно-образных средств и оценок.
  
• 
  Нельзя определять понятия через такие термины , которые сами нуждаются в определениях.
  
• 
  Определение по возможности не должно быть отрицательным.
  

9. Логическая операция «Деление понятий». Правила деления.

Деление понятий – логическая операция , посредством которой раскрывается объем понятия, т.е. выясняется из каких элементов понятие состоит.

В составе данной логической операции различают следующие структурные части:

Исходное понятие (делимое) – понятие, объем которого необходимо раскрыть.

Основание деления (делитель) – признак по которому делится исходное понятие.

Элементы деления (результат деления) – итоговые понятия на которые делится исходное.

Правила деления:

• 
  Объем исходного понятия должен быть равен сумме объемов элементов деления. Если это правило не соблюдается, возникают 2 ошибки: 1) Неполное деление когда перечисляются не все возможные элементы деления. 2) Чрезмерное деление когда выделяются лишние элементы деления, не подходящие под исходное основание деления.
  
• 
  Деление должно производиться по одному основанию
  
• 
  Члены деления должны исключать друг друга, т. е. находиться в отношении несовместимости
  
• 
  Деление должно происходить последовательно без переходов на другой уровень деления.
  

10. Общая характеристика суждений.

Суждение – форма мышления, посредством которой что-либо утверждается или отрицается о предмете и которая обладает логическим значением истины или ложности.

По своей структуре суждение представляет собой взаимосвязанные понятия и включают в свой состав элементы:

Субъект – понятие, обозначающее тот объект, о котором в суждении ведется речь.

Предикат – понятие, обозначающее признак объекта о котором ведется речь.

Логическая связка – осуществляет взаимосвязь между субъектом и предикатом простого суждения, а также, между простыми суждениями в составе сложных. Логическая связка в одних случаях может выражаться: (являться, есть, может быть). В других случаях может выражаться с помощью символов: (–). В третьих – может просто подрузамеваться.

Квантарное слово – количественная характеристика того объекта, о котором ведется речь.

Квантары делятся: общие (все, каждый, всякий, любой). Частные (некоторые, этот).

Каждое суждение может принимать 2 значения: истинное суждение содержит информацию которая соответствует окружающей действительности. Ложное если такого соответствия нет.

Истинность простого суждения зависит только от содержащейся в нем информации, а истинность сложного определяется не только его информацией, но и его структурой.

В языковой форме суждения выражаются с помощью предложений.

11. Виды простых суждений (суждения существования, свойства, отношений).

Простые суждения – суждения, в составе которых взаимосвязан только один субъект и один предикат.

По назначению простые суждения делятся на:

Суждения существования, в которых утверждается или отрицается существование самих объектов действительности. Характерная черта таких суждений – наличие в их составе таких слов, как: бывают, встречаются, существуют, есть.

Суждения свойств, в которых утверждаются или отрицаются определенные свойства объектов.

Суждения отношений, в которых утверждаются или отрицаются определенные отношения между объектами. Характерная черта – наличие следующих параметров: пространства, времени, величины, родства.
12. Объеденная классификация простых суждений по количеству и качеству.

В зависимости от качества делятся на: утверждающие и отрицающие. В зависимости от количества делятся на: общие и частные. Для того, что бы представить полную логическую характеристику простых суждений, эти параметры объединяются:

Общеутвердительные (класс А)

Все S есть P

Общеотрицательные (класс Е)

Все S не есть P; Ни одно S не есть P

Частноутвердительные (класс I)

Некоторые S есть Р; Это S есть Р

Частноотрицательные (класс О)

Некоторые S не есть Р; Это S не есть Р
13. Распределенность логических терминов в простых категорических суждениях.

Распределенность терминов – это количественная характеристика субъекта и предиката в суждении.

Термин считается распределенным, если его объем либо полностью включен в объем другого термина, либо полностью из него исключен. Или иначе – термин считается распределенным, если он мыслится в полном объеме. Для распределенного термина характерно кванторное слово « все», для нераспределенного – «некоторые».

Термин считается нераспределенным, если его объем совпадает частично с объемом другого термина.

Графически распределенность терминов изображается с помощью круговых схем и штриховки той части терминов, которые мыслятся в суждении.
14. Отношения между совместимыми простыми суждениями по правилам «логического квадрата».

Простые суждения могут быть сравнимыми и не сравнимыми.

Сравнимые – простые суждения, которые имеют одинаковые по смыслу субъект и предикат.

Несравнимые – простые суждения, которые различаются либо по субъекту, либо по предикату, либо по тому и другому одновременно.

Сравнимые делятся на совместимые и не совместимые.

Совместимые простые суждения могут быть одновременно истинными, несовместимые одновременно истинными быть не могут. Для совместимого простого суждения характерны отношения: тождество, частичного совпадения и подчинения.

Тождественными считаются сравнимые простые суждения, имеющие одинаковую логическую связку и одинаковое квантарное слово. Для таких суждений характерно следующие условие: если одно из них истинно, то другое должно быть истинным. Если одно из таких суждений ложное, то другое должно быть ложным.

Частично совпадающие – сравнимые простые суждения, которые имеют одинаковое квантарное слово, но разную логическую связку. Для частного совпадения характерно следующие условие: если одно из суждений истинно, то другое может быть истинным или ложным. Если одно из суждений ложное, то другое только истинно.

В подчинение вступают простые сравнимые суждения, которые имеют одинаковую логическую связку, но разное квантарное слово. Если общее суждение истинно, от подчиняющееся ему частное будет истинно. Если общее ложно, то подчиняющееся частное ложно или истинно.
15. Отношения между несовместимыми простыми суждениями по правилам «логического квадрата».

Для несовместных характерны отношения: противоположности и противоречия.

Противоположные - простые суждения, которые имеют одинаковое по количеству общее слово, но различную логическую связку. Если одно из таких суждений истинно, то другое ложно. Если одно ложное, то другое и ложное и истинное.

Противоречивые – простые суждения, которые имеют различное квантарное слово и разную логическую связку.
16. Коньюктивные сложные суждения и условия их истинности.

Конъюнктивное суждение – суждение, которое является истинным тогда и только тогда, когда истинны все входящие в него суждения. Образуется посредством логического союза конъюнкции, выражающегося грамматическими союзами « и », « да », « но», «однако».

a	b	a ∧ b
И	И	И
И	Л	Л
Л	И	Л
Л	Л	Л

17. Дизъюнктивные сложные суждения и условия их истинности.

Имеется два вида дизъюнктивных суждений: строгая ( исклю -чающая) дизъюнкция и нестрогая ( неисключающая) дизъюнкция.

Строгая (исключающая) дизъюнкция – сложное суждение, принимающее логическое значение истины тогда и только тогда, когда истинно только одно из входящих в него суждений. Например, «Данное число либо кратно, либо не кратно пяти».

a	b	a ∨ b
И	И	Л
И	Л	И
Л	И	И
Л	Л	Л

Нестрогая (неисключающая) дизъюнкция – сложное суждение, принимающее логическое значение истины тогда и только тогда, когда истинным является , по крайней мере, одно из простых суждений, входящих в сложное. Нестрогая дизъюнкция выражается посредством грамматического союза « или …или »

a	b	a ∨ b
И	И	И
И	Л	И
Л	И	И
Л	Л	Л

18.Импликативные сложные суждения и условия их истинности.

Импликация – сложное суждение, принимающее логическое значение ложности тогда и только тогда, когда предшествующее суждение истинно, а последующее ложно . В естественном языке импликация выражается союзом « если ..., то »

a	b	a → b
И	И	И
И	Л	Л
Л	И	И
Л	Л	И

19 Эквивалентные сложные суждения и условия их истинности.

Эквивалентность – сложное суждение, которое принимает логическое значение истины тогда и только тогда, когда входящие в него суждения обладают одинаковым логически значением , т. е . одновременно либо истинны , либо ложны . Логический союз эквивалентности выражается грамматическими союзами « тогда и только тогда, когда», «если и только если ».

a	b	a ↔ b
И	И	И
И	Л	Л
Л	И	Л
Л	Л	И

20. Деление простых и сложных суждений по модальности.

Всякое суждение может быть рассмотрено с точки зрения модальности ( лат. м odus – мера, способ , вид ). Модальность – характеристика суждения в зависимости от степени устанавливаемой им достоверности, т. е . от того , утверждается ли в нём возможность, действительность или необходимость чего-либо.

В традиционной формальной логике суждения по модальности делятся на три группы: суждения возможности, суждения действительности и суждения необходимости .

В суждении возможности отражается вероятность наличия или отсутствия признаков у предмета – напр.: « Возможно, в этом году я поеду к морю».

В суждении действительности констатируется наличие или отсутствие у предмета того или иного признака – напр.: « Некоторые числа делятся на 5».

В суждении необходимости отображается такой признак, который является необходимым , существенным для предмета – напр.: «Живые организмы не могут существовать без обмена веществ ».

Модальность – одно из важнейших свойств суждения, так как она выражает степень существенности того или иного признака для данного предмета, отображённого в суждении.
21. Основные логические законы: закон тождества.

Закон тождества фиксирует одно из коренных свойств мышления – его определенность . Согласно этому закону всякая мысль в процессе рассуждения должна быть тождественна самой себе. Это означает, что предмет мысли должен рассматриваться в одном и том же содержании своих признаков на всем протяжении рассуждения или доказательства .

Из существа этого закона вытекает важное требование: нельзя нетождественные мысли принимать за тождественные, нельзя различные мысли принимать за тождественные . Мысль должна быть сформулирована таким образом, чтобы не допускалась многозначность используемых терминов.

Нарушение требования, вытекающего из закона тождества, ведет к логической ошибке – «подмене понятия». Сущность ее состоит в том, что вместо данного понятия употребляется другое. Отождествление понятий чаще всего происходит неосознанно, в силу многозначности языка, однако иногда подмена производится пред -намеренно, сознательно.
22. Основные логические законы: закон непротиворечия.

Закон непротиворечия выражает требование непротиворечивости и последовательности мышления. Это значит, что, признав известные положения в качестве истинных и развивая выводы из этих положений, мы не можем допустить в своем рассуждении или доказательстве никаких утверждений, противоречащих тому, что было сказано ранее.

Закон непротиворечия гласит : два находящихся в отношении отрицания суждения не могут быть одновременно истинными; по крайней мере одно из них необходимо ложно. Следует иметь в виду, что данный закон действителен лишь в отношении тех суждений, в которых говорится об одном и том же предмете , взятом в одно и то же время и в одном и том же отношении . В случаях, где данное условие не выполняется, закон противоречия неприменим.
23. Основные логические законы: закон исключенного третьего.

Согласно этому закону, из двух противоречащих высказываний одно и только одно истинно. Это тот случай, когда « третьего не дано », т. е. истинное высказывание не может заключаться между противоречащими высказываниями.

Подобно закону противоречия закон исключенного третьего выражает последовательность и непротиворечивость мышления. Он требует ясных определенных ответов, указывая на невозможность отвечать на один и тот же вопрос в одном и том же смысле и « да » и « нет», на невозможность искать нечто среднее между утверждением чего -либо и отрицанием того же самого.
24. Основные логические законы: закон достаточного основания.

Выражает требование доказательности, обоснованности мысли . Согласно этому закону , всякая истинная мысль должна быть обоснована другими мыслями , истинность которых уже доказана . Мысли ( суждения), которые приводятся для обоснования истинности других мыслей, называются логическим основанием. Мысль, которая вытекает из других как из основания, называется логическим следствием.

Фиксируя внимание на требовании указания аргументов ( оснований ), обладающих достаточной силой доказательности, этот закон помогает отделить истину от ложности и тем самым прийти к верным выводам. Чрезвычайно большое значение закон достаточного основания имеет в юридической практике.
25. Общая характеристика умозаключений.

Умозаключение – форма мышления с помощью которой человек на основе исходной информации, при соблюдении определенных правил, строит вывод об объекте действительности.

Каждое умозаключение представляет собой совокупность взаимосвязанных суждений и включает в свой состав следующие элементы:

Посылка (предпосылка) – суждение, которое содержит исходную информацию об объекте. С посылок начинается построение вывода, а их число может изменяться от 1 до бесконечности.

Заключение (вывод) – суждение, содержащее итоговую информацию об объекте. Процесс построения вывода завершается заключением, само заключение может быть только одно.

Логическая связка разграничивает посылки и заключения между собой и показывает переход от посылок к выводу. Связка может быть выражена словами: следовательно, значит, поэтому, в итоге, таким образом, итак.

Умозаключение может быть истинным или ложным. Считается истинным, если его вывод соответствует действительности. Ложным, если такого соответствия нет. В языковой форме каждое умозаключение выражается взаимосвязанными предложениями.

26. Простой категорический силлогизм: сущность и структура.

Простой категорический силлогизм – дедуктивное умозаключение, которое сроится на основе 2 посылок, представляющие собой простые суждения. В состав посылок входят 3 вида терминов:

Средний – понятие, которое находится в составе обоих посылок, осуществляет между ними взаимосвязь, но в выводе не отражается. Обозначается (М).

Больший – понятие, которое входит в состав только первой посылки, а в выводе – предикат (Р).

Меньший – понятие, содержащиеся в составе второй посылки, а в выводе – субъект (S).
27. Фигура и модус силлогизма.

Для проверки вывода простого силлогизма на истинность, используют 2 взаимосвязанных параметра: фигура, модус.

Фигура представляет собой схему. Которая показывает различное расположение среднего термина в посылках. Различают 4 типа фигур:

Фигура 1-го типа Фигура 2-го типа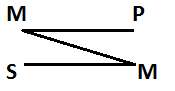


Фигура 3-го типа Фигура 4-го типа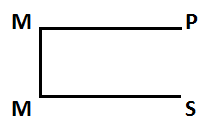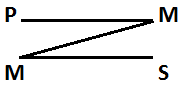


Модус – схематическое изображение классов простых суждений, входящих в состав силлогизма. Различают 19 правильных модусов, которые подтверждают истинность вывода простого силлогизма. При этом для 1 фигуры характерны 4 правильных модуса, для 2 тоже 4, для 3 – 6. Для 4 – 5.

1 фигура: 2 фигура: 3 фигура: 4 фигура:

AAA AEE AAI AEE

AII AOO AII IAI

EAE EAE IAI AAI

EIO EIO OAO EAO

EAO EIO

EIO
28. Правила построения простого категорического силлогизма.

Правила делятся на две группы: правила терминов и правила посылок.

Правила терминов

1. В простом категорическом силлогизме должно быть три термина. Нарушение этого правила ведет к ошибке – « учетверение термина ». Она происходит из -за нарушения закона тождества, когда один и тот же термин используется в разных смыслах . Например:

Движение – вечно

Хождение в университет – движение

Хождение в университет – вечно.

2. Средний термин должен быть распределен хотя бы в одной из посылок. Нарушение этого правила демонстрирует следующий пример: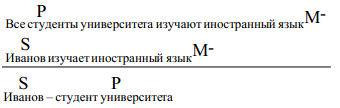



Средний термин – «изучают иностранный язык» занимает место предиката в утвердительных суждениях, следовательно, нераспределен ни в одной из посылок, так как предикаты распределены в отрицательных суждениях. Заключение в данном силлогизме лишь вероятностное.

3. Термин, не распределенный в посылках, не может быть рас-пределен и в заключении. Нарушение этого правила делает заключе -ние лишь вероятностным . Например:



Больший термин – « человек» в большей посылке не распределен, так как занимает место предиката утвердительного суждения. В заключении он распределен, так как занимает место предиката отрицательного суждения.

Правила посылок

1. Из двух отрицательных посылок заключение не следует с необходимостью. Следовательно, одна из посылок должна быть утвердительной. Нарушение этого правила можно продемонстрировать на примере:



2. Из двух частных посылок заключение не следует с необходимостью. Например:



3. Если одна из посылок отрицательная, то и заключение должно быть отрицательным.



4. Если одна из посылок – частное суждение, то и заключение должно быть частным:


29. Условные дедуктивные умозаключения.

Условные дедуктивные умозаключения - это умозаключения, посылками и заключением которого являются условные суждения. Например:


30. Разделительные дедуктивные умозаключения.

Разделительные дедуктивные умозаключения (разделительные силлогизмы) состоят из посылок являющихся разделительными (дезинъюнктивными) суждениями.


31. Условно-разделительные умозаключения.

Условно-разделительный силлогизм – умозаключение, в котором одна посылка является условным суждением, а другая – разделительным .

В зависимости от того, сколько следствий установлено в условной посылке, различают дилеммы, трилеммы, n – леммы.

Лемма – означает по-гречески предложение. В выводе такого умозаключения утверждается альтернатива, т.е. необходимость выбора только одного из всех возможных предложений. Таким образом, дилемма – это условно-разделительное умозаключение с двумя альтернативами. Различают следующие виды дилемм: простые и сложные, конструктивные и деструктивные.

Простая конструктивная дилемма («рассуждение по случаю»)



Сложная конструктивная дилемма отличается от простой тем, что оба следствия из условной посылки различны.



Простая деструктивная дилемма. В условной посылке этого умозаключения из одного и того же основания вытекают два различных следствия; вторая посылка представляет собой дизъюнкцию отрицания обоих следствий; в заключении отрицается основание.



Сложная деструктивная дилемма содержит одну посылку, состоящую из двух условных суждений с разными основаниями и разными следствиями; вторая посылка есть дизъюнкция отрицаний обоих следствий; заключение является дизъюнкцией отрицаний обоих оснований.



32. Индуктивное умозаключение. Его структура и виды.

Индуктивное умозаключение – умозаключение, при построении которого происходит переход от более частной информации к более общей. Особенностью индукции является то, что в отличие от дедуктивных умозаключений, она позволяет строить вероятностный вывод. Если в дедуктивных умозаключениях истинность вывода определяется правилами их построения, то в индуктивных истинность вывода определяется фактической ситуацией. Поэтому вывод индукции в одних случаях может быть истинным, а в других – ложным.

Структура индуктивных умозаключений включает в себя посылки 2 различных типов, вывод – логическую связку между ними.

В посылках 1-го типа говорится о принадлежности определенного признака конкретному объекту действительности. В посылках 2-го типа говорится о принадлежности самих объектов к определенной однородной группе (классу объектов). В соответствии с этим в выводе индукции говорится о принадлежности ранее изучаемого признака всей однородной группе объекта.

В зависимости от кол-ва изучаемых объектов индукция может быть полной и не полной. Индукция считается полной, если в процессе ее построения изучаются все без исключения объекты, входящие в состав однородной группы. Используется в тех случаях, когда число изучаемых объектов не велико или у человека имеется возможность, время изучить все объекты в отдельности. Индукция считается неполной, если в процессе ее построения исследуется только часть объектов, входящих в состав однородной группы. Результат изучения этой части, в последствии, переносится на всю группу. Используется в случаях, когда число объектов велико, либо когда нет времени.
33. Методы построения неполной индукции.

Метод сходства основан на следующем правиле: если два и более случаев наблюдаемого явления сходны только в одном обстоятельстве , то это одно обстоятельство, вероятно, и есть причина данного явления.

Метод различия основан на сравнении двух или более случаев, когда исследуемое явление наступает и когда оно не наступает. Подобные случаи должны быть сходны во всем, за исключением одного обстоятельства. Обстоятельство, в котором разнятся сравниваемые случаи, и есть причина или же часть причины исследуемого явления.

Таким образом, если случай, в котором данное явление наступает, и случай, в котором оно не наступает, сходны во всем за исключением одного обстоятельства, то это единственное обстоятельство является причиной исследуемого явления. Заключение, полученное по методу различия, обладает большей степенью вероятности, чем заключение, полученное по методу сходства.

Метод сопутствующих изменений. Если какое-либо явление изменяется определенным образом всякий раз, когда изменяется предшествующее ему явление, то эти явления, вероятно, находятся в причинной связи друг с другом.

Метод остатков. Если известно, что причиной исследуемого явления не служат необходимые для него обстоятельства, кроме одного, то это обстоятельство будет, вероятно, причиной данного явления.
34. Умозаключение по аналогии: его структура и виды.

Аналогичными называются умозаключения, при построении которых вывод о сходстве объектов в одних признаках строится на основе их сходства в других признаках. При построении умозаключения по аналогии происходит переход, либо от частной информации к частной. Либо от общей к общей. Поскольку вывод в умозаключениях по аналогии, так же как и в индукции, подтверждается фактическими обстоятельствами, он имеет вероятностный характер.

В зависимости от того, по каким признакам сравниваются объекты, аналогия может быть строгой, дающий достоверный вывод и не строгой, дающий вероятностный вывод.

В строгой аналогии объекты сравниваются только по существенным признакам. В не строгой объекты могут сравниваться как по существенным, так и по не существенным признакам.