|
Учитель. Трехфазные цепи (1). Основа электроэнергетики. С тех пор, как гениальный россиянин Александр Осипович ДоливоДобровольский
https://yandex.ru/video/preview/?filmId=4233582190622722962&from=tabbar&parent-reqid=1606211868503555-1780745379253447743100163-production-app-host-man-web-yp-224&text=%D0%B2%D0%BC%D0%B4%D0%B5%D0%BB%D0%BB%D0%B5%D0%BA%D1%86%D0%B8%D1%8F+%D1%82%D1%80%D0%B5%D1%85%D1%84%D0%B0%D0%B7%D0%BD%D1%8B%D0%B5+%D1%86%D0%B5%D0%BF%D0%B8
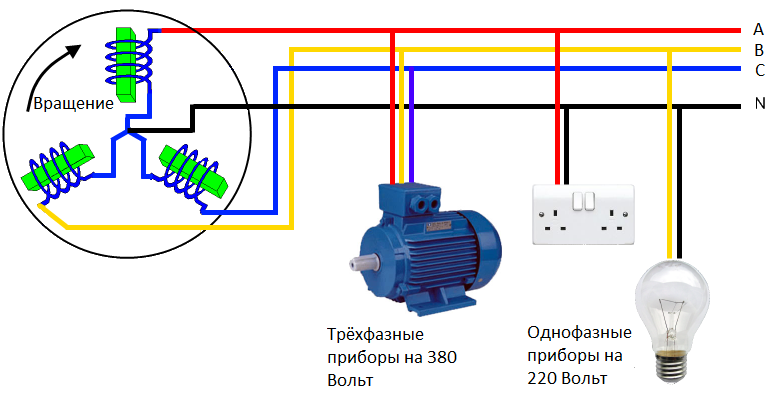
Схема работы трёхфазной сети
Три фазы это основа электроэнергетики. С тех пор, как гениальный россиянин Александр Осипович Доливо-Добровольский внедрил эту инновацию в массовое применение, весь мир был опоясан миллионами километров электрических проводов и десятками миллионов электродвигателей, которые объединяет одно - они все работают на трёхфазном напряжении.
Не думаю, что будет преувеличением сказать: знать, как работает система на трёх фазах это необходимое условие для каждого, кто интересуется технологиями и имеет инженерную "жилку".
Почему именно три фазы?
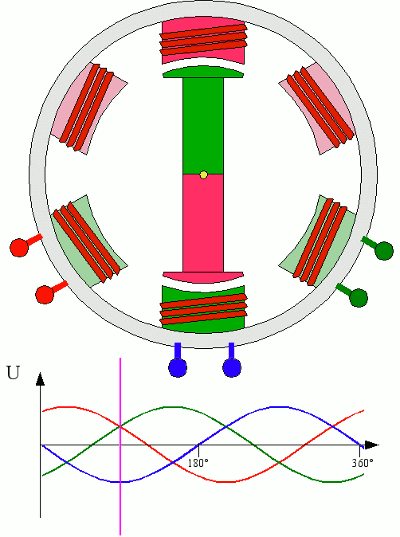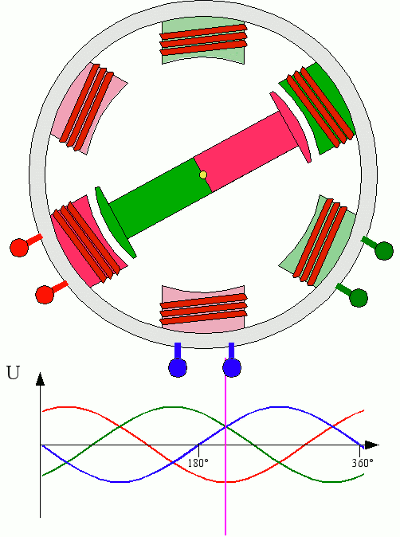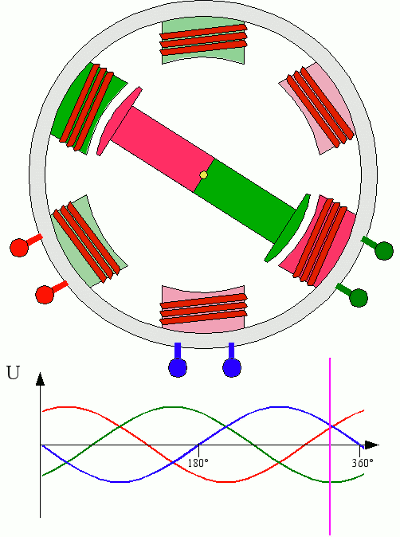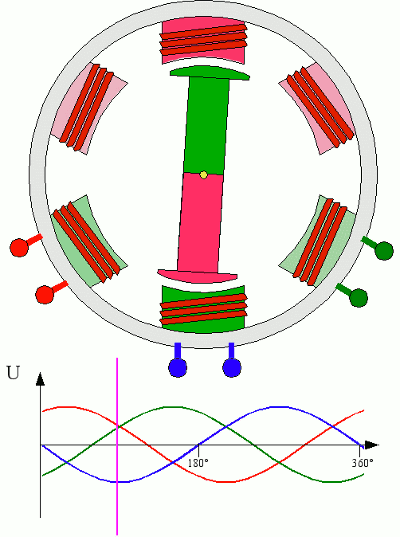
Принцип действия трёхфазного электродвигателя
Три фазы - это минимальное число полюсов, которое способно надёжно запускать, с помощью вращающегося магнитного поля, ротор электродвигателя. Большее число полюсов ведёт к усложнению конструкции двигателя (и трансформаторов) и ничего не даёт взамен. На этом "прокололся" разрекламированный Никола Тесла: вместо того, чтобы сосредоточиться на трёх фазах, он пытался внедрить многофазные системы, что, в итоге, определило его провал.
Даже само число "три" намекает на некую гармонию, завершённость. Стулу нужно минимум три ножки, чтобы стоять не падать, пирамида - самая надёжная конструкция, созданная человеком, имеет боковую стенку в виде треугольника и так далее.
Как это работает?
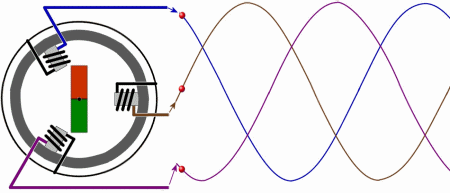
Напряжение на каждой и фаз в разные моменты времени
Если мы подключим к каждому проводу трёхфазного источника тока осциллограф - прибор, рисующий колебания напряжения на временной шкале, мы увидим, что на каждом из них ток имеет идентичную форму - синусоиды. Но каждая из них будет сдвинута относительно соседней на 120 градусов, то есть на 1/3 периода.
Например, в тот момент, когда на фазе А напряжение равно нулю, на фазе В напряжение, пройдя максимум, снижается, а фаза С, где полярность тока уже сменилась имеет отрицательный (обратно направленный ток).
Через треть периода (0,007 сек) "на нуле" будет уже фаза С, фаза А пройдёт пик, снижаясь к нулю, а фаза В (как С, треть периода назад) будет иметь обратную полярность. И так по кругу.
380 и 220 Вольт - "инь и янь" бытового электричества
Если мы подключим, в любой момент времени, между любыми двумя проводами вольтметр переменного тока, он покажет одну и ту же цифру - 380 Вольт. Это так называемое "линейное напряжение". Откуда же в наших розетках берётся значение напряжения 220 Вольт? Здесь "вступает в игру" четвёртый провод - нейтраль или "ноль".
Строго говоря, для передачи энергии и работы трёхфазных приборов, ноль не требуется. Ток (благодаря сдвигу синусоид) прекрасно перетекает от фазы к фазе, выполняя любую нужную работу - вращение двигателя, нагрев ТЭНа или освещение, если найти светильник на 380 Вольт. Ноль нужен в двух случаях:
когда нужно запитать однофазный прибор;
если нужно, для целей защиты людей, обеспечить заземление.
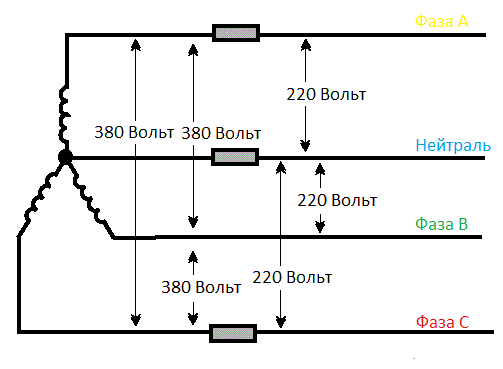
Трёхфазная система с нейтралью
Однофазные приборы намного проще в устройстве, а следовательно - дешевле. Выгоды очевидны, да и заземление штука нужная, когда электричеством пользуются люди, далёкие от основ электробезопасности. А делается ноль очень просто. Все три фазы соединяются одним "хвостом" вместе. Между оставшимися концами напруга по-прежнему 380 Вольт. А вот между "свободным" хвостом и точкой соединения уже меньше (в 1,73 раза) - 220 Вольт ("фазное напряжение"). К этим выводам можно подключать ваш утюг, компьютер и светильник, имеющие по два провода питания - они будут работать как надо.
Простота и гениальность системы трёх фаз - в её универсальности. К одной и той же линии могут быть подключены простые приборы на 220 Вольт и мощные электродвигатели на трёх фазах, маломощные настольные лампы и сверхмощные плавильные печи и всё будет работать без перебоев и долгие годы. Главное, чтобы хватило мощности источника тока - генератора или трансформатора.
И, как "вишенка на тортик" - при передаче энергии на большие расстояния, трёхпроводная линия, по сравнению с двухпроводной, обходится на треть дешевле, благодаря экономии на проводах.
Расчет трехфазных цепей переменного тока https://study.urfu.ru/Aid/Publication/6210/1/Электротехника.%20Трехфазные%20электрические%20цепи.pdf
Трехфазные цепи переменного тока Википедия
https://ru.wikipedia.org/wiki/Трёхфазная_система_электроснабжения
Лекция . Принцип получения 3-фазной ЭДС. Основные схемы соединения 3-фазных цепей. Соединение 3-фазной цепи «звездой». Соотношение между фазными и линейными напряжениями и токами при симметричной нагрузке в 3-фазной цепи, соединённой «звездой». Назначение нулевого провода в 4-проводной цепи. Соединение нагрузки «треугольником». Активная, реактивная и полная мощности в 3-фазной цепи. Коэффициент мощности.
Трёхфазный генератор вырабатывает три синусоидальные э.д.с. одинаковой частоты и амплитуды, сдвинутые по фазе на 120о . Они образуют трёхфазную симметричную систему.
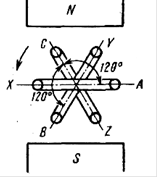 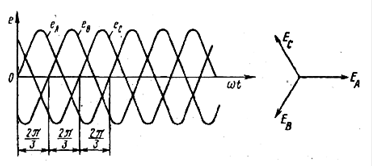
а) б) в)
Рис. а) Принципиальная схема трёхфазного генератора; б) Временная диаграмма вырабатываемой генератором э.д.с.; в) векторная диаграмма э.д.с.
Э.д.с. обмотки В отстаёт от э.д.с. обмотки А на 120о, а э.д.с. обмотки С опережает обмотку А на 120о.
еА = Em sin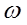 t ; eВ = Em sin ( t ; eВ = Em sin (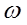 t - 120о) ; eС = Em sin ( t - 120о) ; eС = Em sin (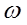 t + 120о) t + 120о)
Трёхфазные системы получили широкое применение так как :
- при одинаковых условиях питание трёхфазным током позволяет получить значительную экономию материала проводов по сравнению с тремя однофазными,
- при прочих равных условиях трёхфазный генератор дешевле, легче и экономичнее, чем три однофазных генератора такой же мощности,
- трёхфазная система токов позволяет получить вращающееся магнитное поле с помощью трёх неподвижных катушек. Это сильно упрощает производство и эксплуатацию трёхфазных двигателей.
Трёхфазный генератор, соединённый с трёхфазным потребителем проводами, образует трёхфазную цепь
1-й способ. НЕСВЯЗАННАЯ ТРЁХФАЗНАЯ ЦЕПЬ.
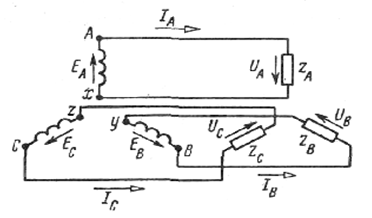
Рис. Принципиальная схема несвязанной трёхфазной цепи.
Каждая обмотка генератора питает свою фазную нагрузку. В практике практически не применяется.
2-способ. СОЕДИНЕНИЕ ТРЁХФАЗНОЙ ЦЕПМ ПО СХЕМЕ «ЗВЕЗДА»
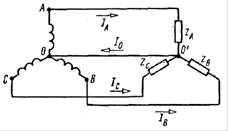 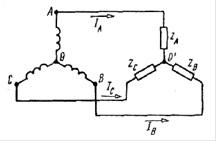 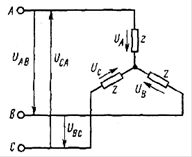
а) б) в)
Рис. а) Четырёхпроводная схема цепи по схеме «звезда»; б) трёхпроводная схема цепи по схеме «звезда»; в) параметры цепи по схеме «звезда».
Концы обмоток генератора соединены в одну точку О(N). Она называется НУЛЕВАЯ. Таким же способом соединена нагрузка с полными сопротивлениями ZА, ZВ, ZС с нулевой точкой O' (n).
Провод между точками О - O' называется нулевой или нейтральный. Четырёхпроводная схема.
Начала обмоток обозначаются буквами А,В,С.
Напряжения UАВ, UВС, UСА называются линейное напряжение Uл.
Напряжения UА, UВ, UС называются фазное напряжение Uф.
Токи IА, IВ, IС называются линейные токи Iл.
Токи I ZА, I ZВ, I ZС называются фазные токи Iф.
Ток I0 называется нулевой или нейтральный ток.
В четырёхпроводной системе по первому закону Кирхгофа I0 = IА + IВ + IС в векторной форме.
Основные соотношения между линейными и фазными токами и напряжениями:
Iл = Iф , то есть IА = I ZА , IВ = I ZВ , IС = I ZС, Uл = 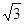 Uф , Uф ,
UАВ = UА – UВ UВС = UВ – UС UСА = UС - UА
При симметричной нагрузке, когда ZА= ZВ= ZС токи будут IА= IВ= IС при этом IА + IВ + IС=0
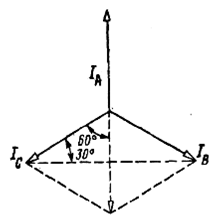 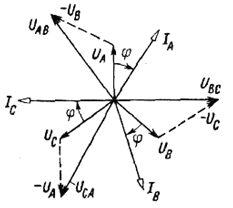 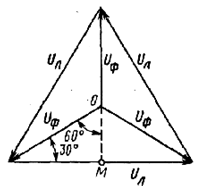
а) б) в)
Рис. а) Сложение векторов токов при симметричной нагрузке, б) векторная диаграмма при симметричной нагрузке, в) топографическая диаграмма напряжений при симметричной нагрузке.
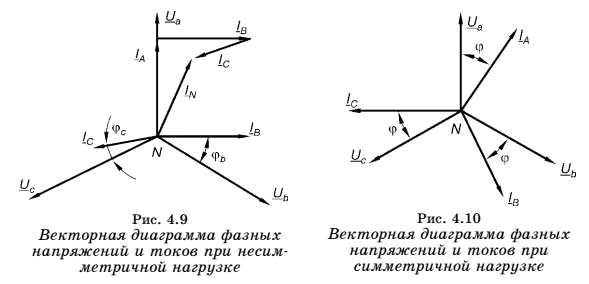
На векторной диаграмме изображены векторы токов, отстающих на угол 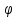 от векторов ,соответствующих фазных напряжений ( нагрузку считаем индуктивной). от векторов ,соответствующих фазных напряжений ( нагрузку считаем индуктивной).
Ток в нулевом проводе равен нулю при строго симметричной нагрузке. Если нагрузка
несимметричная, ZА 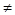 ZВ ZВ 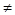 ZС . То неравными будут токи IА ZС . То неравными будут токи IА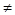 IВ IВ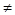 IС. При этом ток в нулевом проводе I0 IС. При этом ток в нулевом проводе I0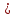 0, а фазные напряжения остаются неизменными. 0, а фазные напряжения остаются неизменными.
Нулевой провод в четырёхпроводной трёхфазной цепи необходим для обеспечения симметрии фазных напряжений при несимметричной нагрузке.
3– способ. СОЕДИНЕНИЕ ТРЁХФАЗНОЙ ЦЕПМ ПО СХЕМЕ «ТРЕУГОЛЬНИК».
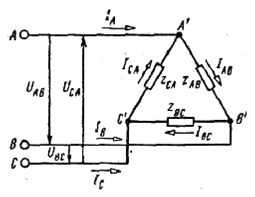 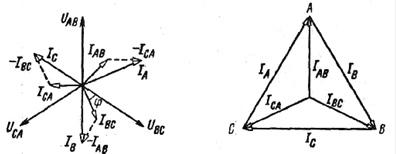
а) б) в)
Рис. а) Цепь по схеме «звезда», б) векторная диаграмма напряжений, в) векторная диаграмма токов при схеме «треугольник»
Фазные напряжения равны линейному.
Uл = Uф то есть UАВ = UВС = UСА =UZАВ = UZВС = UZСА
Iл =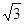 Iф , IА = IАВ – IСА , IВ = IВС – IАВ , IС = IСА – IВС смотри рис. в) Iф , IА = IАВ – IСА , IВ = IВС – IАВ , IС = IСА – IВС смотри рис. в)
При симметричной нагрузке IАВ = IВС = IСА так как ZАВ = ZВС = ZСА смотри рис. б)
При несимметричной нагрузке величина фазных токов IАВ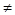 IВС IВС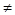 IСА и угол IСА и угол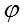 другой для фаз. другой для фаз.
АКТИВНАЯ, РЕАКТИВНАЯ И ПОЛНАЯ МОЩНОСТИ В ТРЁХФАЗНОЙ ЦЕПИ.
Активная мощность трехфазной цепи равна сумме активных мощностей ее фаз:
Р = РА + РВ + РС при этом Р = 3 Uф Iф соs 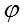
Реактивная мощность трехфазной цепи равна сумме реактивных мощностей ее фаз:
Q = QА + QВ + QС при этом Q = 3 Uф Iф sin 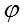
При симметрчной нагрузке Р = 3 Рф , Q = 3 Qф
Для каждой фазы можно определить: Р = I2 ф *R ф , Q = I2 ф *Х ф
При соединении по схеме «ЗВЕЗДА» Uл = 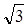 Uф и Iл = Iф тогда Uф и Iл = Iф тогда
Р = 3 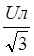 Iл соs Iл соs 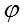 = = 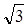 Uл Iл соs Uл Iл соs 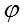 , Q = , Q =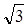 Uл Iл sin Uл Iл sin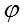 , ,
При соединении по схеме «ТРЕУГОЛЬНИК» Uл = Uф и Iл = 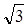 Iф тогда Iф тогда
Р = 3 Uл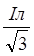 соs соs 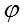 = = 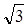 Uл Iл соs Uл Iл соs 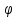 , Q = , Q =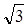 Uл Iл sin Uл Iл sin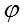 , ,
Полная мощность S = 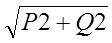
В каждой фазе соs 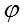 = = 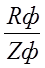
Чем больше различие фаз тем больше ток в нейтральном проводе.
При выборе схемы соединения нагрузки(звезда, треугольник, звезда с нулевым проводом)
необходимо учитывать три основных фактора: характер нагрузки, номинальное напряжение сети, номинальное напряжение потребителей. Рассмотрим примеры, иллюстрирующие выбор схем.
1. Определить схему соединения осветительной нагрузки, если Uсети=380В, Uлампы=220В.
Прежде всего устанавливаем, что лампы должны быть включены на фазное напряжение.
Действительно, 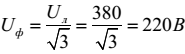 Поэтому выбираем схему соединения звездой. Поскольку нагрузка осветительная, нужно для обеспечения симметрии фазных напряжений включить нулевой провод. Следовательно, заданным условиям удовлетворяет схема соединения«звезда с нулевым проводом». Поэтому выбираем схему соединения звездой. Поскольку нагрузка осветительная, нужно для обеспечения симметрии фазных напряжений включить нулевой провод. Следовательно, заданным условиям удовлетворяет схема соединения«звезда с нулевым проводом».
2. Определить схему соединения осветительной нагрузки, если Uсети=220В, Uлампы=220В.
В рассматриваемом случае лампы должны быть включены непосредственно на линейное
напряжение. Выбираем схему соединения треугольником. Симметрия линейных напряжений обеспечивается генераторами, питающими сеть.
3. Выбрать схему соединения обмоток(фаз) трех фазного двигателя, если Uобм=220В,
Uсети=380В.
Обмотки трехфазного двигателя образуют симметричную нагрузку; следовательно, в
нулевом проводе нет необходимости. Если обмотки двигателя соединить треугольником, то каждая из них окажется под линейным напряжением 380В и будет перегреваться. Таким образом, обмотки двигателя следует соединить звездой. Тогда к каждой обмотке будет приложено напряжение, на которое она рассчитана: Uф=220В.
Пример решения задачи на расчет трехфазной цепи соединенной звездой.
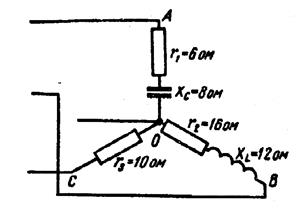
Puc. 6.
Задача: В каждую фазу трехфазной четырехпроводной сети включили сопротивления так, как показано на рис. 6. Величины сопротивлений даны на рисунке. Линейное напряжение сети U=380B. Определить: линейные токи, углы сдвига фаз, ток в нулевом проводе, активную, реактивную и полную мощности трех фаз. Построить в масштабе векторную диаграмму.
Решение. 1. Полные сопротивления фаз:
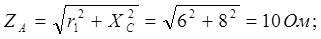 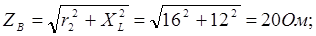
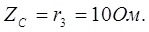
2. Углы сдвига фаз:
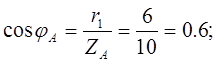 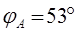 (опережающий); (опережающий);
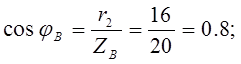 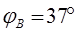 (отстающий); (отстающий);
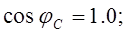 . .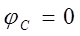
3. Фазное напряжение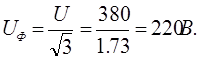
4. Линейные (фазные) токи:
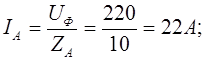
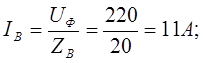
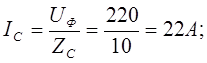
5. Активная мощность потребляется только активными сопротивлениями. Поэтому активная мощность трех фаз
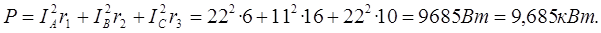
6. Реактивная мощность потребляется только реактивными сопротивлениями. Поэтому реактивная мощность трех фаз
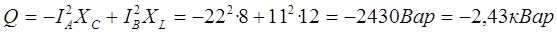
Знак «минус» показывает, что реактивная мощность системы носит емкостный характер.
7. Полная мощность трех фаз:
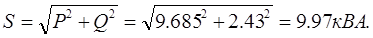
8. Построение векторной диаграммы начинаем с векторов фазных напряжений.
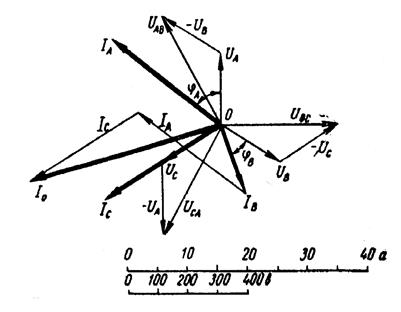
Рис. 7.
Из точки О (рис. 7) в принятом масштабе напряжений проводим три вектора фазных напряжений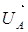 , , 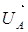 и и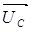 , углы между которыми составляют 120°. Затем строим векторы линейных напряжений , углы между которыми составляют 120°. Затем строим векторы линейных напряжений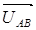 , , 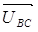 и и , согласно уравнениям: , согласно уравнениям:
 = = - - = = +(- +(- ); );
 = = - - = = +(- +(- ); );
 = = - - = = +(- +(- ) )
Черточки над буквами показывают, что векторы должны вычитаться и складываться геометрически. Например, для построения линейного напряжения  к вектору к вектору  нужно геометрически прибавить обратный по направлению вектор нужно геометрически прибавить обратный по направлению вектор  . .
Под углом φА=53° в сторону опережения вектора фазного напряжения  откладываем в принятом масштабе токов вектор тока откладываем в принятом масштабе токов вектор тока  ; под углом φВ=37° в сторону отставания от вектора фазного напряжения ; под углом φВ=37° в сторону отставания от вектора фазного напряжения  откладываем вектор тока откладываем вектор тока  . .
Вектор тока  совпадает по направлению с вектором фазного напряжения совпадает по направлению с вектором фазного напряжения  так как φС=0. так как φС=0.
Для определения тока в_нулевом проводе I0 складываем геометрически векторы токов  , ,  и и  . Из векторной диаграммы, пользуясь масштабом для токов, находим ток I0=34A. . Из векторной диаграммы, пользуясь масштабом для токов, находим ток I0=34A.
Пример 2: В каждую фазу трехфазной сети включили сопротивления так, как показано на рис. 8. Величины сопротивлений даны на рисунке3. Линейное напряжение сети U =220B.
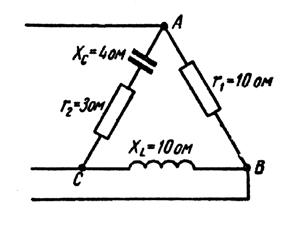
Рис. 8.
Определить: фазные и линейные токи, углы сдвига фаз, активную, реактивную и полную мощности трех фаз. Построить в масштабе векторную диаграмму.
Решение 1. Полные сопротивления фаз:
  
2. Углы сдвига фаз:
  (отстающий); (отстающий);
 (опережающий). (опережающий).
3. Фазные токи:



4. Активная мощность потребляется только активными сопротивлениями. Поэтому активная мощность трех фаз

5. Реактивная мощность потребляется только реактивными сопротивлениями. Поэтому реактивная мощность трех фаз

6. Полная мощность трех фаз

7. Для определения линейных токов строим векторную диаграмму (рис. 4). Построение _начинаем с векторов фазных (линейных) напряжений  , ,  и и  . .
Вектор тока  совпадает с вектором фазного напряжения совпадает с вектором фазного напряжения  , так как φАВ=0. , так как φАВ=0.
Вектор тока  отстает от вектора отстает от вектора  на угол φВС =90°, а вектор тока на угол φВС =90°, а вектор тока  опережает вектор опережает вектор  на угол φВС =53° . на угол φВС =53° .
Линейные токи  , ,  и и  на диаграмме равны геометрической разности соответствующих фазных токов. Например, на диаграмме равны геометрической разности соответствующих фазных токов. Например,  , т.е. ток в линейном проводе А равен геометрической сумме вектора фазного тока , т.е. ток в линейном проводе А равен геометрической сумме вектора фазного тока  и обратного вектора фазного тока и обратного вектора фазного тока . .
Из векторной диаграммы графически, пользуясь масштабом, определяем линейные токи: IA=66A; IB=43A; IC=25A.
Пример 3. Обмотки трехфазного генератора соединены по схеме “звезда”, э.д.с. в них 220 В. Построить векторные диаграммы и определить линейные напряжения для схемы соединения, в которой в одной точке сходятся: a) X Y Z б) X B Z в) X B C . Начала обмоток – A,B,C, концы обмоток – X,Y,Z. Принять нагрузку на генераторе равной нулю.
а) Для данной схемы соединения векторная диаграмма будет выглядеть следующим образом
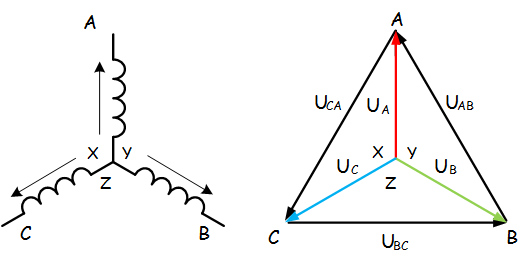
Линейные напряжения в данном случае будут равны и определяться как
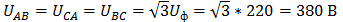
б) Так как обмотка BY подключена началом в нейтральную точку, то вектор напряжения оказывается повернутым на 180 относительно нормального положения.
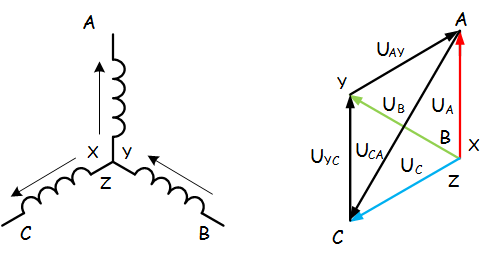
Линейные напряжения в данном примере будут разными по значению
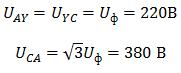
в) В данном случае относительно нормального положения повернуты вектора двух обмоток – BY и CZ.
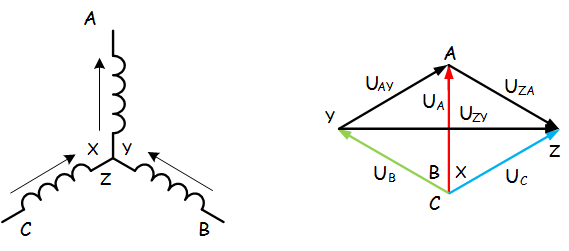
Как и в предыдущем примере, линейные напряжения не будут равны
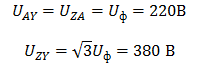
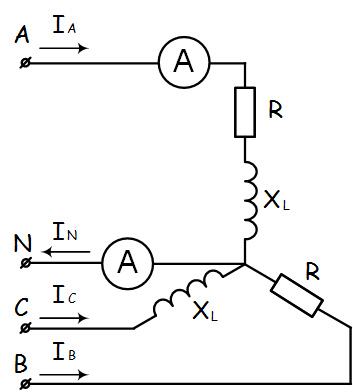
Пример 4. К зажимам приемника подсоединён трехфазный генератор, как показано на схеме. Определить показания амперметров A1,A2 и фазные токи зная, что Uл=380В, R=50 Ом, xL=35 Ом.
Определим комплексные значения сопротивления (для удобства вычислений будем переводить в показательную форму)
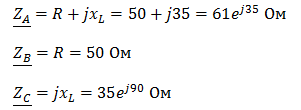
Напряжения в фазах будет равно
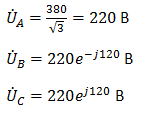
Токи в фазах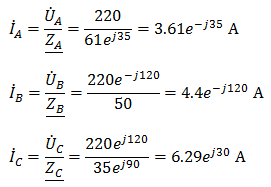
Ток в нейтральном проводе равен (для удобства сложения сначала переведем из показательной формы в алгебраическую, а затем наоборот)
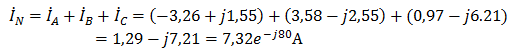
Соответственно, показания амперметров будут следующими:
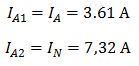
Пример 5. К зажимам приемника, подсоединён трехфазный генератор, обмотки которого соединены по схеме “треугольник”. Определить фазные и линейные токи, показания вольтметра, зная, что линейное напряжение равно 220 В, R=25 Ом, xL=xC=10 Ом.
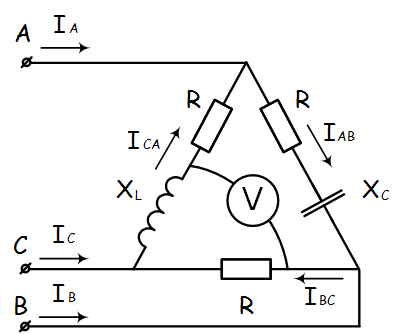
Как и в предыдущей задаче, в первую очередь определим комплексы сопротивлений
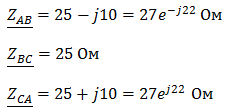 Фазное напряжение при данном соединении будет равно линейному, следовательно Фазное напряжение при данном соединении будет равно линейному, следовательно
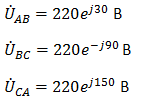 Фазные токи при несимметричной нагрузке не равны Фазные токи при несимметричной нагрузке не равны
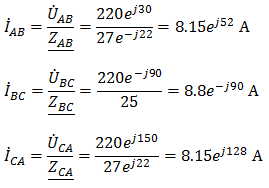
Для определения линейных токов представим фазные токи в алгебраической форме комплексного числа
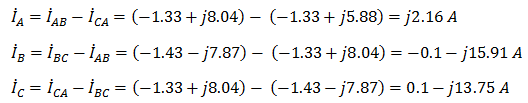
Сумма линейных токов
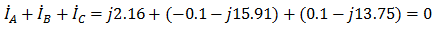
Равенство нулю суммы линейных токов является свойством любой трёхфазной системы.
Чтобы определить показания вольтметра, найдём сумму падений напряжения на xL и R в соответствующих обмотках.
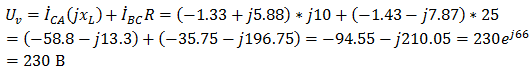 Т Т
Так решаются задачи на трехфазные цепи.
Практическая работа.
РАСЧЕТ ТРЁХФАЗНЫХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА
ВАРИАНТ 1
1.Потребитель трехфазного тока с несимметричной нагрузкой включен по схеме треугольник в сеть с линейным напряжением 220В. В каждой фазе включены последовательно активное и емкостное сопротивления, величины которых равны:
Фаза А: RА= 16 Ом, ХсА = 4 Ом
Фаза В: RВ= 4 Ом, ХсВ = 12 Ом
Фаза С: RС= 6 Ом, ХсС = 10Ом
Определить активную, реактивную и полную мощности потребителя
2. Фазное напряжение генератора 380В, сопротивление фаз приемника ZA= RА =ZВ= RВ = ZС = RС = 22 Ом. Определить ток в нулевом проводе
3.Электродвигатель трехфазного тока, соединенный звездой включен в сеть с напряжением 220 В. Мощность двигателя 12кВт, коэффициент мощности равен 0,98, коэффициент полезного действия 92,5%. Определить ток двигателя.
ВАРИАНТ 2
1.Потребитель трехфазного тока с несимметричной нагрузкой включен по схеме звезда в сеть с линейным напряжением 220В. В каждой фазе включены последовательно активное и емкостное сопротивления, величины которых равны:
Фаза А: RА= 16 Ом, ХсА = 4 Ом
Фаза В: RВ= 4 Ом, ХсВ = 12 Ом
Фаза С: RС= 6 Ом, ХсС = 10Ом
Определить активную, реактивную и полную мощности потребителя
2. Фазное напряжение генератора 380В, сопротивление фаз приемника ZA= RА =11Ом; ZВ= RВ = ZС = RС = 22 Ом. Определить ток в нулевом проводе
3.Электродвигатель трехфазного тока, соединенный звездой включен в сеть с напряжением 380 В. Мощность двигателя 12кВт, коэффициент мощности равен 0,98, коэффициент полезного действия 92,5%. Определить ток двигателя.
ВАРИАНТ 3
1.Потребитель трехфазного тока с несимметричной нагрузкой включен по схеме треугольник в сеть с линейным напряжением 220В. В каждой фазе включены последовательно активное и индуктивное сопротивления, величины которых равны:
Фаза А: RА= 6 Ом, ХLА = 14 Ом
Фаза В: RВ= 6 Ом, ХLВ = 12 Ом
Фаза С: RС= 6 Ом, ХLС = 10Ом
Определить активную, реактивную и полную мощности потребителя
2. Фазное напряжение генератора 440В, сопротивление фаз приемника ZA= RА =ZВ= RВ = ZС = RС = 18 Ом. Определить ток в нулевом проводе
3.Электродвигатель трехфазного тока, соединенный звездой включен в сеть 380В. Мощность двигателя 3000 Вт, коэффициент мощности равен 0,98, ток двигателя 5А. Определить коэффициент полезного действия
ВАРИАНТ 4
1.Потребитель трехфазного тока с несимметричной нагрузкой включен по схеме звезда в сеть с линейным напряжением 220В. В каждой фазе включены последовательно активное и индуктивное сопротивления, величины которых равны:
Фаза А: RА= 16 Ом, ХLА = 4 Ом
Фаза В: RВ= 4 Ом, ХLВ = 12 Ом
Фаза С: RС= 6 Ом, ХLС = 10Ом
Определить активную, реактивную и полную мощности потребителя
2. Фазное напряжение генератора 380В, сопротивление фаз приемника ZA= RА =11Ом; ZВ= RВ = ZС = RС = 22 Ом. Определить ток в нулевом проводе
3.Электродвигатель трехфазного тока, соединенный звездой включен в сеть с напряжением 220 В. Мощность двигателя 40 кВт, коэффициент мощности равен 0,94, коэффициент полезного действия 88,5%. Определить ток двигателя. |
|
|
 Скачать 1.97 Mb.
Скачать 1.97 Mb.













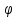 от векторов ,соответствующих фазных напряжений ( нагрузку считаем индуктивной).
от векторов ,соответствующих фазных напряжений ( нагрузку считаем индуктивной).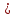 0, а фазные напряжения остаются неизменными.
0, а фазные напряжения остаются неизменными.


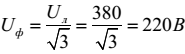 Поэтому выбираем схему соединения звездой.
Поэтому выбираем схему соединения звездой. 
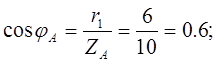
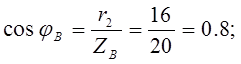
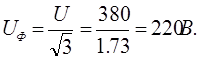
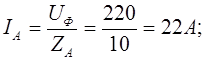
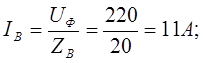
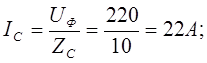


 (опережающий).
(опережающий).




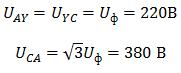

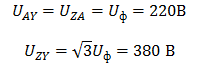

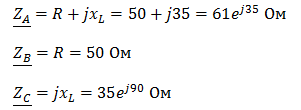
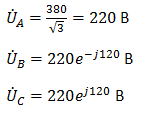
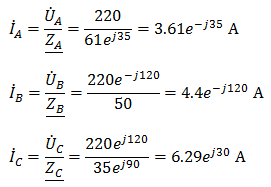
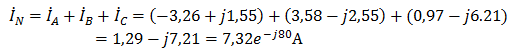
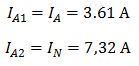

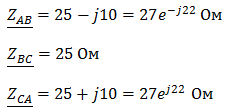 Фазное напряжение при данном соединении будет равно линейному, следовательно
Фазное напряжение при данном соединении будет равно линейному, следовательно 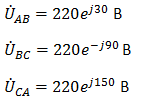 Фазные токи при несимметричной нагрузке не равны
Фазные токи при несимметричной нагрузке не равны 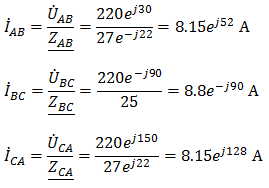
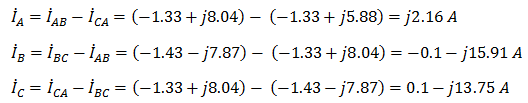
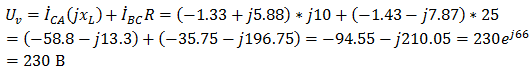 Т
Т