Курсовая работа. Основы инфокоммуникационных технологий
 Скачать 0.52 Mb. Скачать 0.52 Mb.
|
|
Федеральное агентство связи федеральное государственное бюджетное образовательное учреждение высшего образования «Сибирский государственный университет телекоммуникаций и информатики» (СибГУТИ) 11.03.02 Инфокоммуникационные технологии и системы связи, профиль Сети связи и системы коммутации (заочная форма обучения) Расчет базовых параметров телекоммуникационных систем Курсовая работа по дисциплине «Основы инфокоммуникационных технологий» Выполнил: студент, гр. _______ / ____________ / «__»_________ 2018 г. (подпись) Проверил: Преподаватель / Мелентьев О. Г./ «__»_________ 2018 г. (подпись) Новосибирск 2018 Содержание Введение 4 1 Задание 1 6 2 Задание 2 12 3 Задание 3 19 4 Задание 4 24 Заключение 32 Библиография 33 Введение Технология передачи информации, возможно, в большей степени, чем любые другие технологии, оказывает влияние на формирование структуры мирового сообщества. Возможность доступа к важнейшим событиям, происходящим в мире, свидетельствует о могуществе сетей передачи данных, обеспечивающих мгновенную доставку неподверженной цензуре информации широкой мировой аудитории [1]. Благодаря возникновению и развитию сетей передачи данных появился новый, высокоэффективный способ взаимодействия между людьми. Первоначально сети использовались главным образом для научных исследований, но затем они стали проникать буквально во все области человеческой деятельности. При этом большинство сетей существовало совершенно независимо друг от друга, решая конкретные задачи для конкретных групп пользователей. В соответствии с этими задачами выбирались те или иные сетевые технологии и аппаратное обеспечение. Построить универсальную физическую сеть мирового масштаба из однотипной аппаратуры просто невозможно, поскольку такая сеть не могла бы удовлетворять потребности всех ее потенциальных пользователей. Одним нужна высокоскоростная сеть для соединения машин в пределах здания, а другим – надежные коммуникации между компьютерами, разнесенными на сотни километров. Тогда возникла идея объединить множество физических сетей в единую глобальную сеть, в которой использовались бы как соединения на физическом уровне, так и новый набор специальных "соглашений" или протоколов. Эта технология, получившая название internet, должна была позволить компьютерам "общаться" друг с другом независимо от того, к какой сети и каким образом они подсоединены [2]. Когда возникла задача создания сетей передачи данных для ЭВМ, естественным, прежде всего, было обращение к столетнему опыту работы с телеграфными сетями. Так, опыт работы с телеграфными сетями с промежуточным накоплением (переприем телеграмм с переносом перфоленты) пригодился при создании сетей передачи данных с коммутацией сообщений, а с сетями абонентского телеграфа – для создания сетей передачи данных с коммутацией каналов. Важную роль в развитии сетей передачи данных сыграл научно-технический прогресс. Он позволил в течение сравнительно небольшого периода времени перейти от бумажных перфолент и перфокарт к магнитным лентам, а затем к магнитным дискам, полупроводниковым и оптическим запоминающим устройствам [3]. Одновременно огромный скачок произошел в технике защиты передачи от помех. От простых способов обнаружения ошибок путем проверки перфоленты на четность числа пробитых в ней отверстий удалось перейти к высоконадежным кодам не только обнаруживающим, но и исправляющим ошибки. Самое же главное, была создана микроэлектронная база. Она позволила сделать сложную аппаратуру компактной и экономичной по расходу электроэнергии. Все это открыло возможности построения технических средств передачи с огромной скоростью и ознаменовало наступление новой эпохи развития документальной связи. Целью работы является решение задач, имеющие отношение к телекоммуникационным системам. Работа состоит из следующих задач: – определение количества информации, – исследование возможностей MathCad, – генерация двоичного массива с желаемыми вероятностными параметрами, – исследование различных видов модуляций. 1 Задание 1 Исходные данные к заданию: Самостоятельно сформировать рисунок, состоящий из цветных точек (не менее 600) четырех (или более) цветов. Определить алфавит дискретного источника Определить количество информации, приходящееся на одну точку каждого цвета. Определить общее количество объективной информации в рисунке. Определить среднее количество информации, приходящееся на одну точку в рисунке. Закодировать рисунок равномерным двоичным кодом. Определить количество затраченных двоичных элементов. Определить среднее количество информации, приходящееся на один двоичный элемент при равномерном кодировании. Закодировать этот же рисунок неравномерным двоичным кодом. Определить количество затраченных двоичных элементов. Определить среднее количество информации, приходящееся на один двоичный элемент при неравномерном кодировании. Определить среднюю длину кодовой комбинации. Сделать выводы. Решение. Составим программу MathCad, которая сформирует рисунок, состоящий из цветных точек размером 25×25 и в шкале RGB – цветов: 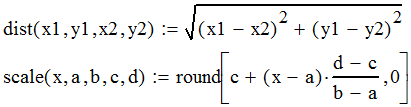 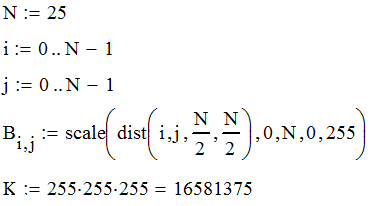 На рисунке 1.1 представлен сформированный рисунок.  Рисунок 1.1 – Рисунок размером 25×25 в шкале RGB – цветов. Определим алфавит дискретного источника. Под дискретным понимается источник, который в каждую единицу времени порождает один символ xi из дискретного множества А = {a1, a2, ..., ak}, называемого алфавитом источника, где k – размер алфавита. Источник, с точки зрения теории информации, считается заданным полностью, если известен не только алфавит источника, но и есть его модель, позволяющая вычислить вероятность любой последовательности символов в любой момент времени. Шкала RGB имеет 255 оттенков. Тогда размет алфавита равен 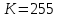 . .Определим количество информации, приходящееся на одну точку каждого цвета Количество информации можно рассматривать как меру уменьшения неопределенности знания при получении информационных сообщений. Подход к информации как мере уменьшения неопределенности знания позволяет количественно измерять информацию. Существует формула, которая связывает между собой количество возможных информационных сообщений К и количество информации I, которое несет полученное сообщение: Количество информации для событий с различными вероятностями определяется по формуле [3]: 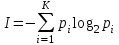 , (1.1) , (1.1)где I – количество информации, K – количество возможных оттенков, pi – вероятности отдельных событий. Если события равновероятны, то количество информации определяется по формуле [4]: 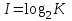 , (1.2) , (1.2)Тогда 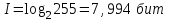 Определим общее количество объективной информации в рисунке. Количество информации, которое несет один знак алфавита, тем больше, чем больше знаков входит в этот алфавит. Количество знаков, входящих в алфавит, называется мощностью алфавита. Количество информации (информационный объем), содержащееся в сообщении, закодированном с помощью знаковой системы и содержащем определенное количество знаков (символов), определяется с помощью формулы: 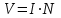 , (1.4) , (1.4)где I – информационный объем одного символа (знака); N – количество символов (знаков). Тогда 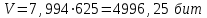 . .Определим среднее количество информации, приходящееся на одну точку в рисунке. Среднее количество информации H, которое приходится на один символ источника сообщений можно найти усреднением по всему объему алфавита [5]:  (1.5) (1.5)где pi – вероятности отдельных событий. Если события равновероятны, то среднее количество информации определяется по формуле:  . (1.6) . (1.6)Тогда  Закодируем рисунок равномерным двоичным кодом. На рисунке 1.2 представлена таблица значений десятичных кодов цветов (часть таблицы – верхний левый угол). Поскольку рисунок симметричен по горизонтали и по вертикали, то в дальнейшем также представлять коды цветов в том же виде.  Рисунок 1.2 – Таблица значений десятичных кодов цветов (часть таблицы – верхний левый угол). При двоичном равномерном кодировании для представления кода цвета достаточно 8-и бит. Определим среднее количество информации, приходящееся на один двоичный элемент при равномерном кодировании, при помощи формулы:  (1.6) (1.6)где Y – количество бит для представления оттенка, K – количество возможных оттенков. Тогда  . .Закодируем рисунок неравномерным двоичным кодом. С помощью программы mathCad определим неравномерный двоичный код для представления картинки. На рисунке 1.3 представлена таблица значений двоичных неравномерных кодов цветов (часть таблицы – верхний левый угол).  Рисунок 1.3 – Таблица значений двоичных неравномерных цветов (часть таблицы – верхний левый угол). Определить среднюю длину кодовой комбинации. Из таблицы видно, что – для 4-х элементов достаточно 3-х бит, – для 28-и элементов достаточно 5-и бит, – для 88-и элементов достаточно 6-и бит, – для 364-и элементов достаточно 7-и бит, – для 141-и элементов достаточно 8-и бит. Средняя длина определяется как среднее арифметическое с весовыми коэффициентами:  Таким образом, для неравномерного кодирования достаточно 7 бит. Определим среднее количество информации, приходящееся на один двоичный элемент при неравномерном кодировании: 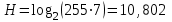 . .Вывод: При неравномерном кодировании избыточность кодирования уменьшается на 0,192 бит. 2 Задание 2 Исходные данные к заданию: Построить на оси времени график трех периодов синусоидальной функции s1(t) = sin(2π∙t/T) Построить на том же рисунке графики функций s2(t) = sin(2π∙t/T+φ) и s3(t) = s1(t)+s2(t). Изменяя сдвиг фаз в диапазоне φ=0..2∙π, исследовать поведение функций s2(t) и суммы s3(t). Что происходит с функцией s2(t) относительно s1(t) и с амплитудой s3(t) при изменении фазы. Сделать выводы. Сделать анимацию рисунка используя возможности MathCad: – определить переменную, которая будет изменяться для каждого кадра φ=FRAME – выбрать Инструменты/Анимация/Запись. – Настроить начальное и конечное значение переменной FRAME в окне «Запись анимации». Здесь же при необходимости можно изменять количество кадров в секунду. – выделить анимируемый график и нажать кнопку анимировать. Теорема косинусов. Определить длину результирующего вектора при сложении двух единичных векторов по правилу параллелограмма. Записать выражение для длины результирующего вектора от угла между складываемыми векторами. 6. В полярных координатах построить график зависимости длины результирующего вектора от угла в диапазоне φ=0..2π. Сравнить длины результирующего вектора и амплитуды суммы двух гармонических функций S(t) при одинаковых углах φ. Сделать выводы. Решение Построим на оси времени график трех периодов синусоидальной функции: 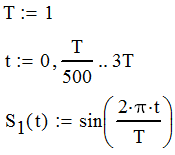 На рисунке 2.1 представлен график трех периодов синусоидальной функции. 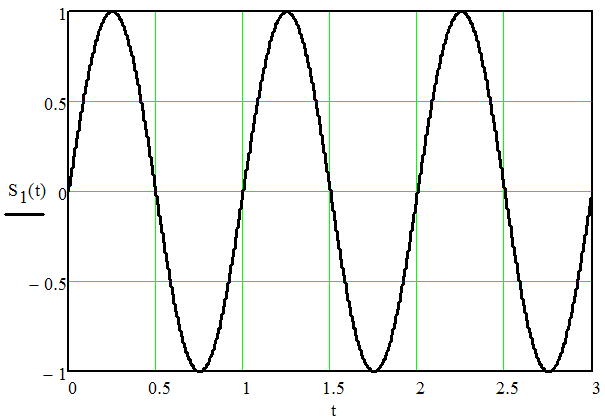 Рисунок 2.1 – График трех периодов синусоидальной функции. Построим на том же рисунке графики функций с фазовым сдвигом. 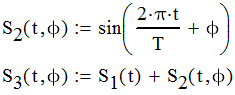 На рисунке 2.2 представлены графики синусоидальных функций и их суммы.  Рисунок 2.2 – Графики синусоидальных функций и их суммы Исследуем функции при изменении начальной фазы. На рисунке 2.3 представлены графики синусоидальных функций при различных значениях начальной фазы.  Рисунок 2.3 – Графики синусоидальных функций при различных значениях начальной фазы. Как видно из представленных графиков, при изменении начальной фазы, функция смещается. На рисунке 2.4 представлены графики сумм при различных значениях начальной фазы одной из функций.  Рисунок 2.4 – Графики сумм при различных значениях начальной фазы одной из функций Как видно из графиков сумм, максимальная амплитуда графика суммы наблюдается при совпадении начальных фаз синусоидальных функций. Если разница начальных фаз равна π (противофазные сигналы), то сумма графиков будет равна нулю. Анимация рисунка. Ниже представлен листинг для анимации синусоидальных функций и их суммы:  На рисунке 2.5 представлено окно задания параметров анимации [6].  Рисунок 2.5 – Окно задания параметров анимации В файле «Animate.avi» сохранена анимация. Определиv длину результирующего вектора при сложении двух единичных векторов по правилу параллелограмма: Правило параллелограмма- если два неколлинеарных вектора a и b привести к общему началу, то вектор с=а+b совпадает с диагональю параллелограмма, построенного на векторах a и b (рисунок 2.6). Причем начало вектора c совпадает с началом заданных векторов.  Рисунок 2.6 – правило параллелограмма Для нахождения суммы векторов необходимо: Отложить от точки A вектор АВ равный а и вектор АС равный b; Достроить фигуру до параллелограмма и провести диагональ; Диагональ параллелограмма – это сумма векторов. Выражение для длины результирующего вектора от угла между складываемыми векторами определяется по формуле:  Ниже представлен листинг для расчёта результирующего вектора при сложении двух единичных векторов по правилу параллелограмма:  На рисунке 2.7 представлен график зависимости длины результирующего вектора от угла.  Рисунок 2.7 – График зависимости длины результирующего вектора от угла Вывод: Длина результирующего вектора равна амплитуде суммы двух гармонических функций при одинаковых углах. 3 Задание 3 Исходные данные к заданию: Составить блок-схему алгоритма и написать программу генерации двоичного массива заданной длины с желаемой вероятностью появления единиц. Проверить частоту появления единиц в сгенерированных массивах для разных массивов (10,100 и 1000 элементов). Сделать выводы. Повторить пункты 1 и 2 для массивов, сгенерированных функцией rbinom(100,l,p) Составить блок-схему и написать программу визуализации двоичного массива на оси времени при заданной длительности единичного элемента и количестве точек на единичном интервале Решение. Для начала нам потребуется само определение массива. Массив-структура данных в виде набора компонентов (элементов массива), расположенных в памяти непосредственно друг за другом. Построим блок-схему генерации двоичного массива (рисунок 3.1):  Рисунок 3.1 – Блок-схема генерации двоичного массива Теперь напишем программу генерации двоичного массива заданной длины с желаемой вероятностью появления единиц:  В данной программе n – количество элементов массива, p – вероятность появления единиц. Проверим частоту появления единиц в сгенерированных массивах при разных длинах массивов (10,100 и 1000 элементов) и одинаковой вероятности появления единиц (0,2): При длине массива равной 10 элементам и вероятности появления единиц 0,2 получим:  Частота появления единиц при заданных параметрах равна 0.2 Теперь изменим длину массива на 100 элементов:  Частота появления единиц при заданных параметрах равна 0.22 Теперь изменим длину массива на 1000 элементов:  Частота появления единиц при заданных параметрах равна 0.204 Отсюда можно сделать вывод: при увеличении длины массива, увеличивается точность значения частоты появления единиц. Повторим пункты 1 и 2 для массивов сгенерированных функцией rbinom[7]. Проверим частоту появления единиц в массивах при разных длинах массивов (n=10,100 и 100 элементов) и при одинаковой вероятности появления единиц p=0.2 (Рисунок 4.7): Установим длину массива на 10 элементов  Частота появления единиц при заданных параметрах равна 0.2 Изменим длину массива на 100 элементов:  Частота появления единиц при заданных параметрах равна 0.21 Изменим длину массива на 1000 элементов:  Частота появления единиц при заданных параметрах равна 0.206 Визуализируем двоичный массив на оси времени:   Рисунок 3.2 – Lвоичный массив на оси времени Вывод: 1) Функция rbinom выполняет те же задачи, что и программа для генерации двоичного массива, а это значит: что гораздо рациональнее будет использование функции rbinom, ведь она более экономична и затрачивает меньше времени на написание; 2) При визуализации двоичного массива на оси времени, график принимает вид прямоугольного импульса. 4 Задание 4 Исходные данные к заданию: Сгенерировать случайный двоичный массив из 12 элементов с вероятностью появления единицы равной 0,5 Составить блок-схемы и написать программы АМ, ЧМ и ФМ модуляторов для заданных периодов несущих частот, длительности единичного элемента и точек на единичном интервале. На одном графике времени вывести двоичный массив и модулированный сигнал для каждого вида модуляции. Познакомиться с функцией генерации случайной величины, распределенной по нормальному закону rnorm(m, n, р). Добавить к каждому отсчету модулированного сигнала случайную величину генератора rnorm(m, n, p) и вывести на графике. Величину среднеквадратического отклонения шума (р) рекомендуется менять в пределах от 0 до 5. Сделать выводы. Решение Модуляция – процесс изменения одного или нескольких параметров высокочастотного (несущего) колебания по закону низкочастотного(информационного) сигнала [8]. Модуляция переносит спектр исходного сигнала на частоту несущей или в любую точку диапазона и зеркально отображает. Сгенерируем случайный двоичный массив из 12 элементов с вероятностью единицы (p=0,5):  Составим блок-схемы и напишем программы для амплитудной (AM), частотной (ЧM) и фазовой (ФM) модуляций. Начертим блок-схему для амплитудного модулятора (рисунок 4.1):  Рисунок 4.1 – Блок-схема для амплитудного модулятора Напишем программу для амплитудного модулятора: 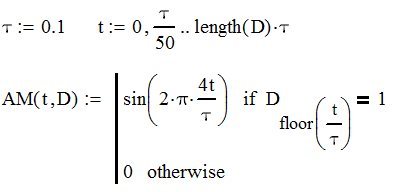 График амплитудной модуляции представлен на рисунке 4.2. 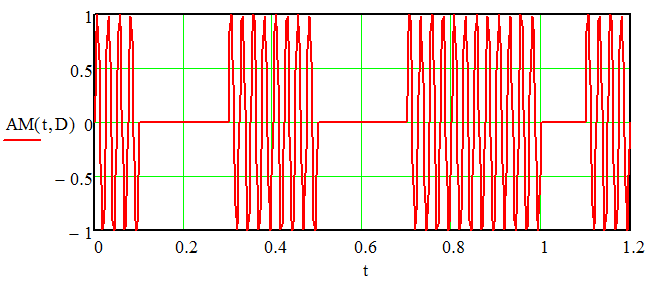 Рисунок 4.2 – Модулированный сигнал при амплитудной модуляции Начертим блок-схему для частотного модулятора (рисунок 4.3): 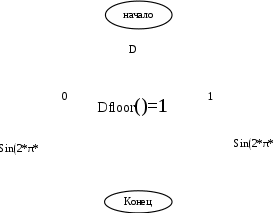 Рисунок 4.3 – Блок-схема для частотного модулятора Напишем программу для частотного модулятора: 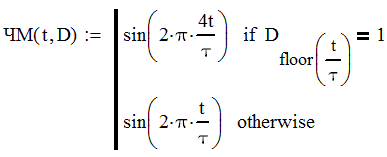 График частотной модуляции представлен на рисунке 4.4. 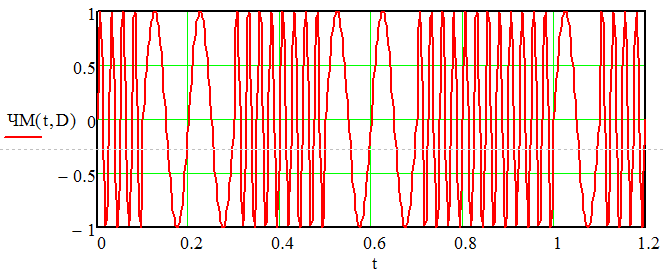 Рисунок 4.4 – Модулированный сигнал при частотной модуляции Начертим блок-схему для фазового модулятора (рисунок 4.5): 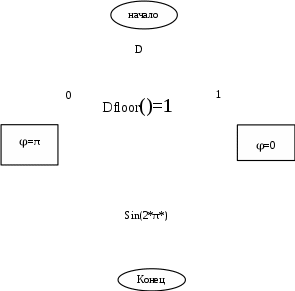 Рисунок 4.5 – Блок-схема для фазового модулятора Напишем программу для фазового модулятора: 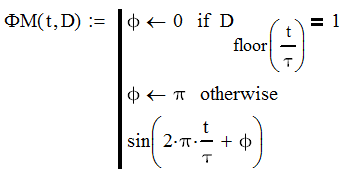 График фазовой модуляции представлен на рисунке 4.6.  Рисунок 4.6 – Модулированный сигнал при фазовой модуляции Далее понадобиться функция генерации случайной величины, распределённой по нормальному закону rnorm(L,m,ϭ). rnorm(L,m,ϭ) – вектор L независимых случайных чисел, каждое из которых имеет нормальное распределение [9]. Нормальное распределение, также называемое распределением Гаусса-Лапласа- распределение вероятностей, которое в одномерном случае задаётся функцией плотности вероятности. Добавим к каждому отсчёту модулированного сигнала случайную величину генератора rnorm(1,0,ϭ) и выведем на графике. ϭ – величина среднеквадратического отклонения шума. Шум-беспорядочные колебания различной физической природы, отличающиеся сложностью временной и спектральной структуры [10]. Добавим шум к амплитудной модуляции: 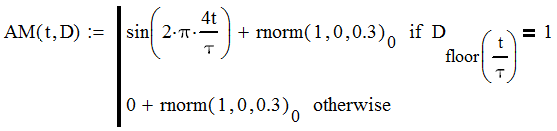 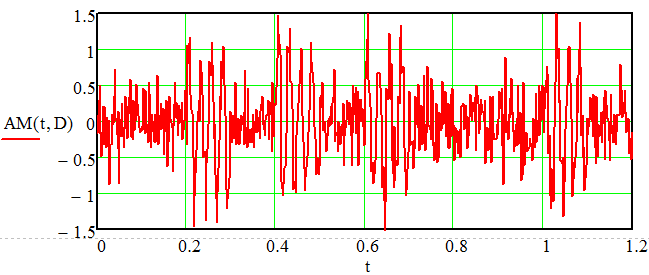 Рисунок 4.7 – Модулированный сигнал при амплитудной модуляции с шумом Добавим шум к частотной модуляции: 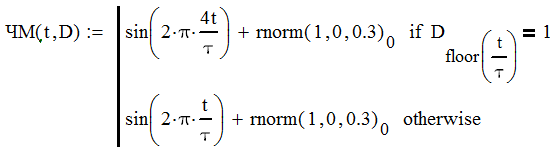 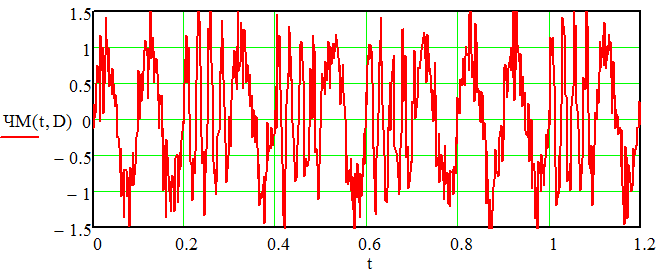 Рисунок 4.8 – Модулированный сигнал при частотной модуляции с шумом Добавим шум к фазовой модуляции: 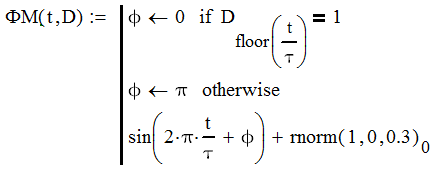 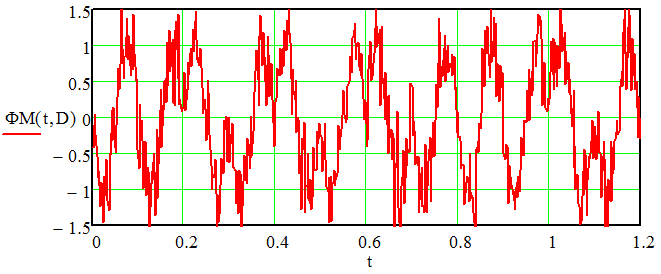 Рисунок 4.9 – Модулированный сигнал при фазовой модуляции с шумом. Вывод: Модуляция с шумом отображает условия, приближенные к реальным, ведь в обычной жизни передать сообщение без искажений невозможно, так как сществует огромное количество факторов создающих шум. Шум снижает качество передачи, так как сигнал в процессе искажается, а так же шум усложняет процесс приёма, потому что информационный сигнал гораздо сложнее выделить из модулированного колебания при присутствии шума. Заключение В результате выполнения работы решен ряд задач, которые имеющий отношение к телекоммуникационным системам, а именно – определено количество информации произвольного рисунка, – исследованы возможности MathCad, – сформирован двоичный массив с желаемыми вероятностными параметрами, – исследованы различные виды модуляций. Библиография Крук, Б. И. Телекоммуникационные системы и сети. Т.1. Современные технологии [Текст] : учеб. пособие / Б. И. Крук, В. Н. Попантонопуло, В. П. Шувалов. - М. : Горячая линия-Телеком, 2012. - 620с. Величко, В. В. Основы инфокоммуникационных технологий [Текст]: учеб. пособие / В.В. Величко, Г.П. Катунин, В.П. Шувалов; под ред. В.П. Шувалова. - М.: Горячая линия-Телеком, 2009. – 711с. Величко, В. В. Основы инфокоммуникационных технологий [Текст]: учеб. пособие / В.В. Величко, Г.П. Катунин, В.П. Шувалов; под ред. В.П. Шувалова. – М.: Горячая линия-Телеком, 2009. – 711с. Катунин Г.П. Основы инфокоммуникационных технологий [Электронный ресурс]: учебник / Г.П. Катунин. – Электрон. текстовые данные. – Саратов: Ай Пи Эр Медиа, 2018. – 797 c. – Режим доступа: http://www.iprbookshop.ru/74561 – ЭБС «IPRbooks» Олифер В.Г. Основы сетей передачи данных / В.Г. Олифер, Н.А. Олифер.- Интернет-университет информационных технологий, 2005. Никулин К.С. Математическое моделирование в системе Mathcad [Электронный ресурс]: методические рекомендации по выполнению контрольных работ по курсу «Компьютерное инженерное моделирование» / К.С. Никулин. — Электрон. текстовые данные. — М. : Московская государственная академия водного транспорта, 2009. — 65 c. — 2227-8397. — Режим доступа: http://www.iprbookshop.ru/46717.html. Королев В.Т. Математика и информатика. MATHCAD [Электронный ресурс]: учебно-методические материалы для выполнения практических занятий и самостотельной работы студентами специалитета/ Королев В.Т. – Электрон. текстовые даныные. – М.: Российский государственный университет правосудия, 2015. – 62 c. – Режим доступа: http://www.iprbookshop.ru/45224 – ЭБС «IPRbooks» Дьяконов В.П. Mathcad 8–12 для студентов [Электронный ресурс]/ Дьяконов В.П. – Электрон. текстовые данные.— М.: СОЛОН-ПРЕСС, 2005. – 632 c. – Режим доступа: http://www.iprbookshop.ru/20845 – ЭБС «IPRbooks» Основы современных компьютерных технологий: Учебное пособие/под ред. Хомоненко. – СПб.:КОРОНА, 2002. Основы современных компьютерных технологий. Ред. Хомченко А.Д. Острейковский В.А., Информатика, М., "Высшая школа", 2000 г.  |
