шпоры по СР. Основы теории упругости и виды моделей реальных сред
 Скачать 91.12 Kb. Скачать 91.12 Kb.
|
|
Особенности распределения скоростей (V-модель) осадочных пород Пермского края. Пермский край это типичный регион осадочного бассейна в пределах которого обычно находятся залежи углеводородов. Осадочный бассейн – это территория, которая достаточно долгое время подвергается опусканию, в ней накапливаются осадочные породы. Обычно в самом верху залегает некоторый слой, который называется зона малых скоростей (wz). Рис 3.4. Обычно змс ассоциируется с четвертичными породами. Потом идут Пермские породы до кунгура – терригенные, потом начинаются карбонаты с двумя прослоями терригенных. В соответствии с этим в Пермском крае выделяется ряд основных отражающих горизонтов, которые обычно приурочены к сменам литологии пород. Реальные среды являются горизонтально-слоистыми. Причем считается, что каждый слой является однородным, т.е. скорость в пределах каждого пласта не меняется. За исключением зоны малых скоростей, где меняется и скорость (от 300 м/с до 2000-2500 м/с) и мощность составляет от 5 до 50 м., остал |
Мы уже показали, что скоростное распределение связано с распределением времен и формой годографов, ну и в соответствии с уравнением Эйконала кинематика волн зависит от распространения скоростей в среде. При этом геологические среды аппроксимируются той или иной скоростной моделью, наиболее простой моделью является однородная среда, фронты волн в которой являются окружностями и считается, что в таких средах возникают и существуют объемные волны, т.е. в трехмерном пространстве их фронты волн являются сферами. В некоторых случаях в теории рассматриваются примеры распространения плоских волн. Эта аппроксимация вполне реальна, поскольку на больших расстояниях по сравнению с отрезком фронта волны, который рассматривается, объемные волны становятся плоскими. Если упругое полупространство реальных сред перекрывается слоем воздуха, то на свободной поверхности этого пространства в некотором слое пород возникают так называемые поверхностные волны. При этом объемные волны могут быть продольными и поперечными, поскольку эти колебания существуют совместно, при этом отличаясь скоростями. При этом продольных волн больше: 3.5. Процесс распространения волн подчиняется ряду принципов (законов или постулатов). 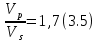 Принцип Ферма. Гласит, что форма сейсмического луча должна совпадать с траекторией пути, по которому время пробега волны от одной точки до другой минимально. Рис 3.5. С принципом Ферма связано и другое предположение, а именно предположение о принципе взаимности, согласно которому в однородных или близких к ним средах время распространения монотипной волны из одной точки в другую не измениться, если поменять местами источник и приемник. Принцип Гюйгенса. Именно на этом принципе решается задача построения фронтов волн даже в неоднородных средах. Этот принцип гласит: если имеется положение одного из фронтов волн и известно распределение скорости в среде, то мы всегда можем построить или восстановить положение предыдущего и последующего фронтов волн. Тем самым мы можем восстановить процесс распространения колебаний во всей среде. При чем на основе принципа Гюйгенса эти построения можно делать для любых типов и классов объемных волн как исходящих из источника (первичных), так и вторичных, которые возникают на границах раздела сред с разными скоростями. Т.е. рис 3.6. и тогда огибающая этих дуг окружностей даст положения предыдущего и последующего фронтов волн. Волновые уравнения типа 3.1. характеризуют колебания в тех точках среды, где отсутствуют источники колебаний или внешние силы/воздействия. Если появляется такой источник колебаний то в уравнении 1 вводиться некоторая сила Ф(x,y,z) как функция координат. При чем эта сила может быть суммой нескольких источников, решение нового уравнения при заданных начальных условиях обычно решается с использованием формул Пуассона, а если задаются некоторые граничные условия вне пространства, где действует функция Ф, то в этом случае используются формулы Кирхгофа для решения соответствующих уравнений. Френель сформулировал на основе принципов Гюйгенса подход к оценке размеров пространства, активно участвующий в передаче энергий волновых колебаний по пути от источника к точке наблюдения. |
В сейсморазведке используются упругие колебания, которые возбуждаются искусственно в какой-то точке среды, и распространяются во все стороны. Затем вблизи поверхности или в скважинах (горных выработках) регистрируются. Рис 4.1. Которые характеризуются некоторым периодом колебаний, временем прихода и частотой. Формулы 4.1. Комплексный спектр раскладывается на амплитудно-частотный спектр и фазово-частотный спектр. Таким образом в СР изучают волновое поле колебаний различных типов и классов. Причем в соответствии с волновым уравнением или уравнением Эйконала мы можем волновое поле представить и во временном виде и в пространственном виде. Если мы колебания регистрируем по оси Х, λ – длина волны, а k – волновое число (число длин волн в единице пространства) (4.2). 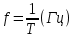 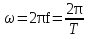 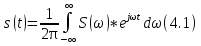 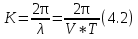 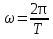 Где s(t) – колебание, S(ω) – комплексный спектр, который раскладывается на амплитудно-частотный спектр и фазо-частотный. Разнородность, разномасштабность и разнообразие задач, которые решает СР, связаны с применением различных типов и классов волн, которые при этом регистрируются в различных частотных диапазонах. Чаще всего классификация волн проводиться по трем основным признакам 1) по траектории движения (поляризации волн) колеблющихся частиц среды (продольные, поперечные и поверхностные). Среди поперечных волн выделяют SV (вертикальная плоскость) и SH (поперечные колебания в горизонтальной плоскости). В поверхностных волнах колебания происходят по эллипсу (есть горизонтальная и вертикальная компоненты; 2) показатель расхождения энергии волны по фронту. Волны могут быть объемными (сферическими рис 4.2). Если расстояние между источником и точкой регистрации достаточно большое, то можно сферические волны заменять плоскими (в некотором диапазоне), что упрощает решение различных практических и теоретических задач. Поскольку в данном случае сечение не меняется, лучи параллельны друг другу и форма колебаний не меняется S(t) – const. В некоторых случаях распространяющиеся волны считают цилиндрическими, ну например это делается при скважинных акустических исследованиях; 3) причинно-образовательный признак, который в сложных средах приводит к образованию различных классов волн. Например , если в упругой среде появляется акустически жесткая граница, то в этом случае возникают с одной стороны преломленные, а с другой стороны отраженные волны (рис 4.3). Т.е. часть энергии проходит вниз, часть отражается вверх. Если границ несколько, то каждая граница будет приводить к образованию отраженных и преломленных волн (рис 4.4). Помимо однократных волн, которые один раз отражаются или преломляются, у нас возникают многократные волны, которые несколько раз отражаются, иногда от одной и той же границы. Обычно они разделяются на полнократные и частичнократные (рис 4.5). Если скорость во втором слое больше, чем в первом, угол отражения может быть 90 градусов, наша волна возвращается к поверхности и появляется головная преломленная волна (рис 4.6). Если у нас скорость увеличивается с глубиной, то в этом случае возникает рефрагированная волна (4.7), т.е она сама постепенно возвращается к поверхности. Чем меньше угол наклона такой волны, тем глубже она проникает в геологическую среды. В сложных средах возникают смешанные классы волн, ну например отраженно-преломленные или преломлено-отраженные, отраженно-кратные-преломленные волны (рис 4.8). Отраженные волны, которые возникают на протяженных границах, иногда называются зеркальными или зеркально-отраженными. Считается, что в этом случае у нас площадка отражения (где свойства не меняются) гораздо больше, чем длина волны, которая распространяется в этой среде (рис 4.9). Если в среде имеются неоднородности, по размерам сопоставимые с длинной волны, то возникают дифрагированные волны (рис 4.10). Если же размеры неоднородности меньше, чем длина волны, то на таких неоднородностях возникают рассеянные волны. Такими мелкими неоднородностями могут служить наличие трещины в породе. Иногда в связи с изменением напряженности в горных породах возникают так называемые волны сейсмической эмиссии или микросейсмические колебания, которые тоже иногда используются для решения тех или иных задач. Имеются неоднородности, которые приводят к образованию обменных волн, т.е. волны, которые меняют свой тип p на s или s на p. | ||
Как мы уже видели, наиболее распространенным случаем в практике является модель слоистых сред, в которых имеются отражающие или акустически жесткие границы. В этом случае у нас в разрезе возникает как минимум одно или несколько границ, которые разделяют слои с различными физическими свойствами. Классическим примером является наличие одной границы, на которой меняются скорости волн и плотности. AI акустический импеданс или акустическая жесткость (4.3). Рис 4.11. 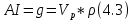 Отражающие границы возникают в том случае, когда изменяются акустические жесткости пластов, а это связано с изменением литологии или возраста соответствующих отложений. В этом случае если у нас есть граница, то возникают, отраженные и преломленные волны. Соответственно для этого случая можно написать закон отражения-преломления (4.4) 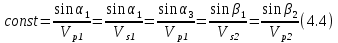 Отношение синуса угла к скорости это величина постоянная на данной границе. В связи с этим возникает такой вопрос: угол падения равен ли углу отражения. В силу закона отражения-преломления углы падения и преломления связаны со скоростями соответствующих типов волн. Если тип волны не меняется, то скорость распространения данной волны остается прежней и в этом случае угол падения должен быть равен углу отражения. Аналогично меняются и углы преломления. При угле падения = 0 или близких к ним углах у нас возникают только монотипные волны. При увеличении угла падения интенсивность обменных волн возрастает. Если падает поперечная волна на границу, то в этом случае возникают продольная и поперечная отраженные волны и продольные обменные волны преломленные во вторую среду. Если в качестве первичной волны падает SH волна, то возникает только SH отраженная и SH преломленная, обменных волн не возникает. |
Рассмотрим ту же самую границу, но случай возьмем, когда Vp1 При таком распределении скоростей V2>V1, возникают и отраженные и головные преломленные волны. Рассмотрим второй случай: пусть V1> V2. Рис 4.15. Тогда угол альфа будет больше, чем бета. В этом случае возникает с одной стороны отраженная волна, а с другой стороны возникает преломленная проходящая вниз волн. Головная преломленная волна возникать не будет. Необходимо также отметить, что в этом случае меняется фаза отраженной волны (рис 4.16). Происходит потеря полуволны, знак амплитуды меняется на обратный. Таким образом, отраженные волны возникают в случае, когда V1 не равно V2, или более точно AI1 не равен AI2. Головные преломленные волны возникают только в том случае, когда у нас V2>V1. |
Под динамикой обычно понимаются динамические особенности колебаний, куда входят амплитуда или энергия волн, их частотный состав, форма колебаний, траектория движения частиц среды и их изменения со временем или с расстоянием. Под кинематикой понимаются времена, связанные со скоростями и формы годографов. Сферические волны и сферическое или геометрическое расхождение волн Простейшей моделью среды является однородная модель, в которой возникают колебания от точечного источника, в этом случае волна распространяется во все стороны, ну и фронты волн будут иметь сферическую форму в пространстве (лучи – прямые линии). Рис 5.1. Если в этой среде выделить некоторый сферический луч, то в этом луче будет содержаться какая-то определенная энергия, которая будет зависеть от акустической жесткости среды, частоты колебаний и квадрата амплитуд этих колебаний (5.1): 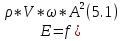 А – амплитуда колебаний, ω – частота. Причем площадь сечения (S1, S2, S3) будет возрастать и, соответственно, количество энергии на единицу площади будет уменьшаться. Этот процесс и называется сферическим или геометрическим расхождением волн. И даже в идеально упругих средах амплитуда колебаний с удалением или со временем будет как то убывать (рис 5.2). Если среда будет неоднородная, т.е. скорость волн меняется, то форма лучевой трубки тоже будет изменяться. Поскольку в сейсморазведке следующая модель это однородно-слоистая среда (в пределах пласта скорость одна и та же), в этом случае (рис 5.3) волна будет иметь не сферическую форму, а форму ломанной. Амплитуда в любом случае будет уменьшаться, т.к. она связана с изменением скоростей. Используя эти рассуждения, мы можем решать динамические задачи, т.е. как меняется амплитуда колебаний в различных средах с использованием «лучевого» метода. Хотя в этом случае у нас должно соблюдаться условие, что расстояния, для которых мы решаем задачи лучевым методом, должны быть гораздо больше длины волн. Отсюда следует вывод, что вблизи источника мы не можем решать задачу этим методом, поскольку будут большие погрешности. На больших расстояниях от ПВ волну можно считать плоской, в этом случае явления сферического расхождения не будет. |
Под динамикой обычно понимаются динамические особенности колебаний, куда входят амплитуда или энергия волн, их частотный состав, форма колебаний, траектория движения частиц среды и их изменения со временем или с расстоянием. Под кинематикой понимаются времена, связанные со скоростями и формы годографов. Неабсолютная упругость сред и явление поглощения в средах При изучении изменения амплитуд с расстоянием было замечено, что амплитуды колебаний уменьшаются гораздо в большей степени, чем это следует из расчетов геометрического расхождения волн. Отсюда делается вывод, что реальные среды не являются абсолютно упругими и за счет этого часть энергии волны переходит в другие формы энергии, и прежде всего, в тепловую. Такие неабсолютно упругие среды называются поглощающими или диссипативными. Это явление уменьшения амплитуд колебаний из-за неабсолютной упругости сред и называется поглощение. В физике существует несколько гипотез, объясняющих явление поглощения в реальных средах, исходя из разных механизмов преобразовании энергии. При чем, эти экспериментальные данные по изучению поглощения не всегда совпадают с теоретическими гипотезами. 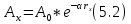 Теория упругого последействия (гипотеза Болцмана) и теория вязкого трения – две основных гипотезы. Первая гипотеза предполагает, что упругие напряжения не исчезают мгновенно при снятии напряжения, а существуют еще некоторое время, в связи с чем у нас и происходит уменьшение энергии распространяющихся волн. В теории вязкого трения энергия тратиться на трения между частицами, за счет чего происходит нагревание пород и часть упругой энергии превращается в тепловую. С учетом этого реальные среды являются поглощающими. А0 – амплитуда в начальной точке, α –коэффициент поглощения, rx – расстояние. Следует также отметить: обе теории происхождения искажения подчеркивают тот факт, что величина α зависит от частоты колебаний. А поскольку сейсмический импульс (рис 5.4) состоит из разных синусоид и косинусоид, их поглощение будет различным, причем высокочастотные колебания будет поглощаться быстрее, чем низкочасотная. Именно поэтому часто пишут, что α – частотно-зависимая функция. Рис 5.5. При этом поглощающими свойствами характеризуются как продольные, так и поперечные волны. Т.е мы можем говорить о коэффициентах поглощения продольных и поперечных волн αp<αs. Обычно в эффекты поглощения входит и изменение амплитуд колебаний за счет рассеяния энергии на мелких неоднородностях. Т.е. если у нас есть рыхлые или трещиноватые породы, у которых размеры пор или трещин гораздо меньше длин волн, то на таких неодноростях возникают рассеянные волны, т.е. часть энергии еще тратиться на образование рассеянных волн, которые приводят к уменьшению амплитуд колебаний. Существует так же в технике понятие «затухание», дак вот в этот термин вкладывается характер изменения амплитуд за счет воздействия нескольких факторов (геометрического расхождения, поглощения и рассеяния). Тогда как термин поглощение характеризует уменьшение амплитуды только за счет неидеальной упругости сред. При этом для низких частот и небольших удалений между ПВ и ПП потери на расхождение превышают потери на поглощение, а с увеличением частоты и уменьшением расстояния до нескольких километров, потери на поглощение растут и становятся преобладающими. Широко в практике используется понятие декремента поглощения, которое характеризует произведение α на длину волны λ (5.3). Декремент поглощения характеризует изменение амплитуд колебаний на расстоянии равном длине волны. 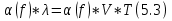 | |
