|
|
шпоры по СР. Основы теории упругости и виды моделей реальных сред
Основы теории упругости и виды моделей реальных сред.
Основы теории упругости – геологические основы сейсморазведки – динамические особенности и кинематические особенности распространения волн – форма и уравнения годографов.
Под кинематическими особенностями обычно подразумевают характер распределения фронтов волн или лучей и форму годографов, т.е. функций t(x) времени регистрации колебаний от удаления между ПВ (пункт возбуждения) и ПП (пунктом приема). Под динамическими особенностями обычно понимают характер изменения амплитуд, частот ну и соответственно формы регистрируемых колебаний.
Идея сейсморазведки: возбуждаем упругие колебания в ПВ, они расходятся во все стороны. Если имеются твердые среды, на которых изменяются физические свойства волн, то волны отражаются и преломляются. Головные волны и преломленные снова выходят к поверхности Земли. Поэтому теоретическую основу СР составляют знания о характере распространения упругих колебаний. Источником колебаний являются или взрывы или специальные ударные установки, иначе говоря, какие-то внешние силы (рис 1.1.). Эти внешние силы воздействуют соответственно на горные породы и стремятся изменить размеры и форму элементарных объемов среды. Иначе говоря, внешние силы приводят к созданию деформаций в среде, но каждая среда противопоставляет внешним воздействиям внутренние силы сцепления между частицами и соответственно стремиться возвратиться к своему первоначальному положению. Мерой изменения формы и размеров тел служит понятие относительных деформаций, свойство горных пород сопротивляться деформациям называется упругостью. Меру воздействия внешних сил на горные породы называют напряжением, т.е. величиной силы, действующей на единицу площади. Причем напряжения бывают нормальные и касательные (напряжения сдвига) (рис 1.2.). Когда сила действует под каким то углом к площадке, то обычно ее раскладывают на несколько компонент или составляющих этой силы. В данном случае мы можем изучать проекции или компоненты силы на соответствующие оси координат.
Возникающие в точке О (ПВ) напряжения и соответствующие им деформации распространяются в среде и создают процесс распространения колебаний. Для описания процесса распространения волн широко используется закон Гука, который устанавливает связь между напряжениями и деформациями среды. Вид этого закона зависит от сложности строения среды. Если эта связь линейна, что и наблюдается обычно в практике, когда напряжения и деформации являются небольшими, то такие тела принято называть идеально упругими или абсолютно упругими. В этом случае после прохождения колебаний среда возвращается в начальное состояние. Т.е. остаточные деформации отсутствуют. Если же напряжения возрастают выше предела упругости, то закон Гука не выполняется и связь между напряжениями и деформациями будет гораздо более сложной и такие тела называются пластическими или неабсолютно упругими. Такое происходит когда источником колебаний являются взрывчатые вещества. При работе с взрывчатыми веществами их заглубляют в скважину, чтобы не создавались поверхностные волны (рис 1.3.). В общем приближении геологические среды считаются абсолютно упругими. Вот с такой точки зрения абсолютно упругие среды часто подразделяют на изотропные и анизотропные. Породы отличаются по скорости прохождения волн и по плотности: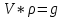 , где V – скорость, ρ – плотность, g – акустическая жесткость. Изотропные среды это когда свойства пород не зависят от направления. Анизотропные среды – это такие среды, где скорости упругих колебаний зависят от азимута (направления) их распространения (рис 1.4). Кроме того реальные среды могут быть однородные и неоднородные. В однородных. В однородных средах упругие свойства одинаковы во всех точках среды. В неоднородных средах свойства меняются. , где V – скорость, ρ – плотность, g – акустическая жесткость. Изотропные среды это когда свойства пород не зависят от направления. Анизотропные среды – это такие среды, где скорости упругих колебаний зависят от азимута (направления) их распространения (рис 1.4). Кроме того реальные среды могут быть однородные и неоднородные. В однородных. В однородных средах упругие свойства одинаковы во всех точках среды. В неоднородных средах свойства меняются.
В последние годы вводиться понятие дискретных сред (несплошных или прерывистых). В отличие от сплошных сред в дискретных средах свойства резко могут меняться от точки к точке. Чаще всего к дискретным средам относятся зернистые, трещиноватые или пористые породы. Таким образом в СР достаточно широко используются различные модели сред (рис 1.5). Чем сложнее модель, тем точнее мы можем описать реальную среду, но чем проще модель, тем удобнее с ней работать. Поэтому, выбор модели всегда является некоторым компромиссом между возможностью решить задачу точно и желанием решить ее быстро и легко. Понятно, что самая простейшая модель это однородная, изотропная, упругая, сплошная и наиболее широко используется в СР. Верхние модели таблицы описывают макроструктуру горных пород, а соответственно нижние в основном описывают микроструктуру.
|
Понятие напряжений и деформаций.
Чтобы рассчитать величины деформаций обычно устанавливают характер связи между напряжениями σ и деформациями ε. В основе теории СР лежит закон Гука, который и определяет связь между напряжениями и деформациями. Существуют нормальные и касательные напряжения. Для сжимающих или растягивающих напряжений и одномерной модели среды обычно закон Гука выглядит таким образом:
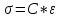
Где C – некоторый коэффициент пропорциональности, в качестве которых выступают некоторые физико-механические коэффициенты, ну например, модуль Юнга или коэффициенты Ламе. Если у нас имеются касательные напряжения τ, то в этом случае закон Гука выглядит таким же образом, но только в качестве коэффициента пропорциональности обычно выступает модуль сдвига. Для математического описания напряжений, возникающих в твердом теле, широко используется так называемый тензор напряжений, т.е. изображения вектора напряжения в некоторой системе координат. Для этого в каждой точке тела обычно рассматривается три вектора σx, σy, σz, каждая из которых раскладывается на три компоненты в зависимости от характера осей. Если обозначить Ux, Uy, Uz компоненты вектора смещения U, то можно написать для этих компонент:
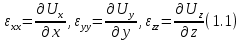
Сумма этих компонент будет нам давать объемную деформацию, которая называется дилотация θ.
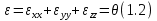
Соответственно сдвиговые деформации будут выражаться такими выражениями:
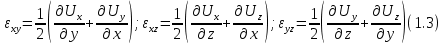
Если в этих формулах вместо +будет -, то они будут описывать поворот вокруг той или иной оси, например:
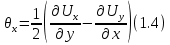
При этом надо отметить, что выражения 1.1 и 1.3 используются, когда деформации небольшие, поэтому их квадраты и произведения тоже являются очень маленькими и их можно не принимать в расчетах, т.е. считать равными нулю. И именно поэтому обычно считается, что смещение частиц среды являются линейными, что вполне применимо для СР.
|
Уравнение состояния среды.
В случае произвольных анизотропных упругих сред каждая компонента напряжения σij связана с компонентой деформации соответствующими модулями: 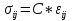 . Для трехмерного пространства эта связь в математической форме обычно записывается в матричной (табличной) форме в виде тензора: . Для трехмерного пространства эта связь в математической форме обычно записывается в матричной (табличной) форме в виде тензора:
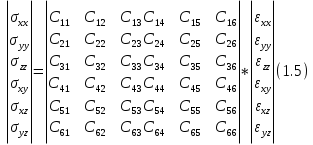
Если взять изотропную среду, то 24 коэффициента матрицы из 36 обращаются в нуль:
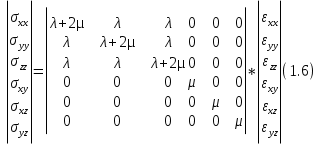
Если эти коэффициенты С заменить на соответствующие им константы Ламе λ (характеризует сопротивление среды сжатию-растяжению) и μ (характеризует сопротивление среды сдвигу). Если тензор заменить просто уравнениями, эти уравнения будут иметь такой вид:
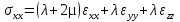
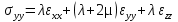
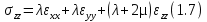
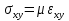
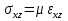
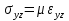
Где соответствующие напряжения связаны с деформациями с помощью констант Ламе. В одномерном варианте, т.е. для одной пространственной координаты, для изотропной среды, для нормальных и тангенсальных напряжений можно записать формулы: 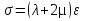 или или 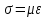 , которые можно считать, также как уравнения 1.7 и 1.6 уравнениями состояния среды и они как раз нам дают связь между напряжениями и соответствующими им деформациями. , которые можно считать, также как уравнения 1.7 и 1.6 уравнениями состояния среды и они как раз нам дают связь между напряжениями и соответствующими им деформациями.
|
Упругие модули, применяемые в теории сейсморазведки.
Для характеристики сред используются различные упругие константы или модули. В частности, модули Ламе μ и λ широко используются для описания объемных деформаций в теоретических исследованиях. Модуль μ выражает сопротивление среды сдвигу (жесткость к сдвигу), а λ характеризует сопротивление среды при чистом растяжении или сжатии. Широко в сейсморазведке также используются так называемые физико-механические или инженерные модули к которым относиться модуль Юнга E и коэффициент Пуассона ν. Модуль Юнга характеризует сопротивление при одноосном сжатии или растяжении. Коэффициент Пуассона ν характеризует отношении деформации к его удлинению под действием сил растяжения. Иногда говорят, что коэффициент Пуассона устанавливает соотношение между жесткостью к сдвигу и сопротивляемости среды к бессдвиговым деформациям. Обычно 0< ν<0,5. Причем, например, поскольку жидкости и газы не оказывают сопротивление сдвигу, то в этом случае коэффициент Пуассона максимален и равен 0,5, а коэффициент μ наоборот будет равен 0.
К-ты
|
Жесткие среды
|
Вода
|
Глина
|
μ
|
max
|
min
|
min
|
ν
|
min
|
max
|
max
|
Широко используются еще ряд модулей, например, используется коэффициент К (для объемных волн), который называется коэффициент всестороннего сжатия. Или 1/К – коэффициент сжимаемости среды. Используется модуль сдвига, который к однородных средах равен μ: G=μ. Иногда используют коэффициент М – несжимаемость для плоских волн. Также широко используется коэффициент γ: 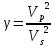 , он увеличивается для более жестких пород. Соответственно ν – это безразмерная величина, а все другие модули выражаются в единицах силы, деленных на площадь, т.е. в МПа. Причем существуют формулы, которые связывают все эти коэффициенты и для характеристики пород обычно используются какая-то пара из этих модулей. , он увеличивается для более жестких пород. Соответственно ν – это безразмерная величина, а все другие модули выражаются в единицах силы, деленных на площадь, т.е. в МПа. Причем существуют формулы, которые связывают все эти коэффициенты и для характеристики пород обычно используются какая-то пара из этих модулей.
|
Уравнения движения.
Уравнения состояния, которые были написаны на первой лекции, отображают статику среды, т.е. состояния равновесия, напряжения и деформаций. Если же к среде приложить какие-то напряжения (на каком-то участке или в точке), т.е. она выводиться из равновесия, возникают упругие колебания или волны, которые и распространяются в среде. Уравнения волнового движения, которые возникают к этом случае основываются на втором законе Ньютона (2.1).
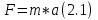
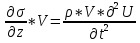
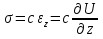
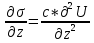
Уравнение движения связывает производные напряжения (если взять по оси z, то это будет 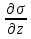 ) со второй производной от смещения по времени ) со второй производной от смещения по времени 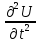 ). F будет равно производной σ на объем породы V, масса m будет равна плотности ρ * на объем породы V. Эти уравнения и называются уравнениями движения: ). F будет равно производной σ на объем породы V, масса m будет равна плотности ρ * на объем породы V. Эти уравнения и называются уравнениями движения:
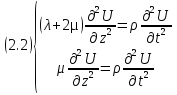
Причем первое уравнение характеризует реакцию среды на сжатие или растяжение, а второе уравнение характеризует касательное напряжение. Ну и соответственно, если перенести множители перед первым членом во вторую часть уравнения мы получим 2.3:
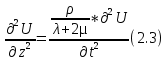
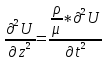
Эти формулы написаны для одномерного варианта, а не трехмерного. Из формул 2.4:
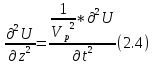
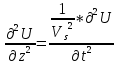
следует, что одновременно в средах возникает два типа смещений, это смещения сжатия – растяжения (продольных волн) или изменения формы и вращений (поперечных волн). В векторной форме, если через U обозначить вектор смещений, то соответственно 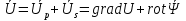 . В этом случае gradU это и есть вектор смещений , а rot Ψ– это уже вектор-потенциал поперечных смещений. Волновое уравнение в векторной форме запишется в виде 2.5: . В этом случае gradU это и есть вектор смещений , а rot Ψ– это уже вектор-потенциал поперечных смещений. Волновое уравнение в векторной форме запишется в виде 2.5:
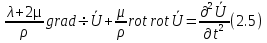
Таким образом уравнения 2.4 заменили в векторной форме одним уравнением 2.5.
|
Потенциал смещения и волновое уравнение.
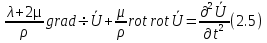
Как видно в формуле 2.5 в уравнении присутствуют два вида смещений продольные и поперечные волны. Чтобы уравнения не зависели от формы смещений, то вместо вектора смещений U, который определяет форму колебаний, часто используют потенциалов смещения. Если имеется потенциальная функция U, то 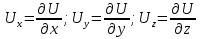 в этом случае волновое уравнение для продольных волн запишется в виде 2.6: в этом случае волновое уравнение для продольных волн запишется в виде 2.6:
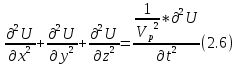
Соответственно, если ввести аналогичный потенциал для поперечных волн Ω, то мы будем иметь уравнение 2.7:
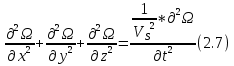
Соответственно эти уравнения 2.6 и 2.7 можно рассматривать и как уравнения движения и как волновое. Иногда волновое уравнение в сейсморазведке записывают в таком виде: 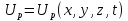 . При этом если подвергнуть это уравнение изменению, то оно будет иметь пару преобразования Фурье . При этом если подвергнуть это уравнение изменению, то оно будет иметь пару преобразования Фурье 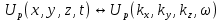 . k в данном случае волновые числа по соответствующим осям координат пространства.. Соответственно в частотной области мы получим дисперсионное соотношение 2.8: . k в данном случае волновые числа по соответствующим осям координат пространства.. Соответственно в частотной области мы получим дисперсионное соотношение 2.8:
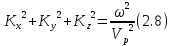
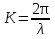
Из всех параметров, которые участвуют в написанных нами формулах, в сейсморазведке определяются только скорости. Поэтому когда говорят о модели среды в сейсморазведке – это в первую очередь модель распределения скоростей.
|
Кинематика волнового поля. Уравнение Эйконала.
Волновое уравнение определяет как кинематические, так и динамические характеристики полей упругих колебаний. С помощью волнового уравнения осуществляется переход от поля, которое задается в пространственной области среды к полю, существующему в области времени. При этом под кинематическими характеристиками колебаний подразумевают изменение времен прихода колебаний (форму их годографов), а под динамическими подразумевают интенсивность колебаний, их частотный состав, форму колебаний и даже характер смещения частиц (поляризацию волн). Под упругой волной обычно понимается некоторое возмущение, которое распространяется через заданную среду. При этом форма колебаний обычно считается неизменной (рис 2.2). Для удобства описания характера распространения колебаний обычно используется понятие лучей или фронтов волн. Фронт волны это положение начальной точки колебаний в различных направлениях, которые характеризуется одинаковым временем прихода колебаний. И как раз поверхность, которая соединяет эти одинаковые точки и называется фронтом волны. В закрашенной зоне на рисунке колебания существуют, а в идеальном случае на других участках колебаний нет. Таким образом если строить фронты волн в различные моменты времени, то мы можем описать характер распространения колебаний в пространстве. Иногда для описания используются лучи, которые являются нормальными к фронтам волн. При этом если среда однородная изотропная, то фронты волн будут являться окружностями, а лучи прямыми линиями. Если же среда не является однородной, то фронты волн могут иметь более сложную форму, а лучи могут быть криволинейными.
Повторение лекции: Рис 3.1. По оси х со скоростью V распространяется импульс на все большее расстояние. При этом колебание s(t) можно представить как сумму синусоидальных колебаний различных частот, фаз и амплитуд и различных времен вступлений:
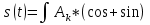
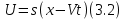
В трехмерном измерении U будет как функция координат и соответственно как сумма гармонических колебаний (3.3). tк – запаздывание относительно t. Если уравнение 3.3:
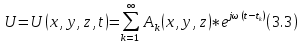
подставить в волновое уравнение (3.1):
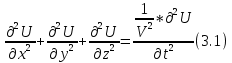
мы получим уравнение Эйконала, которое является основой геометрической сейсмики. И которое связывает времена пробега волн, которые изображаются фронтами, с координатами пространства, в каждой точке которого известна скорость распространения упругих колебаний. Слово Эйконал от греч – изображение или икона, поэтому уравнение Эйконала представляет собой как бы изображение характера распространения волн с помощью фронтов этих волн. Каждый член уравнения 3.1. должны разделить или умножить на 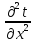 , тогда получим 3.4. – уравнение Эйконала, и фактически это уравнение отображает лишь кинематику волн: , тогда получим 3.4. – уравнение Эйконала, и фактически это уравнение отображает лишь кинематику волн:
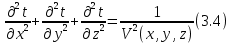
И из этого уравнения следует, что кривизна фронтов волн и лучей, с помощью которых как раз изображается характер распространения волн, в однородных и слабонеоднородных средах определяется единственным параметром среды, а именно распределением скорости. Левая часть уравнения 3.4. – распределение времени прихода волны, а правая – распределение скорости. В отличии от волнового уравнения здесь мы определяем только кинематические параметры. И нет данных о динамических особенностях волн (частоты, амплитуды, мощность сигнала).
Если среда однородная, то фронты волн будут иметь форму окружности, а лучи будут перпендикулярны фронтам волн и соответственно это будут прямые линии. Рис 3.2. Если среда будет неоднородная, то фронты волн будут иметь более сложную форму и сейсмические лучи в этом случае будут криволинейны. Рис 3.3. В соответствии с распределением скоростей меняется конфигурация фронтов и лучей. Обратная задача – получить распределении скоростей.
| | |
|
|
 Скачать 91.12 Kb.
Скачать 91.12 Kb.