Отражение и преломление плоских электромагнитных волн
 Скачать 240.5 Kb. Скачать 240.5 Kb.
|
|
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ ПЛОСКИХ ЭЛЕКТРОМАГНИТНЫХ ВОЛН 6.1. Основные теоретические сведения При распространении плоской электромагнитной волны в пространстве, представляющем собой области с различным значением параметров Комплексные амплитуды этих волн связаны с комплексной амплитудой падающей волны коэффициентами отражения и коэффициентами преломления (прохождения) Эти коэффициенты в каждом конкретном случае могут быть найдены на основании граничных условий на плоскостях, разделяющих среды с различными значениями электродинамических параметров. Могут быть также введены коэффициенты отражения и преломления для среднего значения плотности потока мощности: Если вектор Пойнтинга падающей волны перпендикулярен границе раздела, то где Выражение (6.1) аналогично формуле для коэффициента отражения по напряжению в линии передачи с волновым сопротивлением При наклонном падении направления распространения волн по отношению к границе раздела задаются углами, измеряемыми относительно нормали к этой границе. Плоскость, содержащая вектор Пойнтинга падающей волны и нормаль к границе раздела, называют плоскостью падения. Из граничных условий следует, что углы падения и законом Снеллиуса где индекс 1 относится к среде, содержащей падающую волну. С учетом выражения для коэффициента фазы Коэффициент отражения Если вектор 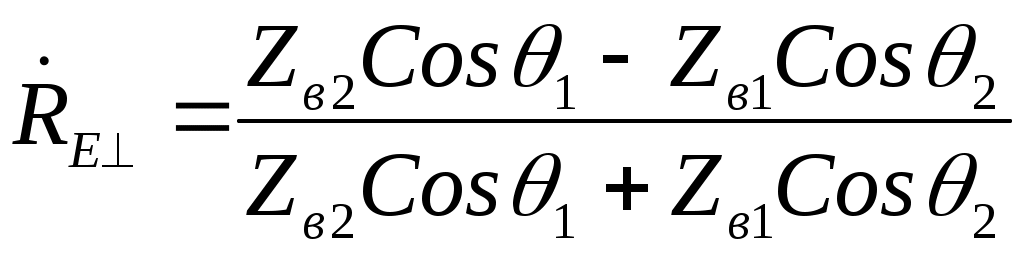 , (6.6) , (6.6)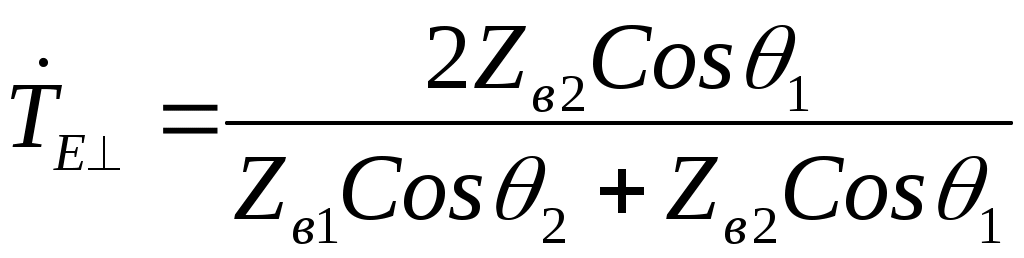 . (6.7) . (6.7)Выражения (6.4) – (6.7) при стремлении 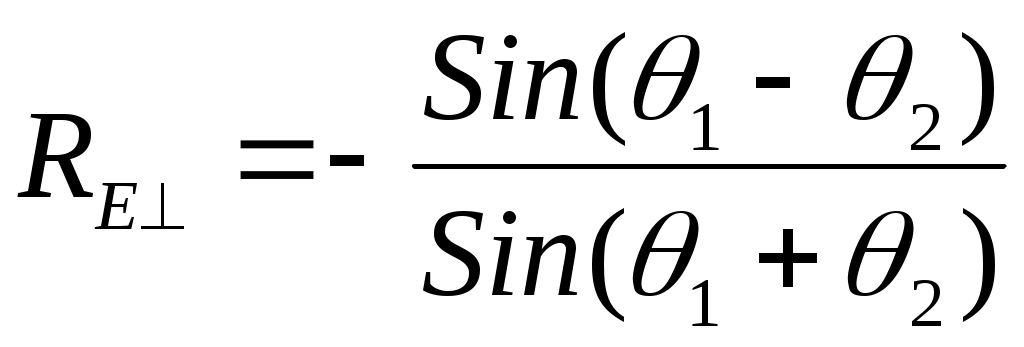 , (6.8) , (6.8)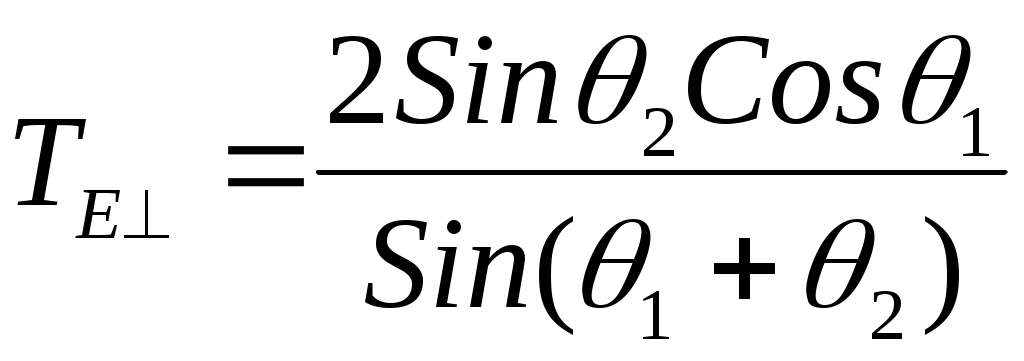 , (6.10) , (6.10)Во всех приведенных ранее формулах при необходимости можно исключить угол преломления Из формулы (6.9) следует, что при Согласно равенству (6.3) при то преломленная волна будет скользить вдоль границы раздела и в соответствии с выражениями (6.4), (6.6) коэффициенты отражения по модулю становятся равными единице. С дальнейшим увеличением угла падения модуль коэффициентов отражения остается равным единице будет изменяться только фаза коэффициентов 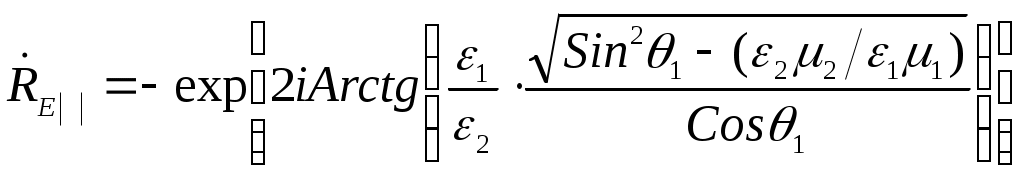 , (6.13) , (6.13)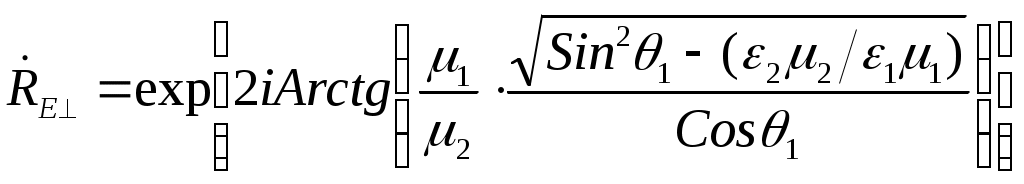 . (6.14) . (6.14)Коэффициенты преломления где 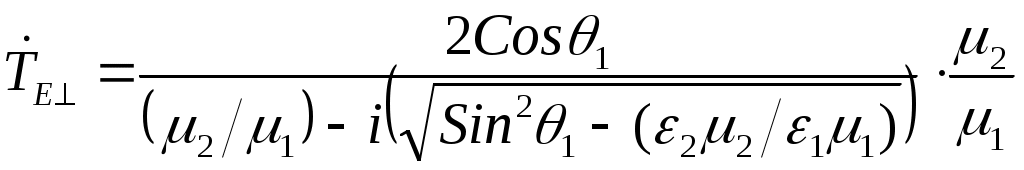 , (6.16) , (6.16)если вектор 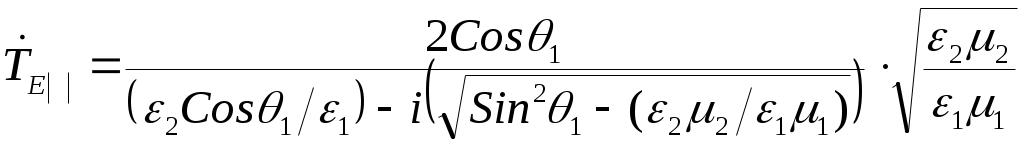 , (6.17) , (6.17)если вектор Если плоская электромагнитная волна падает под произвольным углом на границу раздела двух сред с потерями, то отраженную и преломленную волны следует считать неоднородными, поскольку плоскость равных амплитуд должна совпадать с границей раздела. Для реальных металлов угол между фазовым фронтом и плоскостью равным амплитуд мал (см. задачу 5.34), поэтому можно полагать, что угол преломления равен нулю. Это позволяет ввести приближенное граничное условие для реальных металлов (граничное условие Леонтовича): где В выражении (6.18) касательную составляющую вектора напряженности магнитного поля можно приближенно положить равной 6.2. Примеры решения типовых задач 6.1. Плоская электромагнитная волна падает нормально из вакуума на границу раздела со средой, имеющей параметры Определить комплексные коэффициенты отражения Решение. Учитывая, что Вычисления удобнее провести, используя приближенное выражение для корня квадратного так как При этом коэффициент отражения а коэффициент преломления С учетом полученного выражения для Переходя от комплексных амплитуд к мгновенным значениям, найдем 6.2. Измерения комплексного коэффициента отражения Определить параметры диэлектрика Решение. Комплексный коэффициент отражения от границы раздела между вакуумом и диэлектриком с параметрами откуда Подставляя в это выражение Производя вычисления, найдем 6.3. Плоская электромагнитная волна падает по нормали из вакуума на пластину диэлектрика без потерь толщиной Определить условия, при которых пластина становится прозрачной для падающей волны. Показатель преломления Решение. Формула для коэффициента отражения (6.1) аналогична по форме выражению для коэффициента отражения в теории линий передачи. Поэтому данной задаче может соответствовать схема замещения, изображенная на рис.6.1. 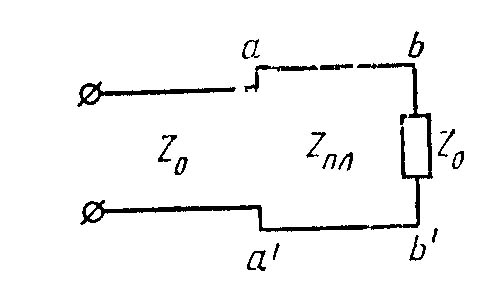 Рис.6.1. Отраженная от сечения или 6.4. Плоская электромагнитная волна падает под углом Вывести формулу для удельной мощности потерь Решение. Для определения удельной мощности потерь необходимо вычислить среднее значение вектора Пойнтинга, направленного внутрь металла. Если поля на поверхности металла известны, то Воспользуемся граничным условием Леонтовича (6.18), согласно которому Поскольку получим следующее выражение для удельной мощности потерь: Если для определения когда вектор напряженности магнитного поля падающей волны перпендикулярен плоскости падения, и когда вектор |
