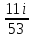матем решения2. Письменный экзамен по дисциплине Математика (2 курс спо) Пояснительная записка
 Скачать 46.24 Kb. Скачать 46.24 Kb.
|
|
Письменный экзамен по дисциплине «Математика» (2 курс СПО) Пояснительная записка Данный материал предназначен для проведения письменного экзамена по дисциплине «Математика» на втором курсе учреждений СПО. Задания составлены по темам и разделам высшей математики: математический анализ функций одной переменной, аналитическая геометрия на плоскости, линейная алгебра и решение систем линейных уравнений, нахождение математического ожидания и дисперсии случайных дискретных величин, заданных законом распределения. В данной статье не представлены задания по теории пределов. Экзамену предшествовала контрольная работа по данной теме, поэтому считаю возможным не дублировать этот материал. Для публикации представлены два варианта экзаменационной работы с ответами на каждое задание. Приведенные упражнения вычислительного характера позволяют проверить не только теоретические знания студентов, но и умения применять их на практике. Экзаменационная работа может быть использована преподавателями и студентами колледжей и учреждений СПО второго курса при изучении начал высшей математики, а также при подготовке к экзамену по дисциплине «Математика». Данные варианты экзаменационной работы были рассмотрены и утверждены на заседании предметно-цикловой комиссии естественно-научных дисциплин Государственного бюджетного профессионального образовательного учреждения Владимирской области «Юрьев-Польский индустриально-гуманитарный колледж». Письменный экзамен по дисциплине «Математика» (2 курс СПО) Вариант 1 1. Решить систему линейных уравнений методом Крамера: 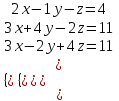 2. Вычислить определенный интеграл: 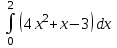 . .3. Вычислить интеграл методом подстановки: а) 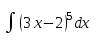 ; б) ; б) 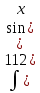 dx dx4. Найти объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями: 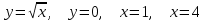 . .5. Скорость движения точки изменяется по закону 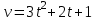 (м/с). Найти путь S, пройденный точкой за 8 секунд от начала движения. (м/с). Найти путь S, пройденный точкой за 8 секунд от начала движения.6. Найти производную функций: а) y =5 cosx ∙ sinx + 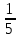 cos2x; б)y = 12x2 cos2x; б)y = 12x2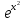 . .7. Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями в декартовых координатах: 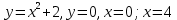 . .8. Исследовать средствами дифференциального исчисления функцию 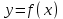 , если , если 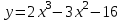 9. Даны точки А ( 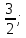 1; -2); В (2; 2; -3) и С (2; 0; -3) . Найдите длины сторон треугольника АВС и его периметр. 1; -2); В (2; 2; -3) и С (2; 0; -3) . Найдите длины сторон треугольника АВС и его периметр. 10. Найти математическое ожидание и дисперсию случайной дискретной величины, заданной законом распределения:
11. Даны два комплексных числа: z1 = 1+2i; z2 = 6 - 5i. Найти z1 + z2; z1 – z2; z1 ∙ z2; 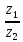 . .12. Вычислите: I6 + I20 + I30 + I36 + I54. 13. В классе 15 девочек и 11 мальчиков. Надо выбрать для дежурства 2 человека. Сколькими способами можно сделать выборку, если надо выбрать дежурных одного пола. 14. Составить уравнение прямой, проходящей через точку А(2; - 4) и пересекающей ось Ох под углом 45°. Вариант 2 1. Решить систему линейных уравнений методом Крамера: 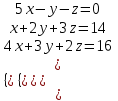 2. Вычислить определенный интеграл: 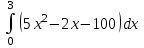 . .3. Вычислить интеграл методом подстановки: а) 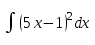 ; б) ; б) 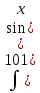 4. Найти объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями: 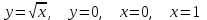 . .5. Скорость движения точки изменяется по закону 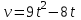 (м/с). Найти путь S, пройденный точкой за четвертую секунду. (м/с). Найти путь S, пройденный точкой за четвертую секунду.6. Найти производную функций: а) y = lnx2 - 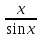 ;б) y = arctg 2 ;б) y = arctg 2 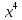 7. Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями в декартовых координатах: 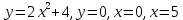 8. Исследовать средствами дифференциального исчисления функцию 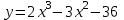 9. Определите вид треугольника АВС, если А (9; 3; - 5), В (2; 10; - 5), С (2; 3; 2). Найдите периметр треугольника АВС. 10. Найти математическое ожидание и дисперсию случайной дискретной величины, заданной законом распределения:
11. Даны два комплексных числа: z1 = 5 - 3i; z2 = 7 - 2i. Найти z1 + z2; z1 – z2; z1 ∙ z2; 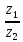 . .12. Вычислите: I8 + I13 + I48 + I100 + I501 13. В классе 13 девочек и 12 мальчиков. Надо выбрать для дежурства 4 учащихся. Сколькими способами можно сделать выборку, если надо выбрать 2 девочки и 2 мальчика. 14. Составить уравнение прямой, проходящей через две точки М1 (2;3) и М2 (-3;4). Ответы:
Критерии оценивания: каждое задание оценивается 1 баллом. Обязательные задания: №1, 2, 7, 8, 14. Оценка «2» - менее 5 баллов Оценка «3» - 5 баллов Оценка «4» - 7 баллов Оценка «5» - 9 баллов Время выполнения: 2 часа. |

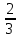
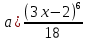 + C ; б)
+ C ; б)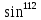 x + C
x + C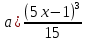 + C ; б)
+ C ; б)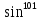 x + C
x + C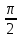
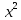 )
)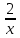 -
- 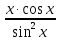 ; б)
; б) 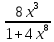
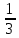 кв.ед
кв.ед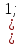 + ∞)
+ ∞) АВС - равносторонний , Р = 21
АВС - равносторонний , Р = 21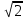
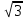
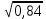
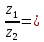 -
-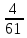 +
+ 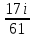
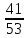 +
+