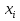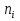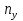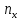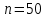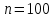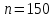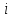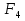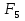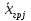Iндивiдуальнi та завдання для самостiйної роботиТЙМС. Основні поняття комбінаторики розміщення, перестановки, комбінації
 Скачать 51.01 Kb. Скачать 51.01 Kb.
|
|
Основні поняття комбінаторики – розміщення, перестановки, комбінації. Задачі для самостійного розв’язання. 1. У класі 7 учнів успішно навчаються математиці. Скількома способами можна вибрати з них двох для участі в математичній олімпіаді? 2. Учням дали список з 6 книг, що рекомендовано прочитати під час канікул. скількома способами учень може вибрати з них 6 книг? 3. У класі навчаються 16 хлопчиків і 12 дівчаток. Для прибирання території потрібно виділити 4 хлопчика та 3 дівчинки. Скількома способами можна це зробити? 4. Скількома різними способами збори, на яких присутні 40 осіб, можуть обрати з числа своїх учасників голову зборів, його заступника та секретаря? 5. З 12 членів туристичної групи потрібно вибрати трьох чергових. Скількома способами можна зробити цей вибір? 6. В одинадцятому класі 35 учнів. Вони обмінялися один з одним фотокартками. Скільки всього фотокарток було роздано? 7. Скількома способами можна розподілити уроки в шести класах між трьома вчителями, якщо кожний вчитель викладатиме у двох класах? 8. Спростити 9. Розв’язати рівняння
Дії з випадковими подіями. Індивідуальні завдання 1. Радіостанція аеропорту надсилає 3 повідомлення для екіпажу літака. Імовірність прийому екіпажем першого повідомлення дорівнює 0,6, другого — 0,65, третього — 0,7. Знайдіть імовірність того, що екіпажем прийнято: а) тільки одне повідомлення; б) принаймні одне повідомлення. 2. Аеропорт протягом доби виконує 3 рейси до міста А. Імовірність затримки першого рейсу через метеоумови дорівнює 0,05, другого — 0,1, третього — 0,15. Знайдіть імовірність того, що: а) тільки один рейс буде виконано із затримкою; б) усі рейси буде виконано вчасно. 3. Через метеоумови літак було відправлено на запасний аеродром, при наближенні до якого на його борту залишалось палива на З заходи на посадку. Імовірність посадки літака при першому заході дорівнює 0,8, при другому — 0,95, при третьому — 0,995. Знайдіть імовірність благополучної посадки літака. 4. Аеропорт протягом доби виконує 3 рейси. Імовірності повного комерційного навантаження для першого, другого і третього рейсу дорівнює відповідно 0,9; 0,85 і 0,8. Знайдіть імовірності того, що з повним комерційним навантаженням буде виконано: а) тільки 2 рейси; б) принаймні 2 рейси. 5. На кожному з трьох верстатів виготовлено по одній деталі. Імовірність браку на першому верстаті дорівнює 0,05, на другому — 0,07, на третьому — 0,1. Знайдіть імовірність того, що серед виготовлених деталей: а) тільки одна бракована; б) принаймні одна бракована. 6. На станції спостереження встановлено 4 радіолокатори різних конструкцій, які виявляють об'єкт незалежно один від одного. Імовірність виявлення об'єкта першим локатором дорівнює 0,86, другим — 0,9, третім — 0,92, четвертим — 0,95. Знайдіть імовірність виявлення об'єкта: а) тільки одним локатором; б) принаймні одним локатором. 7. Із аеропорту протягом доби виконуються 3 рейси. Імовірність повного комерційного навантаження для першого рейсу дорівнює 0,95, для другого — 0,9, для третього — 0,85. Знайдіть імовірність того, що з повним комерційним навантаженням буде виконано: а) лише один рейс; б) принаймні один рейс. 8. Диспетчер керує двома літаками, що заходять на посадку двох різних коридорів. Імовірність посадки літака без відходу на друге коло з першого коридору дорівнює 0,95, а з другого — 0,92. Знайдіть імовірність того, що а) обидва літаки здійснять посадку без відходу па друге коло; б) тільки один літак відійде на друге коло; в) принаймні один літак відійде на друге коло. 9. Технічна система складається з трьох пристроїв, які працюють незалежно один від одного. Імовірність виходу з ладу за певний час роботи для першого пристрою дорівнює 0,1, для другого і третього пристроїв ця ймовірність однакова і дорівнює 0,15. Знайдіть імовірність виходу з ладу за час роботи: а) тільки одного пристрою; б) двох пристроїв; в) принаймні одного пристрою. 10. З аеропорту протягом дня виконуються 3 рейси. Імовірність затримки через метеоумови для першого рейсу дорівнює 0,1, для другого — 0,15, для третього — 0,2. Знайдіть імовірність того, що із затримкою буде відправлено: а) тільки один рейс; б) принаймні один рейс. 11. Імовірність виготовлення виробу найвищої якості на першому верстаті становить 0,7, на другому — 0,8. На першому верстаті виготовлено 2 вироби, на другому — 3. Знайдіть імовірність того, що всі виготовлені вироби мають найвищу якість. 12. З аеропорту А до аеропорту В щодоби виконуються 3 рейси. Імовірність придбання квитка на перший рейс дорівнює 0,85, на другий — 0,9, на третій — 0,95. Замовлено квитки на кожний рейс. Знайдіть імовірність одержання квитка: а) тільки на один рейс; б) на 2 рейси; в) принаймні на один рейс. 13. Для повідомлення про аварію встановлено 3 сигналізатори, які працюють незалежно один від одного. Імовірність спрацьовування при аварії першого сигналізатора дорівнює 0,95, другого — 0,92, третього — 0,9. Знайдіть імовірності того, що при аварії спра цюють: а) тільки 2 сигналізатори; б) принаймні 2 сигналізатори. 14. Радіостанція аеропорту надсилає 3 повідомлення для екіпажу літака. Імовірність прийому екіпажем першого повідомлення дорівнює 0,9, другого — 0,95, третього — 0,98. Знайдіть імовірність того, що екіпажем прийнято: а) тільки 2 повідомлення; б) принаймні 2 повідомлення. 15. Відділ технічного контролю перевіряє деталі. Імовірність того, що деталь виявиться стандартною, дорівнює 0,9. Знайдіть імовірність того, що: а) із трьох перевірених деталей тільки одна буде нестандартною; б) четверта з перевірених деталей виявиться нестандартною. 16. Три контролери незалежно один від одного перевіряють якість приладу. Імовірність приймання приладу першим контролером дорівнює 0,95, другим — 0,9, третім — 0,85. Знайдіть імовірність приймання приладу: а) тільки одним контролером; б) принай мні одним контролером; в) усіма контролерами. 17. З двох гармат зроблено по одному пострілу по цілі. Імовірність тільки одного влучення при цьому дорівнює 0,46. Відомо, що ймовірність влучення в ціль для першої гармати дорівнює 0,7. Знайдіть імовірність влучення для другої гармати. ) Повна ймовірність. Формула Байєса, ймовірність гіпотез. Задачі для самостійного розв’язання. 1. На склад надійшли деталі з трьох верстатів. На першому верстаті виготовлено 40% деталей від їх загальної кількості, на другому - 35% і на третьому 25%, причому на першому верстаті було виготовлено 90% деталей першого сорту, на другому - 80% і на третьому - 70%. Яка ймовірність того, що навмання взята деталь виявиться першого сорту? 2. У першому ящику є 8 білих і 6 чорних куль, а в другому - 10 білих і 4 чорних. Навмання обирають ящик і кулю. Відомо, що вийнята куля - чорна. Знайти ймовірність того, що був обраний перший ящик.
Схема та формула Бернуллі Задачі для самостійного розв’язання.
Розв’язування завдань за модулем 1 Задачі для самостійного розв’язання.
3) 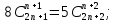 4) 13 4) 13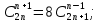 5) 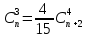 . .
Диференціальна та інтегральна функція розподілу Індивідуальні завдання Неперервну випадкову величину Х задано функцією розподілу 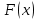 (щільністю ймовірності (щільністю ймовірності 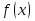 ). Знайти параметр А, щільність ймовірності ). Знайти параметр А, щільність ймовірності 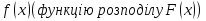 , числові характеристики , числові характеристики 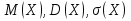 , ймовірність того, що випадкова величина Х у результаті випробування набуде можливого значення з інтервалу , ймовірність того, що випадкова величина Х у результаті випробування набуде можливого значення з інтервалу 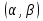 . .
Статистичні оцінки параметрів розподілу. Довірливий інтервал Задачі для самостійного розв’язання. 1. Вимірювання відхилень розрахункового часу польоту літака від фактичного дали такі результати, хв.:
Знайти точкові незміщені оцінки середнього значення і середньо квадратичного відхилення відхилень розрахункового часу польоту літака від фактичного. ( 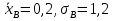 ) )2. У ВТК (відділ технічного контролю) було виміряно 400 валиків із партії, які виготовляє завод. Результати вимірювань, мм:
Знайти точкові незміщені оцінки середнього значення, виправленої дисперсії та середнього квадратичного відхилення розмірів валиків. 3. Побудувати інтервальний статистичний розподіл задачі 1 і знайти точкові незміщені оцінки середнього значення, виправленої дисперсії та середнього квадратичного відхилення випадкової величини, описаної в цій задачі. 4. Знайти довірчі інтервали та точність відповідних інтервальних оцінок для невідомого математичного сподівання нормально розподіленої випадкової величини Х, якщо 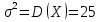 , обсяг вибірки n=36 i , обсяг вибірки n=36 i 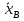 =7. Довірчі інтервали та відповідні їм точності побудувати для надійності γ=0,95; γ=0,99; γ=0,999. =7. Довірчі інтервали та відповідні їм точності побудувати для надійності γ=0,95; γ=0,99; γ=0,999.5. Залишок Х пального в баках літака після кожного з 15 рейсів за заданим маршрутом мав такі значення, кг:
Побудувати довірчий інтервал з надійністю γ=0,999 для математичного сподівання залишку пального в баках літака після рейсу, вважаючи, що залишок пального – нормально розподілена випадкова величина. Параметри лінії регресії. Задачі для самостійного розв’язання. Варіант № 1 Знайти вибіркове рівняння прямої лінії регресії X на Y за даними 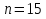 спостережень: спостережень:
Параметри лінії регресії Варіант № 2 Знайти вибіркове рівняння прямої лінії регресії X на Y за даними 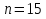 спостережень: спостережень:
Параметри лінії регресії Варіант № 3 Знайти вибіркове рівняння прямої лінії регресії X на Y за даними 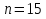 спостережень: спостережень:
Знаходження рівняння лінії регресії. Метод чотирьох полів. Задачі для індивідуальної роботи Обчислити вибірковий коефіцієнт кореляції за даними таблиці Приклад 3.
Приклад 4.
Знайти вибіркове рівняння регресії 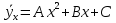 та вибіркове кореляційне відношення та вибіркове кореляційне відношення 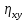 за даними, наведеними в кореляційній таблиці. за даними, наведеними в кореляційній таблиці.Приклад 5.
Приклад 6.
Приклад 7.
Приклад 8.
Приклад 9.
Застосування методів дисперсійного аналізу. Задачі для самостійного розв’язання При рівні значимості 0,05 перевірити нульову гіпотезу про рівність групових середніх. Припускається, що вибірки отримані з нормальних сукупностей з однаковими генеральними дисперсіями. Задача 1.
Відповідь. 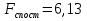 , , 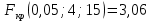 , нульова гіпотеза відхиляється. , нульова гіпотеза відхиляється.Задача 2.
Відповідь. 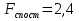 , , 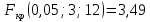 , немає підстав відхилити нульову гіпотезу. , немає підстав відхилити нульову гіпотезу. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

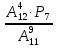
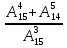
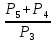
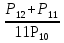
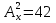
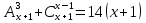
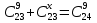
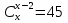
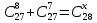
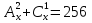
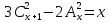
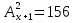
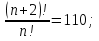 2)
2) 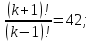
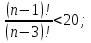 2)
2)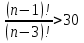
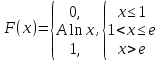 (e/3;e/2)
(e/3;e/2)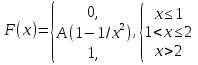 (1,2;1,7))
(1,2;1,7)) 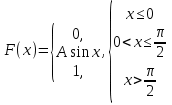 (/4; /3)
(/4; /3)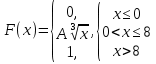 (1;8)
(1;8) 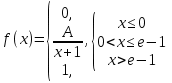 (0;1)
(0;1) 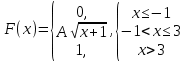 (0;2)
(0;2)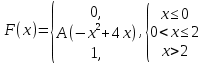 (0;1)
(0;1) 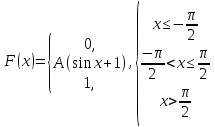 (-/3; /3)
(-/3; /3)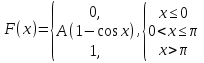 (0; /2)
(0; /2)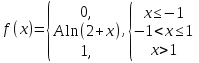 (0;2)
(0;2) 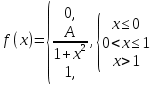 (0;2)
(0;2) 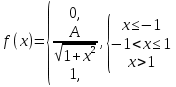 (0;1)
(0;1)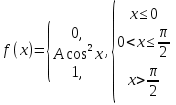 (-/4; /4)
(-/4; /4)