Ответы на билеты по информатики. Основные этапы в информационном развитии общества. Информационные революции
 Скачать 0.77 Mb. Скачать 0.77 Mb.
|
Логические операцииПростейшим и наиболее широко применяемым примером такой алгебраической системы является множество B, состоящее всего из двух элементов: B = { Ложь, Истина } Как правило, в математических выражениях Ложь отождествляется с логическим нулём, а Истина — с логической единицей, а операции отрицания (НЕ), конъюнкции (И) и дизъюнкции (ИЛИ) определяются в привычном нам понимании. Легко показать, что на данном множестве B можно задать четыре унарные и шестнадцать бинарных отношений и все они могут быть получены через суперпозицию трёх выбранных операций. Опираясь на этот математический инструментарий, логика высказываний изучает высказывания и предикаты. Также вводятся дополнительные операции, такие как эквивалентность Логика высказываний послужила основным математическим инструментом при создании компьютеров. Она легко преобразуется в битовую логику: истинность высказывания обозначается одним битом (0 — ЛОЖЬ, 1 — ИСТИНА); тогда операция Впоследствии булева алгебра была обобщена от логики высказываний путём введения характерных для логики высказываний аксиом. Это позволило рассматривать, например, логику кубитов, тройственную логику (когда есть три варианта истинности высказывания: «истина», «ложь» и «не определено») и др. [править]Свойства логических операцийКоммутативность: x Идемпотентность: x Ассоциативность: (x Дистрибутивность конъюнкций и дизъюнкции относительно дизъюнкции, конъюнкции и суммы по модулю два соответственно: Законы де Мо́ргана: Законы поглощения: Другие (1): Другие (2): Другие (3) (Дополнение законов де Мо́ргана): Существуют методы упрощения логической функции: например, Карта Карно, метод Куайна - Мак-Класки Билет №16 основные законы преобразования алгебры логики В алгебре логики имеются законы, которые записываются в виде соотношений. Логические законы позволяют производить равносильные (эквивалентные) преобразования логических выражений. Преобразования называются равносильными, если истинные значения исходной и полученной после преобразования логической функции совпадают при любых значениях входящих в них логических переменных. Для простоты записи приведем основные законы алгебры логики для двух логических переменных А и В. Эти законы распространяются и на другие логические переменные. 1. Закон противоречия: 2. Закон исключенного третьего: 3. Закон двойного отрицания: 4. Законы де Моргана: 5. Законы повторения: A & A = A; A v A = A; В & В = В; В v В = В. 6. Законы поглощения: A ? (A & B) = A; A & (A ? B) = A. 7. Законы исключения констант: A ? 1 = 1; A ? 0 = A; A & 1 = A; A & 0 = 0; B ? 1 = 1; B ? 0 = B; B & 1 = B; B & 0 = 0. 8. Законы склеивания: 9. Закон контрапозиции: (A ? B) = (B ? A). Для логических переменных справедливы и общематематические законы. Для простоты записи приведем общематематические законы для трех логических переменных A, В и С: 1. Коммутативный закон: A & B = B & A; A ? B = B ? A. 2. Ассоциативный закон: A & (B & C) = (A & B) & C; A ? (B ? C) = (A ? B) ? C. 3. Дистрибутивный закон: A & (B ? C) = (A & B) ? (A & C). Как уже отмечалось, с помощью законов алгебры логики можно производить равносильные преобразования логических выражений с целью их упрощения. В алгебре логики на основе принятого соглашения установлены следующие правила (приоритеты) для выполнения логических операций: первыми выполняются операции в скобках, затем в следующем порядке: инверсия (отрицание), конъюнкция ( & ), дизъюнкция (v), импликация (?), эквиваленция (?) Билет №17 построение таблиц истинности, логические законы Порядок выполнения логических операций в сложном логическом выражении: инверсия; конъюнкция; дизъюнкция; импликация; эквивалентность. Для изменения указанного порядка выполнения операций используются скобки. Алгоритм построения таблиц истинности для сложных выражений: Определить количество строк: количество строк = 2n + строка для заголовка, n - количество простых высказываний. Определить количество столбцов: количество столбцов = количество переменных + количество логических операций; определить количество переменных (простых выражений); определить количество логических операций и последовательность их выполнения. Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности с учетом таблиц истинности основных логических операций. Таблица простейших логических функций:
Законы логики и правила преобразования логических выражений В алгебре, которую мы изучаем в школе, существуют пять основных законов: переместительные, сочетательные и распределительный. Среди законов алгебры логики есть подобные законы. 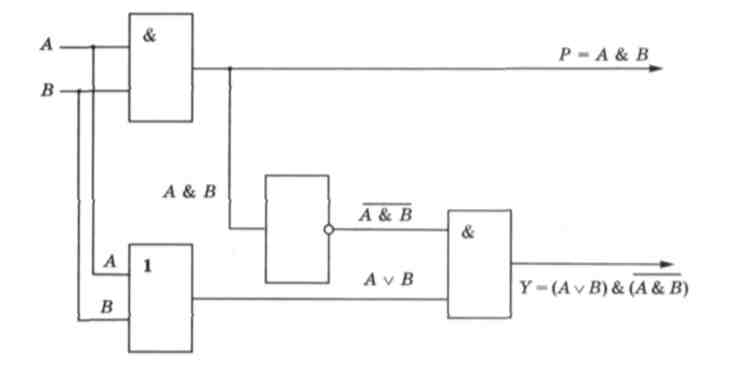 C использованием законов алгебры логики выполняются преобразования сложных логических функций. Если логическая функция представлена с помощью дизъюнкций, конъюнкций и инверсий, то такая форма представления называется нормальной. Логическая функция называется тождественно ложной, если она принимает значение «ложь» на всех наборах входящих в нее простых высказываний. Например: В&¬А&(В А) = В &¬А & (¬В A) = В & ((¬А & ¬В) (¬А & А)) = В & (¬А & ¬В) 0 = (¬А & В &¬ В) = А & 0 = 0. Логическая формула называется тождественно истинной, если она принимает значение «истина» на всех наборах входящих в нее простых высказываний (тождественно истинные высказывания часто называют тавтологиями). Например: ¬ (А&¬А) (В ¬ В) = ¬0 1 = 1. Алгоритм построения таблицы истинности сложного высказывания 1. Вычислить количество строк и столбцов таблицы истинности. Пусть сложное высказывание состоит из n простых. Количество строк: 2n +2 (2-строки заголовка). Количество столбцов: сумма количества переменных (n) + количества логических операций, входящих в сложное высказывание. 2. Начертить таблицу и заполнить заголовок. Первая строка – номера столбцов. Вторая строка - промежуточные формулы и соответствующие им условные записи операций над значениями пар столбцов, содержащие номера этих столбцов. 3. Заполнить первые n столбцов. Для n=3 количество строк со значениями переменных равно 8. 8:2=4: в 1-м столбце чередуем 4 нуля и 4 единицы. 4:2=2: во 2-м столбце чередуем 2 нуля и 2 единицы. 2:2=1: в 3-м столбце чередуем 1 ноль и 1 единицу. Таким образом, все возможные комбинации значений переменных учтены и никакие две не совпадают. 4. Заполнить остальные столбцы. Остальные столбцы заполняем в соответствии с таблицами истинности соответствующих логических операций, причем при заполнении каждого столбца операции выполняются над значениями одного или двух столбцов, расположенных левее заполняемого. Билет №18 решение логических задач методом построения таблиц . Решениелогических задач методом таблиц При решении любой задачи могут быть выделены следующие этапы: 1. Анализ условия задачи ( выделение исходных данных ). 2. Поиск метода решения. 3. Символическая запись задачи. 4. Рассуждения и пояснения к решению. 5. Анализ полученных результатов и запись ответа. При решении задач данного типа я научился представлять исходные данные и рассуждения в виде схем и таблиц, который облегчает процесс решения своей наглядностью. Существует следующая последовательность решения задач с помощью схем: 1. Кратко записать условие, вопрос задачи. Элементы условия задачи отобразить при помощи символьных переменных. 2. Приступить к её решению. - Если по условию между двумя элементами есть соответствие, то они соединяются сплошной линией. - Если же между элементами соответствия нет, то они соединяются пунктирной линией. Чтобы наглядно было видно, какие элементы рассуждений даны, а какие получены по доказательству, можно применять разные цветовые решения ( проводить линии, например, красным (дано) и зелёным (доказательство) карандашами ). А с помощью таблиц решаются задачи с четырьмя, пятью и более парами элементов, когда использование схем неудобно и не наглядно из-за чрезмерной громоздкости. Задача № 1. Подруги Света и Наташа имеют фамилии Иванова и Петрова. Какую фамилию имеет каждая девочка, если Света и Иванова живут в соседних домах? 1. Так как Света не Иванова ( по условию ), значит, Надо: Света - Петрова. Кто какую фамилию имеет? 2. Так как Света - Петрова ( по доказательству ), значит, Наташа не Петрова. 3. Так как Наташа не Петрова ( по доказательству ), значит Наташа Иванова. Ответ: Света имеет фамилию Петрова, а Наташа - Иванова. Билет №19 Хранение информационных объектов различных видов на различных цифровых носителях Информация, закодированная с помощью естественных и формальных языков, а также информация в форме зрительных и звуковых образов хранится в памяти человека. Однако для долговременного хранения информации, ее накопления и передачи из поколе- ния в поколение используются носители информации. Хранение информационных объектов различных видов на различных цифровых носителях Материальная природа носителей информации может быть различной: - молекулы ДНК, которые хранят генетическую информацию; - бумага, на которой хранятся тексты и изображения; - магнитная лента, на которой хранится звуковая информация; - фото- и кинопленки, на которых хранится графическая информация; - микросхемы памяти, магнитные и лазерные диски, на которых хранятся про- граммы и данные в компьютере, и так далее. По оценкам специалистов, объем информации, фиксируемой на различных носите- лях, превышает один эксабайт в год. Примерно 80% всей этой информации хранится в цифровой форме на магнитных и оптических носителях и только 20% - на аналоговых но- сителях (бумага, магнитные ленты, фото- и кинопленки) Большое значение имеет надежность и долговременность хранения информации. Большую устойчивость к возможным повреждениям имеют молекулы ДНК, так как суще- ствует механизм обнаружения повреждений их структуры (мутаций) и самовосстановле- ния. Надежность (устойчивость к повреждениям) достаточно высока у аналоговых но- сителей, повреждение которых приводит к потери информации только на поврежденном участке. Поврежденная часть фотографии не лишает возможности видеть оставшуюся часть, повреждение участка магнитной ленты приводит лишь к временному пропаданию звука и так далее. Цифровые носители гораздо более чувствительны к повреждениям, даже утеря од- ного бита данных на магнитном или оптическом диске может привести к невозможности считать файл, то есть к потере большого объема данных. Именно поэтому необходимо со- блюдать правила эксплуатации и хранения цифровых носителей информации. Наиболее долговременным носителем информации является молекула ДНК, кото- рая в течение десятков тысяч лет (человек) и миллионов лет (некоторые живые организ- мы), сохраняет генетическую информацию данного вида . Аналоговые носители способны сохранять информацию в течение тысяч лет (еги- петские папирусы и шумерские глиняные таблички), сотен лет (бумага) и десятков лет (магнитные ленты, фото- и кинопленки). Цифровые носители появились сравнительно недавно и поэтому об их долговре- менности можно судить только по оценкам специалистов. По экспертным оценкам, при правильном хранении оптические носители способны хранить информацию сотни лет, а магнитные - десятки лет. Билет №20 поиск информации с использованием компьютера Билет №21 передача информации между компьютерами Передача информации между компьютерами существует с самого момента возникновения ЭВМ. Она позволяет организовать совместную работу отдельных компьютеров, решать одну задачу с помощью нескольких компьютеров, совместно использовать ресурсы и решать множество других проблем. Под компьютерной сетью понимают систему распределенных на территории аппаратных, программных и информационных ресурсов (средств ввода/вывода, хранения и обработки информации), связанных между собой каналами передачи данных. При этом обеспечивается совместный доступ пользователей к информации (базам данных, документам и т.д.) и ресурсам (жесткие диски, принтеры, накопители CD-ROM, модемы, выход в глобальную сеть и т.д.). По типу используемых ЭВМ выделяют однородные и неоднородные сети. В неоднородных сетях содержатся программно несовместимые компьютеры (чаще так и бывает на практике). По территориальному признаку сети делят на локальные, региональные и глобальные. Локальные сети (LAN, Local Area Network) охватывают ресурсы, расположенные друг от друга не более чем на несколько километров (чаще всего это одно-два здания и прилегающая к ним территория - например, локальная сеть школы, вуза, компьютерного клуба и т.д.). Региональные сети охватывают город, район, область, небольшую республику (например, сеть Департамента образования Пермской области). Глобальные сети охватывают всю страну, несколько стран и целые континенты (например, сеть Интернет). Иногда выделяют корпоративные сети, где важно защитить информацию от несанкционированного доступа (например, сеть Министерства обороны). По методу передачи информации различают сети с коммутацией каналов, сообщений, пакетов и со смешанной коммутацией. Чаще используются сети с коммутацией пакетов. В зависимости от того, являются ли все компьютеры локальной сети равноправными или имеется выделенный центральный компьютер (сервер), сети подразделяют на одноранговые, или сети с выделенным сервером. Сеть с выделенным сервером является более производительной. Вообще сервером называется узел сети, который предоставляет свои ресурсы другим узлам (компьютерам и т.д.), но сам при этом не использует их ресурсы. Клиентом называется узел сети, который только использует сетевые ресурсы, но сам свои ресурсы в сеть не отдает (часто его еще называют рабочей станцией). Основными свойствами локальной сети являются: высокая скорость передачи, большая пропускная способность; низкий уровень ошибок передачи; эффективный, быстродействующий механизм управления обменом; ограниченное, точно определенное число компьютеров, подключаемых к сети. Очень важным является вопрос топологии локальной сети. Под топологией компьютерной сети обычно понимают физическое расположение компьютеров сети относительно Друг Друга и способ соединения их линиями. Топология определяет требования к оборудованию, тип используемого кабеля, методы управления обменом, надежность работы, возможность расширения сети. Существует три основных топологии сети. Шина (bus), при которой все компьютеры параллельно подключаются к одной линии связи, и информация от каждого компьютера одновременно передается ко всем остальным компьютерам.  Согласно этой топологии создается одно-ранговая сеть. При таком соединении компьютеры могут передавать информацию только по очереди, так как линия связи единственная. Достоинства: простота добавления новых узлов в сеть (это возможно даже во время работы сети); сеть продолжает функционировать, даже если отдельные компьютеры вышли из строя; недорогое сетевое оборудование за счет широкого распространения такой топологии. Недостатки: сложность сетевого оборудования; сложность диагностики неисправности сетевого оборудования из-за того, что все адаптеры включены параллельно; обрыв кабеля влечет за собой выход из строя всей сети; ограничение на максимальную длину линий связи из-за того, что сигналы при передаче ослабляются и никак не восстанавливаются. 2. Звезда (star), при которой к одному центральному компьютеру присоединяются остальные периферийные компьютеры, причем каждый из них использует свою отдельную линию связи. 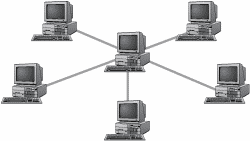 Весь обмен информацией идет исключительно через центральный компьютер, на который ложится очень большая нагрузка, поэтому он предназначен только для обслуживания сети. Достоинства: выход из строя периферийного компьютера никак не отражается на функционировании оставшейся части сети; простота используемого сетевого оборудования; все точки подключения собраны в одном месте, что позволяет легко контролировать работу сети, локализовать неисправности сети путем отключения от центра тех или иных периферийных устройств; не происходит затухания сигналов. Недостатки: выход из строя центрального компьютера делает сеть полностью неработоспособной; жесткое ограничение количества периферийных компьютеров; значительный расход кабеля. 2. Кольцо (ring), при котором каждый компьютер передает информацию всегда только одному компьютеру, следующему в цепочке, а получает информацию только от предыдущего в цепочке компьютера, и эта цепочка замкнута. Особенностью кольца является то, что каждый компьютер восстанавливает приходящий к нему сигнал, поэтому затухание сигнала во всем кольце не имеет никакого значения, важно только затухание между соседними компьютерами.  Достоинства: Достоинства: легко подключить новые узлы, хотя для этого нужно приостановить работу сети; большое количество узлов, которое можно подключить к сети (более 1000); высокая устойчивость к перегрузкам. Недостатки: выход из строя хотя бы одного компьютера нарушает работу сети; обрыв кабеля хотя бы в одном месте нарушает работу сети. В отдельных случаях при конструировании сети используют комбинированную топологию. Например, дерево (tree) - комбинация нескольких звезд. Каждый компьютер, который функционирует в локальной сети, должен иметь сетевой адаптер (сетевую карту). Функцией сетевого адаптера является передача и прием сигналов, распространяемых по кабелям связи. Кроме того, компьютер должен быть оснащен сетевой операционной системой. При конструировании сетей используют следующие виды кабелей: неэкранированная витая пара. Максимальное расстояние, на котором могут быть расположены компьютеры, соединенные этим кабелем, достигает 300 м. Скорость передачи информации - от 10 до 155 Мбит/с; экранированная витая пара. Скорость передачи информации - 16 Мбит/с на расстояние до 90 м. Обладает лучшей по сравнению с неэкранированной витой парой помехозащищенностью; коаксиальный кабель. Позволяет передавать информацию на расстояние до 2000 м со скоростью 2-44 Мбит/с; волоконно-оптический кабель. Позволяет передавать информацию на расстояние до 10 000 м со скоростью до 10 Гбит/с. Теперь поговорим о глобальных сетях. На сегодняшний день их насчитывается в мире более 200. Из них наиболее известной и самой популярной является сеть Интернет. В отличие от локальных сетей в глобальных сетях нет какого-либо единого центра управления. Основу сети составляют десятки и сотни тысяч компьютеров, соединенных теми или иными каналами связи. Каждый компьютер имеет уникальный идентификатор, что позволяет "проложить к нему маршрут" для доставки информации. Обычно в глобальной сети объединяются компьютеры, работающие по разным правилам (имеющие различную архитектуру, системное программное обеспечение и т.д.). Поэтому для передачи информации из одного вида сетей в другой используются шлюзы (gateway) - устройства (компьютеры), служащие для объединения сетей с совершенно различными протоколами обмена. Протокол обмена - это набор правил (соглашение, стандарт) передачи информации в сети. Протоколы условно делятся на базовые (более низкого уровня), отвечающие за передачу информации любого типа, и прикладные (более высокого уровня), отвечающие за функционирование специализированных служб. Для работы в глобальной сети пользователю необходимо иметь соответствующее аппаратное и программное обеспечение. Программное обеспечение можно разделить на два класса: программы-серверы, которые размещаются на узле сети, обслуживающем компьютер пользователя; программы-клиенты, размещенные на компьютере пользователя и пользующиеся услугами сервера. Глобальные сети предоставляют пользователям разнообразные услуги Подключение к глобальной сети может осуществляться одним из способов: удаленный доступ по коммутируемой телефонной линии. В этом случае в распоряжении пользователя должны быть модем, который преобразует подаваемую на него компьютером цифровую информацию в аналоговый сигнал (модуляция), и телефон. Аналоговый сигнал передается по телефонной линии, а модем на принимающей стороне совершает обратное преобразование информации (демодуляцию). Скорость, с которой будет производиться обмен информацией, определяется прежде всего скоростью передачи модема пользователя и качеством телефонной линии. Для предупреждения искажения информации в процессе ее передачи и приема модем обычно работает в режиме коррекции ошибок, когда информация передается маленькими порциями, вычисляется контрольная сумма, которая также передается. Если отмечается искажение какой-то порции информации, ее передача повторяется; прямой доступ по выделенному каналу. Данный способ дороже, чаще его используют те или иные организации. В качестве выделенных каналов могут использоваться коаксиальные и оптоволоконные кабели, радиорелейные линии, спутниковая связь. Билет №22 управление процессами | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
