|
|
вопросы физика. Основные характеристики теплового излучения
Спектр излучения атома водорода.
Энергия атома как микроскопической системы принимает дискретный ряд значений (квантуется) соответствующих стационарным состояниям атома. В частности, подтверждением этого является анализ огромного экспериментального материала, накопленного при изучении атомных спектров излучения и поглощения.
Спектр излучения атомов – это набор узких, почти монохроматических максимумов интенсивности излучения при некоторых длинах волн, называемых спектральными линиями. Спектральные линии возникают вследствие перехода электронов в атомах с одного энергетического уровня на другой. Переход этот происходит за время
10-8 с. По мере удаления от ядра энергия электрона увеличивается. При переходе в атоме с более высокого энергетического уровня на более низкий электрон излучает квант энергии 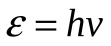 . В процессе такого перехода изменяется величина главного квантового числа. Величину энергии кванта излучения рассчитывают на основании теории Шредингера по уравнению (5.53). . В процессе такого перехода изменяется величина главного квантового числа. Величину энергии кванта излучения рассчитывают на основании теории Шредингера по уравнению (5.53).
Пусть электрон находится вначале на энергетическом уровне с энергией Emопределяемой главным квантовый числом m. Затем он перешел на уровень с энергией Еnи главным квантовым числом n. Энергия кванта излучения равна разности энергий Еmи Еn:
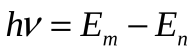 (5.61) (5.61)
Частота излучения с учетом зависимостей (5.53) и (5.61)
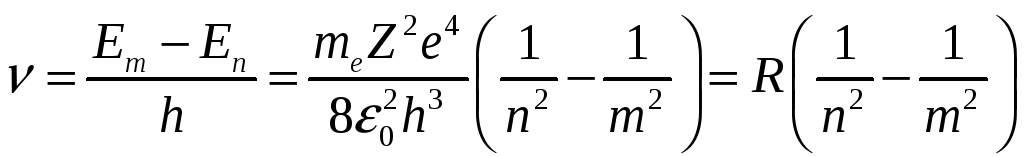 (5.62), (5.62),
где 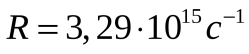 - постоянная Ридберга. Соотношение (5.62) называется обобщенной формулой Бальмера. - постоянная Ридберга. Соотношение (5.62) называется обобщенной формулой Бальмера.
Впервые подобную формулу, описывающую все известные в то время спектральные линии атома водорода в видимой области спектра (для 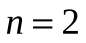 и и 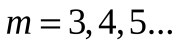 ) получил экспериментально швейцарский ученый Бальмер: ) получил экспериментально швейцарский ученый Бальмер: 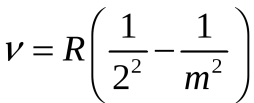 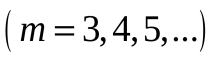 (5.63) (5.63)
Спектральные линии, отличающиеся различными значениями 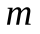 , образуют группу или серию линий и при , образуют группу или серию линий и при 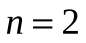 серия называется серией Бальмера. С увеличением серия называется серией Бальмера. С увеличением 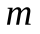 линии серии сближаются, значение линии серии сближаются, значение 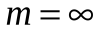 определяет границу серии, к которой со стороны больших частот примыкает сплошной спектр. определяет границу серии, к которой со стороны больших частот примыкает сплошной спектр.
В начале 20 века в спектре атома водорода было обнаружено ещё несколько серий. В ультрафиолетовой области спектра (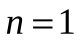 ) находится серия Лаймана: ) находится серия Лаймана:
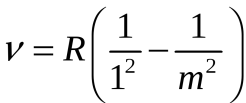 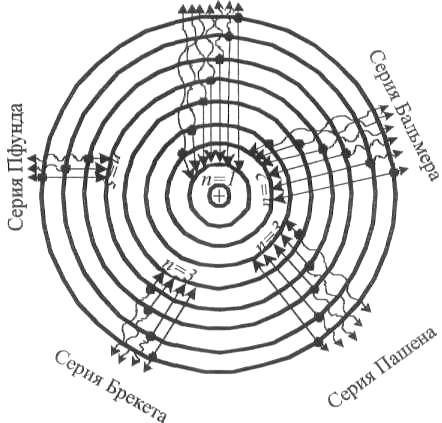 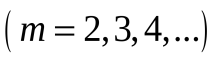
В инфракрасной области спектра находятся:
серия Пашена 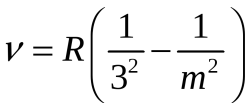 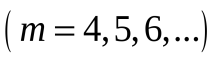
серия Брэкета 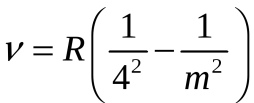 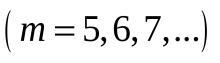
серия Пфунда 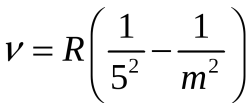 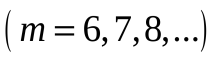
серия Хэмфри 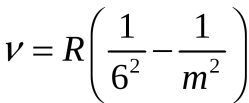 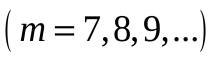
Т.о. спектральные серии – группа спектральных линий, возникающих при переходе электронов в атомах с различных энергетических уровней на один и тот же уровень (см. рис.).
18. Модель атома по Томпсону

19. Модель атома Резерфорда

20. Модель атома Бора

21. Опыты Франка и Герца
Эксперимент Франка и Герца является прямым подтверждением постулатов Бора о том, что:
Атом и атомные системы могут длительно пребывать в определенных стационарных состояниях, в которых, не смотря на происходящие в них движения заряженных частиц, они не излучает и не поглощает энергию. Каждому состоянию соответствует свое дискретное значение энергии.
Изменение внутренней энергии атома может происходить лишь при переходе между состояниями и равно разности энергий этих состояний (энергии перехода).
22. Теория Бора—Зоммерфельда
 
23. Волны Луи де Бройля
Волны де Бройля– волны, связанные с любой движущейся материальной частицей. Любая движущаяся частица (например, электрон) ведёт себя не только как локализованный в пространстве перемещающийся объект - корпускула, но и как волна, причём длина этой волны даётся формулой λ = h/р, где h = 6.6·10-34 Дж.сек – постоянная Планка, а р – импульс частицы. Эта волна и получила название волны де Бройля (в честь французского физика-теоретика Луи де Бройля, впервые высказавшего гипотезу о таких волнах в 1923 г.). Если частица имеет массу m и скорость v << с (с – скорость света), то импульс частицы р = mv и дебройлевская длина волны связаны соотношением λ = h/mv.
Волновые свойства макроскопических объектов не проявляются из-за малых длин волн. Так для тела массой 200 г, движущегося со скоростью 3 м/сек, длина волны ≈10-31 см, что лежит далеко за пределами наблюдательных возможностей. Однако для микрочастиц длины волн лежат в доступной наблюдению области. Например, для электрона, ускоренного разностью потенциалов 100 вольт, длина волны ≈10-8 см, что соответствует размеру атома.
Для расчёта длины волны де Бройля частицы массы m, имеющей кинетическую энергию E, удобно использовать соотношение
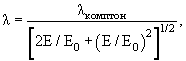
где E0 = mc2 − энергия покоя частицы массы m,
λкомптон = h/mc − комптоновская длина волны частицы,
λкомптон (электрон) = 2.4·10-12 м = 0.024 Å,
λкомптон (протон) = 1.32·10-15 м = 1.32 фм.
Длина волны де Бройля фотона с энергией Е определяется из соотношения
λ(фм) = h/p = hc/E = 2π·197 МэВ·фм /E(МэВ).
Существование волн де Бройля доказано многочисленными экспериментами, в которых частицы ведут себя как волны. Так при рассеянии пучка электронов с энергией 100 эВ на упорядоченной системе атомов кристалла, играющего роль дифракционной решётки, наблюдается отчётливая дифракционная картина. Существование волн де Бройля лежит в основе работы электронного микроскопа, разрешающая способность которого намного порядков выше, чем у любого оптического микроскопа, что позволяет наблюдать молекулы и атомы, а также в основе методов исследования таких сверхмалых объектов, как атомные ядра и элементарные частицы, бомбардировкой их частицами высоких энергий. Метод дифракции частиц в настоящее время широко используется при изучении строения и свойств вещества
24. Соотношение неопределенностей
 
25. Волновая функция

26. Уравнение Шрёдингера

27. Столкновение квантовой частицы с потенциальным барьером
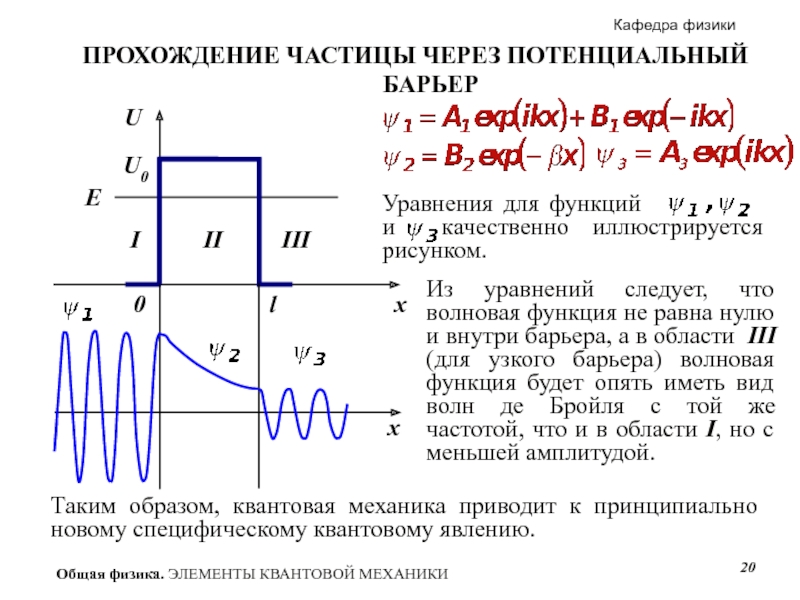
28. Туннельный эффект

29. Постулаты квантовой механики
К числу основополагающих идей квантовой теории, рассмотренных в первой главе, относятся:
1) идея квантования (дискретность), согласно которой физические величины, относящиеся к микрообъектам (квантовым системам), могут принимать в соответствующих условиях только вполне определённые, т.е. дискретные значения;
2) идея корпускулярно-волнового дуализма, утверждающая, что с каждым микрообъектом уравнениями де Бройля связываются, с одной стороны, корпускулярные характеристики (энергия Е и вектор импульса 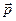 ) и, с другой стороны, волновые характеристики (частота ω и волновой вектор ) и, с другой стороны, волновые характеристики (частота ω и волновой вектор 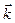 ); );
3) идея статистического характера основных закономерностей в природе, в связи с чем квантовая механика предсказывает (позволяет рассчитывать) вероятности измерения дозволенных значений физических величин.
В квантовой механике решаются три типа практических задач. Задача первого типа (прямая): зная состояние квантовой системы, требуется предсказать возможные результаты измерений её физических величин. Задача второго типа (обратная): по результатам эксперимента определить состояние квантовой системы. В задачах третьего типа изучается изменение состояния квантовой системы со временем. Эти задачи связаны с представлениями о квантовом статистическом ансамбле и роли и свойствах измерительных приборов.
Для построения логически стройной теории, решения указанных задач и многих других вопросов в основу квантовой механики положены следующие принципы и постулаты:
1. Принцип соответствия.
2. Определение состояния квантовой системы.
3. Принцип суперпозиции.
4.Постулат квантования.
5. Постулат вероятности.
6. Принцип тождественности одинаковых частиц и постулат симметрии.
Реклама
30. Частица в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками»
Свободная частица — частица, движущаяся в отсутствие внешних полей. Так как на свободную частицу (пусть она движется вдоль оси х) силы не действуют, то потенциальная энергия частицы U (х) = соnstи ее можно принять равной нулю. Тогда полная энергия частицы совпадает с ее кинетической энергией. Энергия свободной частицы может принимать любые значения, т. е. ее энергетический спектр является непрерывным. Свободная квантовая частица описывается плоской монохроматической волной де Бройля, и все положения свободной частицы в пространстве являются равновероятными.
П роведем качественный анализ решений уравнения Шредингера применительно к свободной частице в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками» (рис.33.1). Такая «яма» описывается потенциальной энергией вида (для простоты принимаем, что частица движется вдоль оси х) роведем качественный анализ решений уравнения Шредингера применительно к свободной частице в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками» (рис.33.1). Такая «яма» описывается потенциальной энергией вида (для простоты принимаем, что частица движется вдоль оси х)
∞, х < 0
U(x) ={0, 0 ≤ х ≤ l(33.11)
∞, х > 1
где l — ширина «ямы», а энергия отсчитывается от ее дна (рис.33.1).
Уравнение Шредингера для стационарных состояний в случае одномерной задачи запишется в виде
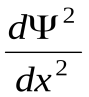 + + 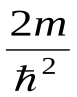 (Е- U)Ψ =0. (33.12) (Е- U)Ψ =0. (33.12)
По условию задачи (бесконечно высокие «стенки»), частица не проникает за пределы «ямы», поэтому вероятность ее обнаружения (а следовательно, и волновая функция) за пределами «ямы» равна нулю. На границах «ямы» (при х=0 и х=l) непрерывная волновая функция также должна обращаться в нуль. Следовательно, граничные условия в данном случае имеют вид
Ψ(0)=Ψ(l)=0. (33.13)
В пределах «ямы» уравнение Шредингера сведется к уравнению
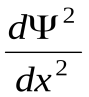 + + 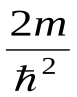 ЕΨ =0. (33.14) ЕΨ =0. (33.14)
Стационарное уравнение Шредингера, описывающее движение частицы в «потенциальной яме» с бесконечно высокими «стенками», удовлетворяется только при собственных значениях Еп зависящих от целого числа п.
Еп= 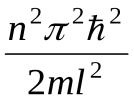 ,( n= 1, 2, 3, …).(33.15) ,( n= 1, 2, 3, …).(33.15)
Следовательно, энергия Еп частицы в «потенциальной яме» с бесконечно высокими «стенками» принимает лишь определенные дискретные значения, т.е. квантуется. Квантованные значения энергии Еп - называются уровнями энергии, а число п, определяющее энергетические уровни частицы, называется главным квантовым числом. Таким образом, микрочастица в «потенциальной яме» с бесконечно высокими «стенками» может находиться только на определенном энергетическом уровне Еп, или, как говорят, частица находится в квантовом состоянии п. Частица «в потенциальной яме» с бесконечно высокими «стенками» не может иметь энергию меньшую, чем минимальная энергия, равная 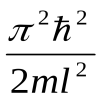 . .
31. Квантовая частица в непроницаемой сфере
32. Квантовая частица в потенциальном ящике с непроницаемыми стенками
33. Квантовый осциллятор
Линейным гармоническим осциллятором в классической механике называется система, совершающая колебательное периодическое движение под действием квазиупругой силы около положения устойчивого равновесия, описываемое уравнением вида . Данная система является моделью, используемой при описании классических и квантовых систем. Пружинный, физический и математический маятники – примеры классических гармонических осцилляторов.
Согласно классической механике одномерный осциллятор совершает гармонические колебания с циклической частотой 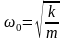 , где k – постоянная квазиупругой силы. Поэтому потенциальная энергия одномерного гармонического осциллятора может быть определена как парабола , где k – постоянная квазиупругой силы. Поэтому потенциальная энергия одномерного гармонического осциллятора может быть определена как парабола 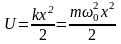 . .
Классический осциллятор не может выйти за пределы потенциальной «ямы» с координатами 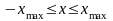 , где , где 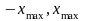 – координаты точек поворота, в которых E=U . Частица может двигаться только в области, где – координаты точек поворота, в которых E=U . Частица может двигаться только в области, где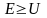 , т. е. между точками поворота. В квантовой теории задача о квантовом гармоническом осцилляторе сводится к задаче о движении частицы массой m в параболической потенциальной яме. Уравнение Шрёдингера для одномерного квантового осциллятора, для которого потенциальная энергия имеет вид, записывается так: , т. е. между точками поворота. В квантовой теории задача о квантовом гармоническом осцилляторе сводится к задаче о движении частицы массой m в параболической потенциальной яме. Уравнение Шрёдингера для одномерного квантового осциллятора, для которого потенциальная энергия имеет вид, записывается так: 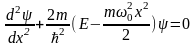 , где Е – полная энергия осциллятора. В уравнении , где Е – полная энергия осциллятора. В уравнении 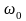 имеет смысл циклической частоты классического одномерного осциллятора. Собственные значения энергии для этого уравнения, как можно доказать, равны имеет смысл циклической частоты классического одномерного осциллятора. Собственные значения энергии для этого уравнения, как можно доказать, равны 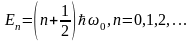
Таким образом, энергия квантового осциллятора в отличие от классического не может быть произвольной, а квантуется (может иметь лишь дискретные значения). Разность энергии между соседними уровнями определяется как дельта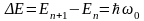 . .
Следовательно, уровни энергии квантового осциллятора расположены через равные интервалы 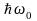 и называются эквидистантными. и называются эквидистантными.
Минимальная энергия квантового осциллятора лежит выше минимума потенциальной энергии U = 0 . Неравенство нулю 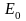 осциллятора – типично квантовый эффект – прямое следствие соотношения неопределенностей. Наличие нулевой энергии подтверждается экспериментально. осциллятора – типично квантовый эффект – прямое следствие соотношения неопределенностей. Наличие нулевой энергии подтверждается экспериментально.
Следовательно, энергия гармонического осциллятора в излучательных процессах может изменяться только порциями : гармонический осциллятор испускает и поглощает энергию квантами.
Решения уравнения таковы, что имеется отличная от нуля вероятность обнаружить частицу за пределами области , т. е. в классически запрещенной области, где E за пределами потенциальной «ямы» объясняется волновыми свойствами микрочастиц.
Отметим, что рассмотренная модель гармонического осциллятора и связанная с ним задача о движении частицы в параболической потенциальной «яме» является идеализацией, которая справедлива только при малых отклонениях колеблющейся частицы от положения равновесия. В реальных системах потенциальная энергия U частицы, совершающей колебания около положения равновесия, имеет более сложный вид. При возрастании амплитуды колебаний движение частицы будет все больше усложняться, отличаясь от гармонических колебаний. Такое движение называют ангармоническим движением, а соответствующий осциллятор – ангармоническим осциллятором.
34. Квантовый ротатор
Рассмотрим сначала случай одномерного жесткого ротатора, под которым понимают частицу массой m, движущуюся по окружности радиуса R. Если m и R имеют порядок атомных, одномерный ротатор называется квантовым. Потенциальная энергия U, удерживающая частицу на окружности, постоянна; ее удобно положить равной нулю. Удобно перейти также к полярной системе координат R, 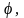 где где 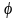 – угол, образуемый радиус-вектором R с осью X. Уравнение Шредингера в этом случае будет иметь вид – угол, образуемый радиус-вектором R с осью X. Уравнение Шредингера в этом случае будет иметь вид
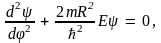
или
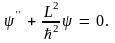 (10.16) (10.16)
Здесь 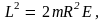 откуда откуда
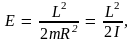
где 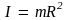 – момент инерции частицы. – момент инерции частицы.
Решение уравнения (10.16) можно записать в виде
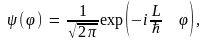 (10.17) (10.17)
где коэффициент 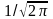 получен из условия нормировки получен из условия нормировки 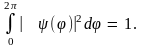 Условие однозначности функции (10.17) требует, чтобы при изменении угла Условие однозначности функции (10.17) требует, чтобы при изменении угла 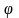 на на 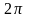 она принимала бы свое прежнее значение, т.е. должно выполняться равенство она принимала бы свое прежнее значение, т.е. должно выполняться равенство
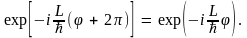
Это так называемое периодическое (или, как говорят, циклическое) граничное условие приводит к равенству
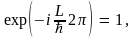
откуда получаем
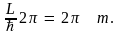
Здесь 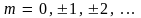 – любое целое число. Откуда – любое целое число. Откуда
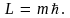
Следовательно, что момент импульса одномерного ротатора принимает лишь дискретные значения, кратные постоянной 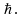 Эта постоянная, таким образом, является элементарным квантом действия. Квантуется и энергия одномерного ротатора: Эта постоянная, таким образом, является элементарным квантом действия. Квантуется и энергия одномерного ротатора:
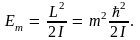
В случае трехмерного квантового ротатора – микрочастицы, движущейся по поверхности сферы радиуса R, квантуется момент импульса частицы:
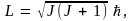
где 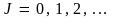 – так называемое азимутальное, или вращательное квантовое число. Поскольку J – постоянная величина для любого квантового состояния, то и момент импульса является постоянным. Так и должно быть, так как закон сохранения момента импульса справедлив и в квантовой механике, как и в классической. Сила, действующая на частицу, направлена к силовому центру, действие которого и заставляет частицу двигаться по поверхности шара, т.е. противоположны направлению радиус-вектора R. Поэтому момент силы, действующий на ротатор со стороны силового центра, – так называемое азимутальное, или вращательное квантовое число. Поскольку J – постоянная величина для любого квантового состояния, то и момент импульса является постоянным. Так и должно быть, так как закон сохранения момента импульса справедлив и в квантовой механике, как и в классической. Сила, действующая на частицу, направлена к силовому центру, действие которого и заставляет частицу двигаться по поверхности шара, т.е. противоположны направлению радиус-вектора R. Поэтому момент силы, действующий на ротатор со стороны силового центра, 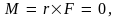 откуда и следует, что L = const. откуда и следует, что L = const.
Квантуется также проекция момента импульса на произвольное z-направление в пространстве,
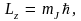
где 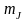 – квантовое число, определяющее проекцию момента импульса частицы. Из условия – квантовое число, определяющее проекцию момента импульса частицы. Из условия 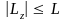 получаем квантовое что получаем квантовое что 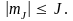 Следовательно, квантовое число может принимать все значения от –J до J – всего 2J + 1 значений. Дискретность допустимых значений квантового числа означает, что возможны только некоторые направления момента импульса (рис. 10.). Данные рисунка соответствуют значению l = 2; радиус полуокружности равен (в принятом масштабе) L, т.е. Следовательно, квантовое число может принимать все значения от –J до J – всего 2J + 1 значений. Дискретность допустимых значений квантового числа означает, что возможны только некоторые направления момента импульса (рис. 10.). Данные рисунка соответствуют значению l = 2; радиус полуокружности равен (в принятом масштабе) L, т.е. 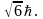 Это обстоятельство называется пространственным квантованием. Это обстоятельство называется пространственным квантованием.
Энергия трехмерного ротатора принимает значения, равные
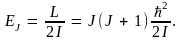 (10.18) (10.18)
Как видим, квантуется и полная энергия ротатора. В основном состоянии, т.е. при J = 0, имеем E0 = 0 – нулевая энергия у ротатора отсутствует.
Расстояние между соседними уровнями энергии ротатора
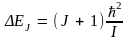
Увеличивается с ростом номера уровня (квантового числа J), так
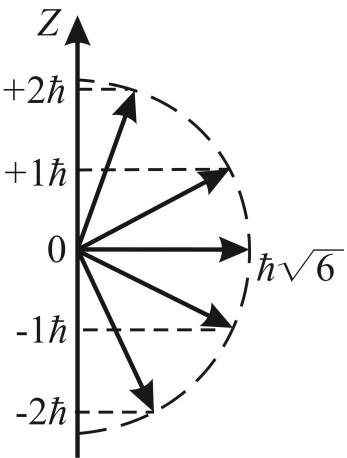
Рис. 10.
| что уровни энергии ротатора не эквидистантны. Относительное расстояние между энергетическими уровнями
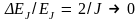
при 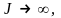 т.е. спектр энергии становится непрерывным (движение ротатора принципу соответствия Бора удовлетворяет). В классическом приближении, когда т.е. спектр энергии становится непрерывным (движение ротатора принципу соответствия Бора удовлетворяет). В классическом приближении, когда 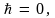 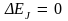 – квантование энергии исчезает – спектр энергии будет непрерывным. Заметим, что в любом состоянии (J = const) сохраняется и энергия ротатора. – квантование энергии исчезает – спектр энергии будет непрерывным. Заметим, что в любом состоянии (J = const) сохраняется и энергия ротатора.
Волновая функция пространственного ротатора определяется двумя квантовыми числами J и mJ: 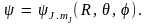 Эти квантовые числа и определяют квантовое состояние ротатора. Поскольку при этом энергия ротатора определяется только одним квантовым числом J, то все уровни энергии, кроме основного (J = = 0), вырождены. Кратность вырождения определяется числом значений mJ, возможных при заданном J, и равна wJ = 2J + 1. Столько существует собственных функций Эти квантовые числа и определяют квантовое состояние ротатора. Поскольку при этом энергия ротатора определяется только одним квантовым числом J, то все уровни энергии, кроме основного (J = = 0), вырождены. Кратность вырождения определяется числом значений mJ, возможных при заданном J, и равна wJ = 2J + 1. Столько существует собственных функций 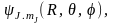 соответствующих одному и тому же значению энергии EJ. соответствующих одному и тому же значению энергии EJ.
35. Атом водорода в квантовой механике
Атом водорода — физическая система, состоящая из атомного ядра, несущего элементарный положительный электрический заряд, и электрона, несущего элементарный отрицательный электрический заряд. В состав атомного ядра может входить протон или протон с одним или несколькими нейтронами, образуя изотопы водорода. Электрон преимущественно находится в тонком концентрическом шаровом слое вокруг атомного ядра, образуя электронную оболочку атома. Наиболее вероятный радиус электронной оболочки атома водорода в стабильном состоянии равен боровскому радиусу a0 = 0,529 Å.
Квантовые числа.
Квантовые числа – энергетические параметры, определяющие состояние электрона и тип атомной орбитали, на которой он находится.
Главное квантовое число n определяет общую энергию электрона и степень его удаления от ядра.
Орбитальное квантовое число L определяет форму атомной орбитали.
Магнитная квантовое число m определяет ориентацию орбитали в пространстве относительно внешнего магнитного или электрического поля.
Спектральные серии водорода.
Спектральные серии водорода – набор спектральных серий, составляющих спектр атома водорода. Поскольку водород – наиболее простейший атом, его спектральные серии наиболее изучены. Они очень хорошо подчиняются формуле Ридберга.
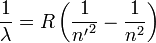
Где R = 109 677 см-1 – постоянная Ридберга для водорода, n’ – основной уровень серии.
Спектральные линии, возникающие при переходах на основной энергетический уровень, называются резонансными, все остальные – субординатными.
Серия Лаймана – все линии находятся в ультрафиолетовом диапазоне.Серия соответствует формуле Ридберга при n’ =1 и n = 2, 3, 4, …;
Серия Бальмера – первые четыре линии серии находятся в видимом диапазоне. Серия соответствует формуле Ридберга при n’ = 2 и n = 3, 4, 5 …;
Серия Пашена – все линии находятся в инфракрасном диапазоне. Серия соответствует формуле Ридберга при n’ =3 и n = 4, 5, 6, …;
Серия Пфунда – линии серии находятся в ближнем инфракрасном диапазоне. Серия соответствует формуле Ридберга при n’ = 5 и n = 6, 7, 8, …;
|
|
|
 Скачать 2.41 Mb.
Скачать 2.41 Mb.







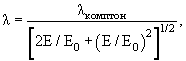






 роведем качественный анализ решений уравнения Шредингера применительно к свободной частице в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками» (рис.33.1). Такая «яма» описывается потенциальной энергией вида (для
роведем качественный анализ решений уравнения Шредингера применительно к свободной частице в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками» (рис.33.1). Такая «яма» описывается потенциальной энергией вида (для