При расчетах цепей синусоидального тока используют символический метод расчета или метод комплексных амплитуд. В этом методе сложение двух синусоидальных токов заменяют сложением двух комплексных чисел, соответствующих этим токам.
Из курса математики известно, что комплексное число может быть записано в показательной или алгебраической форме:
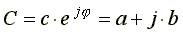
где с - модуль комплексного числа;
φ- аргумент;
a - вещественная часть комплексного числа;
b - мнимая часть;
j - мнимая единица, j = √-1.
С помощью формулы Эйлера можно перейти от показательной формы записи к алгебраической.
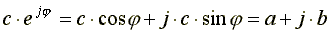
От алгебраической формы записи переходят к показательной форме с помощью формул:
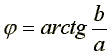
Комплексное число может быть представлено в виде радиус - вектора в комплексной плоскости. Вектор длиной, равной модулю c, расположен в начальный момент времени под углом φ относительно вещественной оси (рис.6.3).
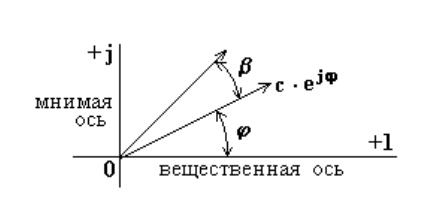
Рис.6.3
Умножим комплексное число на множитель .
Радиус - вектор на комплексной плоскости повернется на угол β.
Множитель называется поворотным.
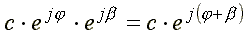
Если , то вектор, умноженный на , превратится во вращающийся со скоростью ω радиус - вектор.
Выражение 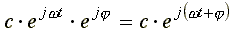 называется комплексной функцией времени. называется комплексной функцией времени.
Применительно к напряжению, получим 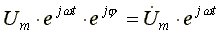 - комплексную функцию времени для напряжения. - комплексную функцию времени для напряжения.
- комплексная амплитуда напряжения (исходное положение вектора в комплексной плоскости). Определим, чему равна мнимая часть комплексной функции времени для напряжения.
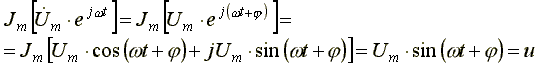
Мгновенное синусоидальное напряжение (ток, ЭДС) является мнимой частью соответствующей комплексной функции времени.
Замечание. В электротехнике над символами, изображающими комплексные напряжения, токи, ЭДС, принято ставить точку.
Синусоидальные функции времени могут быть представлены векторами в комплексной плоскости, вращающимися против часовой стрелки с постоянной угловой скоростью ω. Проекция вектора на мнимую ось изменяется по синусоидальному закону.
Пример.
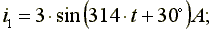 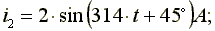
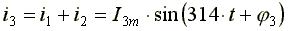
Сложение синусоидальных токов заменим сложением комплексных амплитуд, соответствующих этим токам.
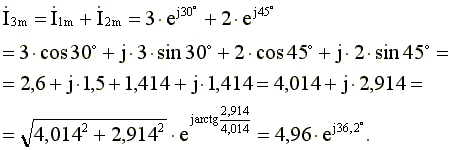
Амплитуда результирующего тока , начальная фаза - .
Мгновенное значение результирующего тока
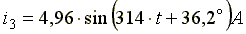 . .
Законы Ома и Кирхгофа в комплексной форме:
- закон Ома; (6.4)
- первый закон Кирхгофа; (6.5)
- второй закон Кирхгофа. (6.6)
6.4. Сопротивление в цепи синусоидального тока
Если напряжение 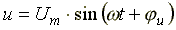 подключить к сопротивлению R, то через него протекает ток подключить к сопротивлению R, то через него протекает ток
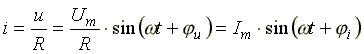 (6.7) (6.7)
Анализ выражения (6.7) показывает, что напряжение на сопротивлении и ток, протекающий через него, совпадают по фазе.
Формула (6.7) в комплексной форме записи имеет вид
(6.8)
где и - комплексные амплитуды тока и напряжения.
Комплексному уравнению (6.8) соответствует векторная диаграмма (рис. 6.4).
Из анализа диаграммы следует, что векторы напряжения и тока совпадают по направлению.
Сопротивление участка цепи постоянному току называется омическим, а сопротивление того же участка переменному току - активным сопротивлением.
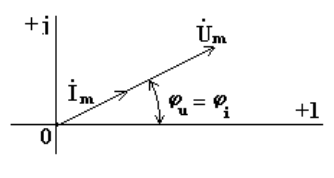
Рис.6.4
Активное сопротивление больше омического из-за явления поверхностного эффекта. Поверхностный эффект заключается в том, что ток вытесняется из центральных частей к периферии сечения проводника.
|
 Скачать 0.58 Mb.
Скачать 0.58 Mb.