Коллоквиум. Основные положения молекулярнокинетической теории. Основные положения молекулярнокинетической теории
 Скачать 0.92 Mb. Скачать 0.92 Mb.
|
|
1. Основные положения молекулярно-кинетической теории. Основные положения молекулярно-кинетической теории 1)Все вещества состоят из мельчайших частиц - атомов и молекул. 2)Молекулы и атомы любого вещества находятся в непрерывном хаотическом движении, которое называется тепловым движением. При нагревании вещества интенсивность движения частиц увеличивается. 3)Молекулы вещества взаимодействуют между собой с силами притяжения Fпр и отталкивания Fот . r = r0 , Fот = Fпр , Основное МКТ уравнение P=1/3m0nV2 r < r0 , Fот > Fпр , r > r0 , Fот < Fпр , r , F 0. 2. Термодинамическая система — это любая зона или пространство, ограниченное действительными или воображаемыми границами, выбранными для анализа энергии и ее преобразования. Границы ее могут быть неподвижными или подвижными. Газ в металлическом сосуде является примером системы с неподвижными границами. Для описания состояния термодинамической системы вводятся физические величины, которые называются термодинамическими параметрами или параметрами состояния системы. Обычно в качестве термодинамических параметров выбирают давление P, объем V и температуру T. Р  ассмотрим теперь изопроцессы для идеального газа: ассмотрим теперь изопроцессы для идеального газа:1)T = const – изотермический процесс. PV = const – закон Бойля-Мариотта 2  )P = const - изобарический процесс. )P = const - изобарический процесс.V/T=const закон Гей-Люссака. 3  )V = const – изохорический процесс )V = const – изохорический процессP /T= const - закон Шарля. 3.Идеальным газом называется газ, молекулы которого не взаимодействуют друг с другом на расстоянии и имеют исчезающе малые собственные размеры. Состояние заданной массы m идеального газа определяется значениями трёх параметров: давления P, объёма V, и температуры Т. Соотношение, устанавливающее связь между этими параметрами, имеет вид: PV=(m/M)RT - уравнение состояния идеального газа (уравнение Менделеева-Клапейрона) где М - масса 1 моля газа, R = 8,31 Дж/мольК универсальная газовая постоянная. Для одного моля газа уравнение состояния идеального газа примет вид: PV/T=R=const - уравнение Клапейрона 4. Закон распределения молекул идеального газа по скоростям определяет, какое число dN молекул однородного (p = const) одноатомного идеального газа из общего числа N его молекул в единице объёма имеет при данной температуре Т скорости, заключенные в интервале от v до v + dv. dn/ndv=f(v) Максвелловское распределение молекул по их скоростям: 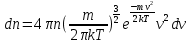 где n – число молекул в единице объема, dn – число молекул в единице объема, имеющих скорость в интервале от v до v + dv, m – масса молекулы, k – постоянная Больцмана, T – температура. Haиболее вероятная скорость молекул 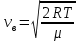 Средняя квадратичная скорость молекул 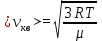 Средняя арифметическая скорость молекул 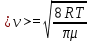 5. Функция распределения молекул по энергиям теплового движения: 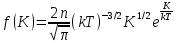 6. Эффективный диаметр молекулы — минимальное расстояние, на которое сближаются центры двух молекул при столкновении. При столкновении, молекулы сближаются до некоторого наименьшего расстояния, которое условно считается суммой радиусов взаимодействующих молекул. Средняя длина свободного пробега молекул газа Длина свободного пробега молекулы – это путь l, который молекула проходит между двумя последовательными соударениями. z - число столкновений N=nV=nπr^2L Z=(N/t)2^ ½=n2^ ½ * πδ^2(L/t) L 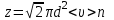 /t= /t=среднее число столкновений за секунду с 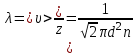 редняя длина свободного пробега, где d – эффек-й диаметр молекулы редняя длина свободного пробега, где d – эффек-й диаметр молекулы7 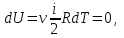 . Вследствие теплового движения молекул будет происходить процесс выравнивания концентраций, сопровождающийся переносом массы каждой из компонент в направлении убывания её концентрации. Этот процесс носит название диффузии. Диффузия наблюдается так же в жидких и твёрдых телах. . Вследствие теплового движения молекул будет происходить процесс выравнивания концентраций, сопровождающийся переносом массы каждой из компонент в направлении убывания её концентрации. Этот процесс носит название диффузии. Диффузия наблюдается так же в жидких и твёрдых телах.Поток молекул i – го вида через перпендикулярную к оси х поверхность S определяется выражением 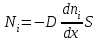 где D – коэффициент пропорциональности, называемый коэффициентом диффузии. Умножив обе части этого равенства на массу молекулы i – го вида mi, получим выражение для потока массы i – ой компоненты:  где i = nimi – парциальная плотность i – ой компоненты. Эти формулы - уравнения Фика Через площадку S возникает поток тепла, величина которого определяется формулой, называемой уравнением теплопроводности или законом Фурье:  Г  де dT/dx - градиент температуры, т.е. величина, показывающая, как быстро изменяется температура в де dT/dx - градиент температуры, т.е. величина, показывающая, как быстро изменяется температура в направлении оси х, (каппа) – коэффициент пропорциональности, зависящий от свойств среды и называемый коэффициентом теплопроводности. Перемещаясь вследствие теплового движения молекулы переносят запасённую ими энергию. Этот перенос энергии и обуславливает процесс теплопроводности в газах. И  сходя из упрощённых представлений, количество молекул, пролетающих через площадку S за секунду. сходя из упрощённых представлений, количество молекул, пролетающих через площадку S за секунду.Количество энергии, переносимое молекулами за секунду через площадку S в положительном направлении оси х, можно записать следующим образом: 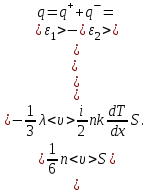 8. Сила трения между двумя слоями жидкости может быть вычислена по формуле 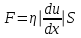 г 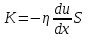 де - коэффициент вязкости, du/dx- градиент скорости, S – величина поверхности, по которой действует сила F. де - коэффициент вязкости, du/dx- градиент скорости, S – величина поверхности, по которой действует сила F.Уравнение вязкости 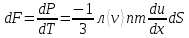 Механизм внутреннего трения в жидкостях и газах заключается в том, что хаотически движущиеся молекулы переносят импульс из одного слоя в другой, что приводит к выравниванию скоростей — это описывается введением силы трения. Молекулы одного слоя налетают на мол. соседнего слоя ...теряют часть импульса, соседний слой - приобретает. закон Ньютона для внутреннего трения. Знак плюс или минус принимается в зависимости от знака градиента скорости dv/dn. 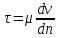 10. Внутренняя энергия идеального газа равна числу молекул газа, умноженному на среднюю кинетическую энергию одной молекулы.U = N < г > Закон равномерного распределения энергии по степеням свободы молекул: На каждую степень свободы молекулы приходится в среднем одинаковая кинетическая энергия 0.5 kT (k-постоянная Больцмана). Числом степеней свободы i системы называется количество независимых величин, с помощью которых может быть задано положение системы. < г >= (i/2) kT - Средняя кинетическая энергия молекул газа i = iпост+ iвращ+ iколеб - общее число степеней свободы молекул. Среднюю энергию молекулы можно представить в виде: < г > = < гпост> + < гвращ > + < гколеб > . При низких температурах ( Т < 1000К ) i = iпост+ iвращ Внутреннюя энергия идеального газа: 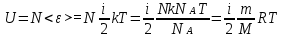 г 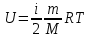 де де 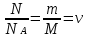 - число молей газа (количество вещества), - число молей газа (количество вещества), 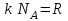 в 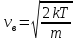 нутренняя энергия идеального газа нутренняя энергия идеального газа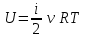 или 11. Термодинамика изотермического процесса: T=const. Закон, описывающий этот процесс, и его график в координатах (P,V). - 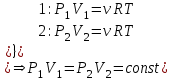 закон Бойля-Мариотта закон Бойля-МариоттаТак как T = const, то т. е. dU = 0 - изменение внутренней энергии газа при изотермическом процессе равно нулю. Тогда dQ = dA - Первое начало термодинамики при изотермическом процессе При изотермическом процессе вся теплота, сообщенная газу, идет на работу, совершаемую газом: Q = A. Работа, совершаемая газом при изотермическом процессе. Используя уравнение Менделеева-Клапейрона  представим элементарную работу в виде: представим элементарную работу в виде: Тогда  . .р  абота, совершаемая газом при изотермическом процессе абота, совершаемая газом при изотермическом процессеУчитывая то, что при изотермическом процессе  работу можно вычислить также по формуле: работу можно вычислить также по формуле: ; ;На графике (P,V) работа, совершаемая газом, численно равна площади (1-2-V1-V2) под кривой, описывающий изотермический процесс. 12. Термодинамика изохорического процесса: V=const Рассмотрим закон, описывающий этот процесс и его график в координатах (P,V). Этот закон является частным случаем уравнения состояния идеального газа: PV = RT. Закон Шарля:  Так как V=const, то dV=0 и dA=PdV=0, т.е A  =0 - работа совершаемая газом при изохорическом процессе равна нулю. Тогда =0 - работа совершаемая газом при изохорическом процессе равна нулю. Тогда dQ=dU - первое начало термодинамики для изохорического процесса. Поскольку количество теплоты, сообщенное газу, равно dQ=  *CvdT, где *CvdT, где 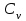 - молярная теплоёмкость газа при постоянном объёме, то мы получаем полезную формулу для подсчёта приращения внутренней энергии газа: - молярная теплоёмкость газа при постоянном объёме, то мы получаем полезную формулу для подсчёта приращения внутренней энергии газа: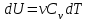 - изменение внутренней энергии газа - изменение внутренней энергии газа Сравнивая эту формулу с другой формулой 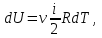 получим выражение для молярной теплоёмкости газа при постоянном объёме: 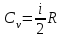 13. Термодинамика изобарического процесса: P=const. Соотношение Майера Сначала рассмотрим закон, описывающий этот процесс и его график в координатах (P,V).  - закон Гей-Люссака. Теперь работа, совершаемая газом, dA=PdV≠0 -приращение внутренней энергии газа тоже не равно нулю dU≠0, и первое начало термодинамики не меняет своего вида:dQ=dU+dA - первое начало термодинамики для изобарического процесса. Формула для подсчёта теплоты теперь примет вид  где Cp- молярная теплоёмкость газа при постоянном давлении. где Cp- молярная теплоёмкость газа при постоянном давлении.Приращение внутренней энергии запишем в виде  Работa, совершаемую газом:  Уравнение Менделеева-Клапейрона  дифференциальное уравнение которого при P=const дает  Из выражения для работы следует размерность и физический смысл универсальной газовой постоянной R: У   ниверсальная газовая постоянная R численно равно работе, совершённой одним молем газа при изобарическом процессе при увеличении его температуры на один градус. ниверсальная газовая постоянная R численно равно работе, совершённой одним молем газа при изобарическом процессе при увеличении его температуры на один градус.Изобарический процесс. Подставляя полученные выражения для dQ, dU, dA в первое начало термодинамики, получим:  Сократить на dT, получим соотношение между молярными теплоёмкостями газа при постоянном объёме Cv и постоянном давлении Cp: Сократить на dT, получим соотношение между молярными теплоёмкостями газа при постоянном объёме Cv и постоянном давлении Cp: Cp= Cv+R - соотношение Майера. Cv=(i/2)R, получим аналогичное выражение для Cp Cp=((i+2)/2)R Выражение для отношения моляр-х теплоёмкостей Cp и Cv: Д  ля двухатомных молекул при невысоких температурах i = 5, тогда γ=1,4. ля двухатомных молекул при невысоких температурах i = 5, тогда γ=1,4.Работа, совершаема газом при изобарическом процессе (P=const):   работа, совершаемая газом при изобарическом процессе. На графике (P,V) работа, совершаемая газом, численно равна площади прямоугольника 1-2-V1-V2, построенного под изобарой  14-15. . Термодинамика адиабатического процесса: dQ=0 А  диабатическийпроцесс - это процесс, протекающий без теплообмена с окружающей средой. Поскольку dQ = 0, то первое начало термодинамики примет вид:dU+dA=0 диабатическийпроцесс - это процесс, протекающий без теплообмена с окружающей средой. Поскольку dQ = 0, то первое начало термодинамики примет вид:dU+dA=0 Работа, совершаемая газом:  или работа для конечного адиабатического процесса:  - -Исходя из dU + dA = 0, выведем закон, которому удовлетворяют параметры газа при адиабатическом процессе. Для этого dU и dA представим в виде  Подставив это выражение в dU + dA = 0, получим дифференциальное уравнение:  к   оторое, разделив на СV T и используя соотношения оторое, разделив на СV T и используя соотношения  можно записать в виде  . .Это дифференциальное уравнение приводится к полному дифференциалу:  уравнение адиабатического процесса в переменных(T,V):  Воспользовавшись уравнением Менделеева-Клапейрона PV = RT, можно перейти к переменным (P,V) и (T,P). Например, из  Подставляя это в уравнение Подставляя это в уравнение  , получим , получим   или  - уравнение Пуассона, где - уравнение Пуассона, где  -коэффициент Пуассона. -коэффициент Пуассона. уравнения адиабаты. 16. Второе начало термодинамики: Невозможно построить периодически действующую тепловую машину, которая бы всю подводимую к ней теплоту превращала в работу, т.е. всегда  Карно предложил идеальный цикл, который даёт максимальное КПД т.е. Карно предложил идеальный цикл, который даёт максимальное КПД т.е.  . Этот цикл состоит из двух изотерм и двух адиабат и носит название цикла Карно. . Этот цикл состоит из двух изотерм и двух адиабат и носит название цикла Карно.1→2- изотермическое расширение при T1 2→3- адиабатическое расширение, dQ=0 3→4- изотермическое сжатие при T2 4→1- изотермическое сжатие, dQ=0. При изотермическом процессе внутренняя энергия идеального газа остаётся постоянной. Поэтому количество полученной газом теплоты Q1 равно работе A12, совершаемой газом при переходе из состояния 1 в состояние 2. Эта работа равна  , где m – масса идеального газа в тепловой машине. , где m – масса идеального газа в тепловой машине.Количество отдаваемой холодильнику теплоты Q2 равно работе A34:  Для того чтобы цикл был замкнутым, состояния 1 и 4, 2 и 3 должны лежать на одной и той же адиабате:  , , Разделив одно соотношение на другое, приходим к условию замкнутости цикла: V2/V1=V3/V4 Теперь подставляя Q1 и Q2 в выражение для КПД, получим КПД цикла Карно:  где T1 - температура нагревателя, T2 - температура холодильника. КПД цикла Карно является максимальным КПД из всех возможных циклов, осуществляемых в данных температурных интервалах T1 и T2. В общем случае при возможности необратимого цикла Карно это соотношение примет вид: где T1 - температура нагревателя, T2 - температура холодильника. КПД цикла Карно является максимальным КПД из всех возможных циклов, осуществляемых в данных температурных интервалах T1 и T2. В общем случае при возможности необратимого цикла Карно это соотношение примет вид: , ,  , или , или  Для обратимого цикла Карно: Для обратимого цикла Карно:  для необратимого цикла Карно: для необратимого цикла Карно:  17.  основное уравнение молекулярно-кинетической теории ( уравнение Клаузиуса ) Обратимым термодинамическим процессом называется термодинамический процесс, допускающий возможность возвращения системы в первоначальное состояние без того, чтобы в окружающей среде остались какие-либо изменения. Необходимым и достаточным условием обратимости термодинамического процесса является его равновесность. 2. Необратимым термодинамическим процессом называется термодинамический процесс, не допускающий возможности возвращения системы в первоначальное состояние без того, чтобы в окружающей среде остались какие-либо изменения. Все реальные процессы протекают с конечной скоростью. Они сопровождаются трением, диффузией и теплообменом при конечной разности между температурами системы и внешней среды. Следовательно, все они неравновесны и необратимы Физическим смыслом понятия энтропии является мера хаоса в системе; мера той энергии, которая рассеивается в виде тепла и не превращается в работу ("связанная энергия"). Энтропия является функцией состояния системы и не зависит от пути перехода. 1)Энтропия – функция состояния; она имеет ту же размерность, что и теплоемкость: 2) Энтропия– понятие вероятностное, поэтому и второй закон термодинамики имеет статистический характер, энтропия связана с термодинамической вероятностью в формуле Больцмана: S = kℓnW, где k – постоянная Больцмана; k = 1,38 × 10-23 Дж/K; w – термодинамическая вероятность – число микросостояний, при помощи которых реализуется данное макросостояние. 3) Энтропия – экстенсивное свойство системы, зависящее от количества вещества в системе Увеличение массы в n раз во столько же раз увеличивает энтропию. 4) Энтропия зависит от агрегатного состояния вещества. 5) S– величина аддитивная S = S1 + S2 + … Sn. основное уравнение молекулярно-кинетической теории ( уравнение Клаузиуса ) Обратимым термодинамическим процессом называется термодинамический процесс, допускающий возможность возвращения системы в первоначальное состояние без того, чтобы в окружающей среде остались какие-либо изменения. Необходимым и достаточным условием обратимости термодинамического процесса является его равновесность. 2. Необратимым термодинамическим процессом называется термодинамический процесс, не допускающий возможности возвращения системы в первоначальное состояние без того, чтобы в окружающей среде остались какие-либо изменения. Все реальные процессы протекают с конечной скоростью. Они сопровождаются трением, диффузией и теплообменом при конечной разности между температурами системы и внешней среды. Следовательно, все они неравновесны и необратимы Физическим смыслом понятия энтропии является мера хаоса в системе; мера той энергии, которая рассеивается в виде тепла и не превращается в работу ("связанная энергия"). Энтропия является функцией состояния системы и не зависит от пути перехода. 1)Энтропия – функция состояния; она имеет ту же размерность, что и теплоемкость: 2) Энтропия– понятие вероятностное, поэтому и второй закон термодинамики имеет статистический характер, энтропия связана с термодинамической вероятностью в формуле Больцмана: S = kℓnW, где k – постоянная Больцмана; k = 1,38 × 10-23 Дж/K; w – термодинамическая вероятность – число микросостояний, при помощи которых реализуется данное макросостояние. 3) Энтропия – экстенсивное свойство системы, зависящее от количества вещества в системе Увеличение массы в n раз во столько же раз увеличивает энтропию. 4) Энтропия зависит от агрегатного состояния вещества. 5) S– величина аддитивная S = S1 + S2 + … Sn.18. Уравнение Ван-Дер-Вальса  где а и б постоянные Ван-дер-Вальса определяемые для каждого газа экспериментально, б примерно в 4 раза больше объему молекул где а и б постоянные Ван-дер-Вальса определяемые для каждого газа экспериментально, б примерно в 4 раза больше объему молекул 19. Реальные газы отличаются от идеальных тем, что молекулы этих газов имеют конечные собственные объемы и связаны между собой сложными силами взаимодействия. При высоких давлениях и достаточно низких температурах реальные газы конденсируются, т. е. переходят в жидкое состояние, чего принципиально не может быть с идеальными газами 20. ΔAвнеш = σΔS. Коэффициент σ называется коэффициентом поверхностного натяжения (σ > 0). Таким образом, коэффициент поверхностного натяжения равен работе, необходимой для увеличения площади поверхности жидкости при постоянной температуре на единицу. В СИ коэффициент поверхностного натяжения измеряется в джоулях на метр квадратный (Дж/м2) или в ньютонах на метр (1 Н/м = 1 Дж/м2). Следовательно, молекулы поверхностного слоя жидкости обладают избыточной по сравнению с молекулами внутри жидкости потенциальной энергией. Потенциальная энергия Eр поверхности жидкости пропорциональна ее площади: Eр = Aвнеш = σS. Текучесть жидкости обусловлена подвижностью молекул, составляющих жидкость. Пове́рхностно-акти́вные вещества́ (ПАВ) — химические соединения, которые, концентрируясь на поверхности раздела термодинамических фаз, вызывают снижение поверхностного натяжения.(мыло) 21. Если жидкость контактирует с твёрдым телом, то существуют две возможности: 1)молекулы жидкости притягиваются друг к другу сильнее, чем к молекулам твёрдого тела. В результате силы притяжения между молекулами жидкости собирают её в капельку. Так ведёт себя ртуть на стекле, вода на парафине или «жирной» поверхности. В этом случае говорят, что жидкость не смачивает поверхность; 2)молекулы жидкости притягиваются друг к другу слабее, чем к молекулам твёрдого тела. В результате жидкость стремится прижаться к поверхности, расплывается по ней. Так ведёт себя ртуть на цинковой пластине, вода на чистом стекле или дереве. В этом случае говорят, что жидкость смачивает поверхность. Несмачивание - физическое явление отсутствия смачивания жидкостью поверхности материала. Смачивание — физическое взаимодействие жидкости с поверхностью твёрдого тела или другой жидкости. Смачивание бывает двух видов -Иммерсионное (вся поверхность твёрдого тела контактирует с жидкостью ) -Контактное (состоит из 3х фаз - твердая, жидкая, газообразная) 22. Это давление, называемое давлением Лапласа, зависит от 23. Твердые тела можно классифицировать по различным признакам.1) По структурному признаку их можно разделить на три класса: аморфные, кристаллические и нанодисперсные твердые вещества. Кристаллические вещества – твердые тела, в которых атомы расположены закономерно, образуя трёхмерно-периодическую пространственную укладку – кристаллическую решётку. Структурные дефекты - это энергетически возбужденные состояния кристаллической решетки, связанные с нарушением строгой регулярности и способа заполнения узлов кристаллической решетки. Примесные дефекты, как следует из определения, обусловлены присутствием чужеродных атомов или молекул. Собственные дефекты не меняют качественного состава кристалла (меняться может лишь количественный состав). Их возникновение связано с влиянием температуры, механических радиационных и других видов воздействия на твердую фазу. 1) Точечные (нульмерные) дефекты малы во всех измерениях, их размеры по всем направлениям не превышают нескольких атомных диаметров. Они состоят из одного атома (если это атом примеси) или дефектной позиции (если кристалл не содержит примесных атомов). 2) Линейные (одномерные) дефекты – это нарушение линейной последовательности узлов решетки, вдоль которой обрывается периодичность структуры. 3) Поверхностные (двумерные) дефекты – это ошибки в наложение слоев атомов, а также границы, отделяющие различные области идеальной или близкой к идеальной периодической структуры кристалла. 4) Объёмные (трёхмерные дефекты) имеют в трех измерениях сравнительно большие размеры, несопоставимые с величинами атомных диаметров. 24. При любой температуре в твердых телах, как и в жидкостях, существует некоторое количество атомов с высокой кинетической энергией, достаточной для преодоления потенциального поверхностного барьера. Этот процесс, как мы знаем, называется сублимацией,или возгонкой. Переход вещества из твердой фазы в жидкую, как мы уже знаем, называется плавлением. Процесс кристаллизациивещества из жидкой фазы всегда сопровождается выделением теплоты кристаллизации, которая совпадает по величине с теплотой плавления Этот процесс характеризуется изменением температуры системы. Количество теплоты определяется по формуле Энергия, которая тратится на разрушение кристаллической решетки вещества, определяется по формуле 25. Фазой называется термодинамическое равновесное состояние вещества, отличающееся по физическим свойствам от других возможных равновесных состояний того же вещества. Переход вещества из одной фазы в другую – фазовый переход - всегда связан с качественными изменениями свойств тела. Фазовый переход 1 рода – сопровождается поглощением или выделением теплоты, изменением объема и протекает при постоянной температуре.Примеры: плавление, кристаллизация, испарение, сублимация (возгонка) и др. Фазовые переходы 2 рода – протекают без выделения или поглощения тепла, с сохранением величины объема, но скачкообразным изменением теплоемкости. |
