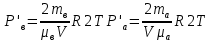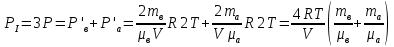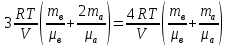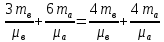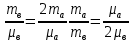Опорный конспект по решению задач. Основные теоретические сведения
 Скачать 170.12 Kb. Скачать 170.12 Kb.
|
|
Основные теоретические сведения Состояние газа характеризуется совокупностью трех физических величин или термодинамических параметров: объемом газа V, давлением Р и температурой Т. Состояние газа, при котором эти параметры остаются постоянными считают равновесным состоянием. В этом состоянии параметры газа связаны между собой уравнением состояния. Самый простой вид уравнение состояния имеет для идеального газа. Идеальным газом называют газ, молекулы которого не имеют размеров (материальные точки) и взаимодействуют друг с другом лишь при абсолютно упругих соударениях (отсутствует межмолекулярное притяжение и отталкивание). Реальные газы тем точнее подчиняются законам идеальных газов, чем меньше размеры их молекул (т.е. газ одноатомный), и чем больше он разряжен. Уравнение состояния идеального газа или уравнение Менделеева-Клапейрона имеет вид: 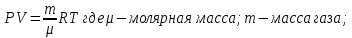 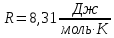 - универсальная газовая постоянная - универсальная газовая постояннаяИз этого закона вытекает, что для двух произвольных состояний газа справедливо равенство, называемое уравнением Клапейрона: 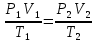 Так же для идеальных газов имеют место следующие экспериментальные законы: Закон Бойля — Мариотта: 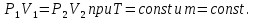 Закон Гей-Люссака: 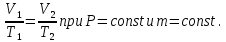 Закон Шарля: Закон Шарля: 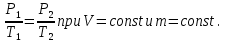 Если в сосуде находится смесь нескольких газов, не вступающих друг с другом в химические реакции, то результирующее давление определяется по закону Дальтона: давление смеси равно сумме давлений, производимых каждым газом в отдельности, как если бы он один занимал весь сосуд. Если в сосуде находится смесь нескольких газов, не вступающих друг с другом в химические реакции, то результирующее давление определяется по закону Дальтона: давление смеси равно сумме давлений, производимых каждым газом в отдельности, как если бы он один занимал весь сосуд. Р = Р1 + Р2 +... + РN Задачи, решение которых основывается на данных уравнениях, можно разделить на две группы: задачи на применение уравнения Менделеева-Клапейрона. задачи на газовые законы. ЗАДАЧИ НА ПРИМЕНЕНИЕ УРАВНЕНИЯ МЕНДЕЛЕЕВА-КЛАПЕЙРОНА. Уравнение Менделеева-Клапейрона применяют тогда, когда дано только одно состояние газа и задана масса газа (или вместо массы используют количество вещества или плотность газа). масса газа не задана, но она меняется, то есть утечка газа или накачка. При решении задач на применение равнения состояния идеального газа надо помнить: если дана смесь газов, то уравнение Менделеева-Клапейрона записывают для каждого компонента в отдельности. Связь между парциальными давлениями газов, входящих в смесь и результирующим давлением смеси, устанавливается законом Дальтона. если газ меняет свои термодинамические параметры или массу, уравнение Менделеева-Клапейрона записывают для каждого состояния газа в отдельности и полученную систему уравнений решают относительно искомой величины. P.S. Необходимо пользоваться только абсолютной температурой и сразу же переводить значения температуры по шкале Цельсия в значения по шкале Кельвина. В задачах, где рассматривается движение сосуда с газом (пузырька воздуха, воздушного шара) к уравнению газового состояния добавляют уравнения механики. если между газами происходит реакция, то надо составить уравнение реакции и определить продукты реакции ПЕРВЫЙ ТИП ЗАДАЧ: НЕТ ИЗМЕНЕНИЯ МАССЫ Определить давление кислорода в баллоне объемом V = 1 м3 при температуре t=27 °С. Масса кислорода m = 0,2 кг.
Баллон емкостью V= 12 л содержит углекислый газ. Давление газа Р = 1 МПа, температура Т = 300 К. Определить массу газа.
При температуре Т = 309 К и давлении Р = 0,7 МПа плотность газа ρ = 12 кг/м3. Определить молярную массу газа.
Какова плотность водорода при нормальном атмосферном давлении и температуре 20°С.
До какой температуры Т1 надо нагреть кислород, чтобы его плотность стала равна плотности водорода при том же давлении ,но при температуре Т2 = 200 К?
В сосуде объемом 4·10-3 м3 находится 0,012 кг газа при температуре 177°С. При какой температуре плотность этого газа будет равна 6·10-6 кг /см3, если давление газа остается неизменным.
Смесь газов В баллоне объемом 25 литров находится 20 г азота и 2 г гелия при 301К. Найдите давление в баллоне.
Определить плотность смеси, состоящей из 4 граммов водорода и 32 граммов кислорода при давлении 7°С и давлении 93кПа?
Сосуд емкостью 2V разделен пополам полупроницаемой перегородкой. В одной половине находится водород массой mВ и азот массой mА. В другой половине вакуум. Во время процесса поддерживается постоянная температура Т. Через перегородку может диффундировать только водород. Какое давление установиться в обеих частях сосуда?
Вакуумированный сосуд разделен перегородками на три равных отсека, каждый объемом V. В средний отсек ввели одинаковые массы кислорода, азота и водорода. В результате чего давление в этом отсеке стало равно Р. Перегородка I проницаема только для молекул водорода, перегородка II проницаема для молекул всех газов. Найти давления Р1 Р2 и Р3, установившиеся в каждом отсеке, если температура газа поддерживается постоянной и равной Т.
С химическими реакциями В сосуде находится смесь азота и водорода. При температуре Т, когда азот полностью диссоциирован на атомы, давление равно Р (диссоциацией водорода можно пренебречь). При температуре 2Т, когда оба газа полностью диссоциированы, давление в сосуде 3Р. Каково отношение масс азота и водорода в смеси?
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

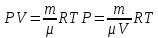
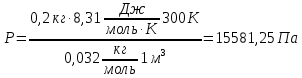
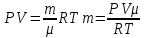
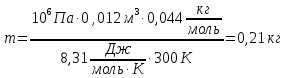
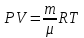
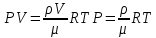
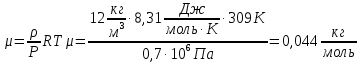
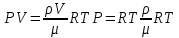
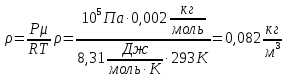
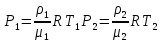

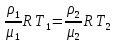
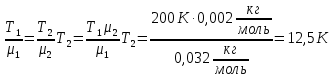
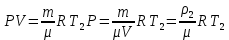
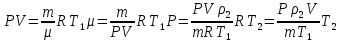
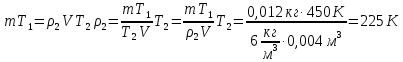
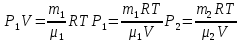
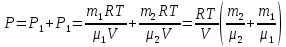
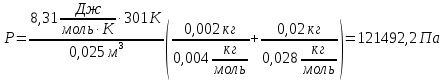
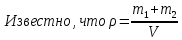

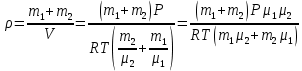
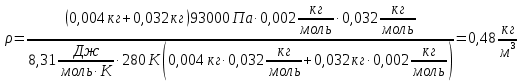

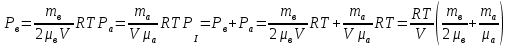
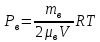

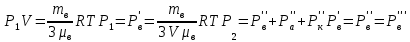
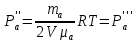
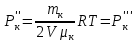
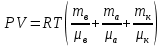
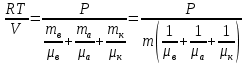
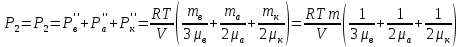
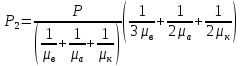
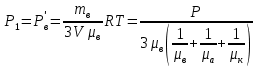
 ри температуре Т параметры газов в сосуде следующие:
ри температуре Т параметры газов в сосуде следующие: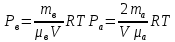
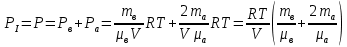
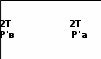 ри температуре 2Т параметры газов в сосуде следующие:
ри температуре 2Т параметры газов в сосуде следующие: