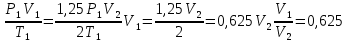Опорный конспект по решению задач. Основные теоретические сведения
 Скачать 170.12 Kb.
|
Когда из сосуда выпустили некоторое количество газа, давление в нем упало на 40%, а абсолютная температура на 20%. Какую часть газа выпустили?
В сосуде объемом V = 0,5 л находится идеальный газ при давлении Р1=1 атм. и температуре t = 27 °С. Сколько молекул газа нужно выпустить из сосуда, чтобы давление в нем уменьшилось в 2 раза? Температура газа не изменяется.
В пустой сосуд объемом V нагнетают воздух при помощи поршневого насоса, объем цилиндра которого V0. Каким будет давление воздуха в сосуде после N качаний?
Компрессор засасывает из атмосферы каждую секунду 3 литра воздуха, которые подаются в баллон емкостью 45 литров. Через сколько времени давление в баллоне будет превышать атмосферное в 9 раз? Начальное давление в баллоне равно атмосферному.
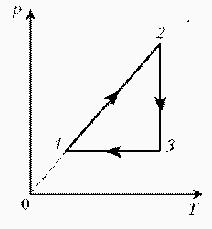
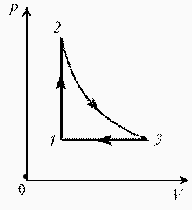
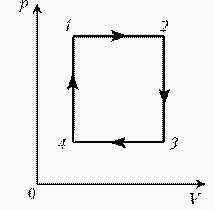
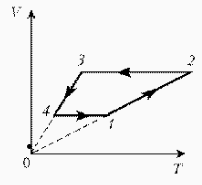
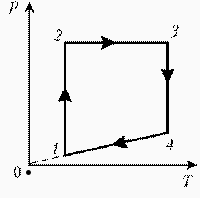
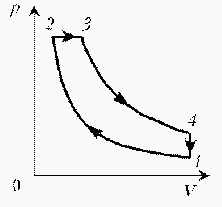
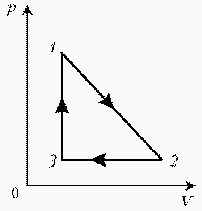
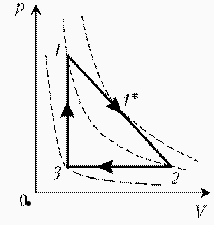
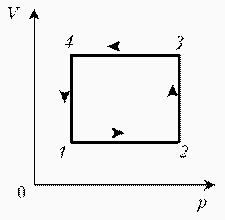
Задачи на применение газовых законов. Газовые законы применяют тогда, когда даны два состояния газа и при переходе газа из одного состояния в другое масса газа не меняется. ГРАФИЧЕСКИЕ ЗАДАЧИ НА ГАЗОВЫЕ ЗАКОНЫ На диаграмме РT изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме Р,V.
Для постоянной массы идеального газа представлен цикл на диаграмме РV. Изобразить этот цикл на диаграмме VT.
Изобразите на диаграмме РТ цикл постоянной массы идеального газа, представленный на диаграмме РV.
Какая из двух линий графика соответствует большему давлению данной массы идеального газа? 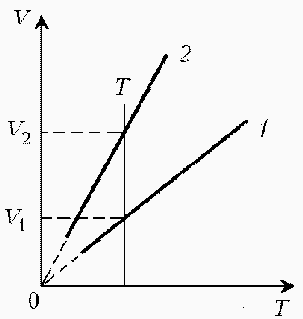 Прежде всего установим, что это за линии. Эти линии выражают прямо пропорциональную зависимость между объемом газа и его температурой, а это возможно для идеального газа только при изобарическом процессе, следовательно, изображенные линии графика – изобары. Проведем изотерму до пересечения с обеими изобарами, а точки их пересечения спроецируем на ось ординат (объемов). Из построения видно, что V2 > V1. Поскольку при изотермическом процессе газ подчиняется закону Бойля–Мариотта: Р1V1 = Р2V2, то Р1 > Р2. При нагревании идеального газа постоянной массы получена зависимость Р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа? 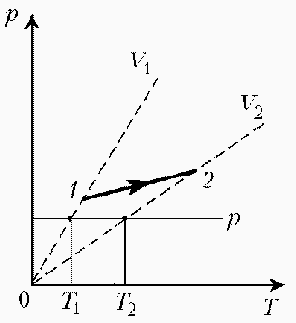 Прежде всего обратим внимание на то, что линия графика не описывается ни одним из изопроцессов («неявная форма»). Проведем через начальную и конечную точки линии графика две изохоры. Проведя еще изобару (или, как вариант, изотерму) и, спроецировав точки ее пересечения с изохорами на ось Т, убедимся, что Т2 > Т1. При изобарическом процессе, по закону Гей-Люссака, V T, следовательно, V2 > V1. А так как плотность и объем связаны обратной зависимостью (при данной массе), то ρ1 > ρ2, откуда следует, что газ расширялся, а значит, его плотность уменьшилась. Как менялась температура постоянной идеального массы газа на протяжении цикла?
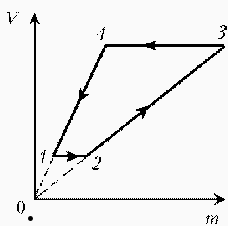
Идеальный газ с молярной массой М участвует в изотермическом процессе. При этом получена зависимость между объемом V и давлением р. Представьте этот цикл на диаграмме V, m.
Аналитические задачи на газовые законы При решении аналитических задач на газовые законы надо: Убедиться, что при изменении состояния масса газа остается постоянной. Сделать схематический чертеж, на котором условно отметить состояния газа параметрами Р, V, Т. Записать закон Клапейрона для данных двух состояний. Если какой-либо параметр при переходе газа из одного состояния в другое остается неизменным (могут меняться все три параметра), то уравнение Клапейрона перевести в закон Бойля — Мариотта, Гей-Люссака или Шарля. В случае, когда газ заключен в цилиндрический сосуд и объем газа меняется только за счет изменения высоты его столба h, уравнение Клапейрона можно сразу записывать в виде: 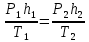 Используя условия задачи, определить термодинамические параметры, выразив их через заданные величины. И если газ граничит с жидкостью, то особое внимание следует обратить на определение давления. Для его определения тех случаях, когда газ производит давление на жидкость, следует использовать закон Паскаля: провести нулевой уровень через границу, отделяющую газ от жидкости, и записать уравнение равновесия жидкости. Полученную систему уравнений решить относительно неизвестной величины. P.S. Если в задаче рассматривают состояния нескольких газов, отделенных друг от друга поршнями или входящих в состав смеси, то все указанные действия нужно проделать для каждого газа отдельно. В задачах на газовые законы используется только абсолютная температура. При увеличении абсолютной температуры газа в 2 раза давление увеличилось на 25%. во сколько раз изменился объем газа?
Газ изотермически сжат от объема V1 = 8 л до объема V2 = 6 л. Давление при этом возросло на Р = 4∙103 Па. Определить первоначальное давление. Запишем уравнение Клапейрона и, так как процесс изотермический, переведем его в закон Бойля-Мариотта 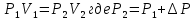 Поэтому можно записать: 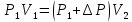 Отсюда находим первоначальное давление: 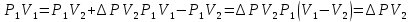 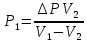 И объемы газов можно оставить в литрах, не переводить в систему СИ. При нагревании газа при постоянном давлении на 1К его объем увеличился на 5% от первоначального. При какой температуре находился газ? 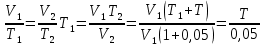 Сколько ртути войдет в стеклянный баллончик объемом V0, нагретый до Т0, если плотность ртути при температуре Т равна ρ. 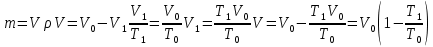 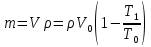 Закрытый с обоих концов цилиндрический сосуд разделен на две равные части теплонепроницаемым поршнем. Длина каждой части 42см. В обеих половинках находится одинаковое количество азота при температуре 27°С и давлении 1 атмосфера. На сколько надо нагреть газ в одной части сосуда, чтобы поршень переместился на 2 см?  Для газа в отделе I: 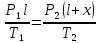 Для газа в отделе II: 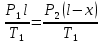 Отсюда следует: 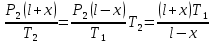 Объем баллона, содержащего газ под давлением 1,2·105 Па составляет 6 литров. Каким станет давление газа, если этот баллон соединить с другим баллоном объем которого 10 литров и он практически не содержит газа. 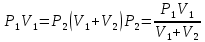 Два одинаковых стеклянных шара соединены трубкой. При 0° С капелька ртути находится посередине трубки. Объем воздуха в каждом шаре и части трубки У= 200 см3 . На какое расстояние х сместится капелька, если один шар нагреть на 2° С, а другой на столько же охладить? Поперечное сечение трубки S=20 мм2  Для газа в отделе I:     | |||||||||||||||||||||||||||||||||||||||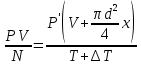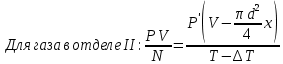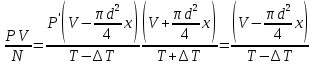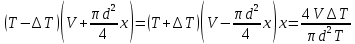
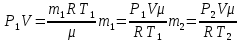
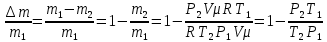
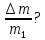
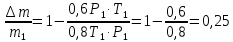
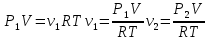
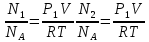
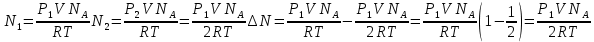
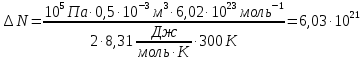
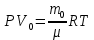
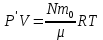
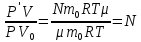
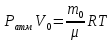
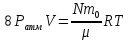
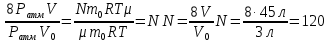
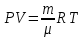
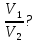
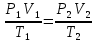С учетом данных, уравнение принимает вид: