шпора. Основные положения молекулярнокинетической теории
 Скачать 13.84 Mb. Скачать 13.84 Mb.
|
|
1. Основные положения молекулярно-кинетической теории. Молекулярно-кинетическая теория истолковывает свойства тел, которые непосредственно наблюдаются на опыте (давление, температуру и т.п.), как суммарный результат действия молекул. При этом она пользуется статистическим методом, интересуясь не движением отдельных молекул, а лишь средними величинами, которые характеризуют движение огромной совокупности частиц. Отсюда другое её название – статистическая физика. Термодинамика изучает макроскопические свойства тел, не интересуясь их микроскопической картиной. В основе термодинамики лежит несколько фундаментальных законов (называемых началами термодинамики), установленных на основании обобщения большой совокупности опытных фактов. Термодинамика и молекулярно-кинетическая теория взаимно дополняют друг друга, образуя по существу единое целое. Основные положения молекулярно-кинетической теории 1)Все вещества состоят из мельчайших частиц - атомов и молекул. 2)Молекулы и атомы любого вещества находятся в непрерывном хаотическом движении, которое называется тепловым движением. При нагревании вещества интенсивность движения частиц увеличивается. 3)Молекулы вещества взаимодействуют между собой с силами притяжения Fпр и отталкивания Fот . r = r0 , Fот = Fпр , r < r0 , Fот > Fпр , r > r0 , Fот < Fпр , r , F 0.  Характер движения молекул зависит от агрегатного состояния вещества. 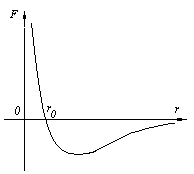 Движение молекул газов сводится к хаотическому поступательному движению. Скорость молекул газов зависит от температуры. Масса молекулы: Молекулярная масса вещества – масса молекулы вещества, выраженная в а.е.м. Атомная единица массы (а.е.м.) – единица массы, равная 1/12 массы атома С12. Моль – количество вещества, в котором содержится число молекул, равное числу атомов в 0,012 кг изотопа углерода С12. Число частиц, содержащихся в моле вещества, называется числом Авогадро: NA = 6,023 1023 моль-1 Молярная масса М – масса моля вещества. Зная число Авогадро, можно найти значение а.е.м. 0,012 = NA 12 1 а.е.м., 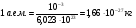 Размеры молекулы: Линейные размеры молекул воды приблизительно равны 3 10-10 м. 2. Термодинамические параметры. Уравнение состояния идеального газа Для описания состояния термодинамической системы вводятся физические величины, которые называются термодинамическими параметрами или параметрами состояния системы. Обычно в качестве термодинамических параметров выбирают давление P, объем V и температуру T. 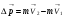 Температура – это макроскопический параметр, характеризующий различную степень нагретости тел. Это одна из макроскопических характеристик внутреннего состояния тел. Понятие температуры имеет смысл для равновесных состояний термодинамической системы. Равновесным состоянием (состоянием термодинамического равновесия) называется состояние системы, не изменяющееся с течением времени (стационарное состояние), причем стационарность состояния не связана с процессами, происходящими во внешней среде. Равновесное состояние устанавливается в системе при постоянных внешних условиях и сохраняется в системе произвольно долгое время. Во всех частях термодинамической системы, находящейся в состоянии термодинамического равновесия, температура одинакова. В термодинамической шкале температур температура измеряется в кельвинах ( К ) и обозначается Т . 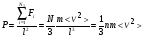 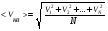 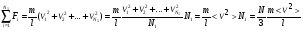 Соотношение, устанавливающее связь между параметрами состояния системы называется уравнением состояния термодинамической системы. Если какой либо из термодинамических параметров системы изменяется, то происходит изменение состояния системы, называемое термодинамическим процессом. Термодинамический процесс называется равновесным, если система бесконечно медленно проходит непрерывный ряд бесконечно близких термодинамических равновесных состояний. Изопроцессами называются термодинамические процессы, происходящие в системе с постоянной массой при каком либо одном постоянном параметре состояния. 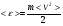 Идеальным газом называется газ, молекулы которого не взаимодействуют друг с другом на расстоянии и имеют исчезающе малые собственные размеры. Состояние заданной массы m идеального газа определяется значениями трёх параметров: давления P, объёма V, и температуры Т. Соотношение, устанавливающее связь между этими параметрами, имеет вид: PV=(m/M)RT - уравнение состояния идеального газа (уравнение Менделеева-Клапейрона) где М - масса 1 моля газа, R = 8,31 Дж/мольК универсальная газовая постоянная. Для одного моля газа уравнение состояния идеального газа примет вид: PV/T=R=const - уравнение Клапейрона.  Рассмотрим теперь изопроцессы для идеального газа: 1)T = const – изотермический процесс. PV = const – закон Бойля-Мариотта  2)P = const - изобарический процесс. V/T=const закон Гей-Люссака.  3)V = const – изохорический процесс P /T= const - закон Шарля. Запишем уравнение состояния идеального газа в другой форме. Введем новую постоянную величину: 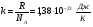 - постоянная Больцмана и перепишем уравнение Менделеева-Клапейрона в виде: PV=(m/M)NAkT Учитывая, что (m/M)NA=N - число молекул в газе массы m, получим PV= nkT => P=(N/V)kT Так как N/V=n - число молекул в единице объема или концентрация молекул, то P=nkT - другая форма записи уравнения состояния идеального газа. 3. Основное уравнение молекулярно – кинетической теории газов. Возьмем сосуд в форме куба с ребром L с газом и определим давление P газа на стенки сосуда. 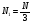 1)Вдоль оси х движется одна треть всех молекул, т.е. ; 2)Удар молекул о стенку Q идеально упругий и молекулы проходят расстояние, равное размеру куба, не испытывая соударений. 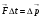 Импульс силы, полученный стенкой при ударе молекулы, определим из второго закона Ньютона: где - изменение импульса молекулы, m – масса молекулы. 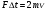 Одна молекула одна молекула за время t передает стенке импульс силы ,а за время t=1сек передаёт стенке импульс силы равный F*1=2mVk, где k – число ударов молекул за 1 сек. Так как 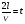 - промежуток времени между двумя последовательными ударами,. то K=1/t=V/2L, тогда F*1=m V2/L - промежуток времени между двумя последовательными ударами,. то K=1/t=V/2L, тогда F*1=m V2/L Теперь подсчитаем суммарный импульс силы, который передают стенке N1 молекул, движущихся вдоль оси x, за 1 сек средняя квадратичная скорость молекул газа 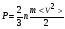 Давление, оказываемое газом на грань куба, где n – концентрация молекул. Запишем это выражение в виде: средняя кинетическая энергия поступательного движения молекулы. 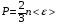 основное уравнение молекулярно-кинетической теории ( уравнение Клаузиуса ) С учетом уравнения состояния идеального газа: P=nkT 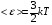 получаем выражение для средней кинетической энергии поступательного движения молекул: kT есть мера энергии теплового движения молекул. Молекулярно- кинетическое толкование абсолютной температуры: А. т. – есть величина, пропорциональная средней энергии поступательного движения молекул. 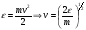 ---------------------- 4. Внутренняя энергия идеального газа. Закон равномерного распределения энергии по степеням свободы молекул газа. Внутренняя энергия идеального газа равна числу молекул газа, умноженному на среднюю кинетическую энергию одной молекулы.U = N < > 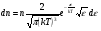 Законравномерного распределения энергии по степеням свободы молекул: На каждую степень свободы молекулы приходится в среднем одинаковая кинетическая энергия 0.5 kT (k-постоянная Больцмана).  Числом степеней свободы i системы называется количество независимых величин, с помощью которых может быть задано положение системы. < >= (i/2) kT - Средняя кинетическая энергия молекул газа i = iпост+ iвращ+ iколеб - общее число степеней свободы молекул. Среднюю энергию молекулы можно представить в виде: < > = < пост> + < вращ > + < колеб > . При низких температурах ( Т < 1000К ) i = iпост+ iвращ Внутреннюя энергия идеального газа: 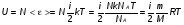 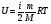 где 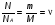 - число молей газа (количество вещества), - число молей газа (количество вещества), 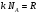 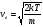 внутренняя энергия идеального газа 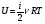 или ----------------------- 5. Максвелловское распределение молекул по их скоростям и энергиям 1)В результате столкновений молекул идеального газа, их скорости все время изменяются, но в газе создается некоторое стационарное распределение молекул по их скоростям . 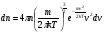 2)Максвелловское распределение молекул по их скоростям: где n – число молекул в единице объема, dn – число молекул в единице объема, имеющих скорость в интервале от v до v + dv, m – масса молекулы, k – постоянная Больцмана, T – температура. 3) кривые Максвелла для двух температур (T2>T1) 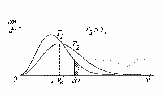 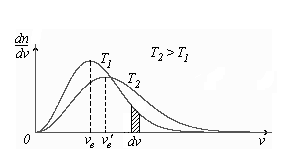 Физический смысл кривой Максвелла: dn/dv - число молекул, имеющих скорости в единичном интервале скоростей. Возьмем узкую полоску, которую можно считать прямоугольной. Ее площадь равна : (dn/dv)dv=dn Тогда площадь под всей кривой Максвелла равна n. 4)Новая функция: dn/ndv=f(v) -функция распределения Максвелла молекул по их скоростям График этой функции имеет аналогичный вид, но теперь площадь под кривой f(v) равна 1. dn/d - имеет смысл вероятности того, что молекула имеет скорость в интервале от V до V+dV. Согласно определению функции f(v) имеем dn/dn= f(v)dv f(v) - плотность вероятности того, что молекула имеет скорость в интервале от V до V+dV. 5)Распределениt молекул по их кинетической энергии . Для этого надо в распределении молекул по скоростям выразить V и dV через и d. 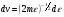 Максвелловское распределение молекул по их кинетическим энергиям: dn/nd=f()- функция распределения Максвелламолекул по их энергиям. 6. Характерные скорости молекул идеального газа
Это скорость молекул, при которой функция распределения f(V) имеет максимум. Возьмем производную от f(V), и приравняв ее нулю, получим уравнение для нахождения Vв: 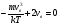 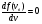 наиболее вероятная скорость молекул 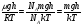 2) Для нахождения 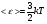 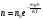 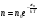  3) 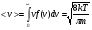 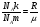 Воспользовавшись соотношением , формулы для характерных скоростей молекул 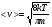 Haиболее вероятная скорость молекул 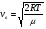 Средняя квадратичная скорость молекул 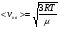 Средняя арифметическая скорость молекул 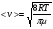 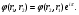 Опыт Штерна (1920г.) 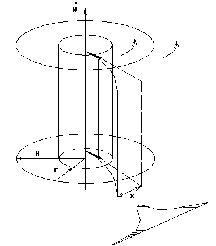 Два находящихся в вакууме жестко связанных между собой коаксиальных цилиндра, по оси которых натянута платиновая нить, покрытая серебром. Малый цилиндр радиуса r имеет вертикальную щель. Если по нити пропустить электрический ток, она будет нагреваться, серебро будет испарятся, его атомы будут пролетать через щель и осаждаться на большом цилиндре радиуса R, образуя изображение узкой щели в виде узкой полоски почернения серебра. Картина изменится, если установку привести во вращение с угловой скоростью . Изображение щели будет размыто с ярко выраженным максимумом. Атомы серебра имеют неодинаковые скорости, вследствие этого они имеют разные времена пробега и, поскольку цилиндр вращается, будут достигать его поверхности в разных точках. Наличие максимума в почернении, говорит о том, что имеется некоторая наиболее вероятная скорость атомов серебра. При этом простые вычисления дают возможность оценить скорость v атомов серебра. Приравнивая время пролета атомов между поверхностями цилиндров и время, в течение которого точки поверхности большого цилиндра сместились на x получим: 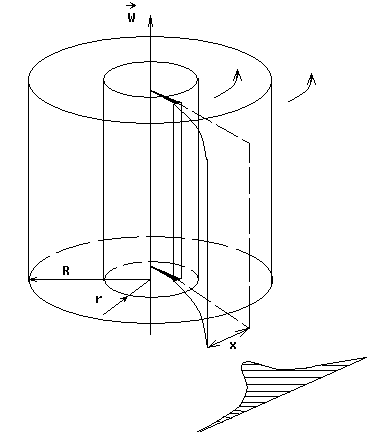 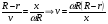 Скорость атомов серебра оказалась очень большой, порядка1000 м/с 7. Распределение Больцмана молекул по их потенциальным энергиям Если газ находится во внешнем силовом поле, то частицы газа обладают потенциальной энергией п . Рассмотрим распределение молекул идеального газа по высоте в однородном гравитационном поле. В этом случае для газа имеет место барометрическая формула: 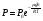 где Po - давление газа на поверхности Земли, P- давление газа на высоте h. P=nkT, Po=nokT получим распределение молекул по высоте в однородном гравитационном поле: распределение Больцмана молекул по их потенциальным энергиям распределение Максвелла 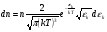 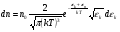 распределение Максвелла-Больцмана 8-10. Фазовое пространство – 6N мерное пространство, определяемое переменными, которые устанавливают параметры каждой частицы, т.е. координаты и проекции импульсов на эти координаты. Фазовый объем – объем элементарной квантовой ячейки больше или равен постоянно Планка в кубе. 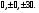 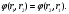 Бозоны – частицы, для которых волновые функции симметричны. Их состояния можно описать: Фотон, фонон, альфа частицы. Повышение одной частицей вероятности попадания другой такой же в это состояние. Фермионы – частицы, для которых волновые функции асимметричны. Их состояния можно описать: 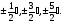 Электрон, протон, нейтрон 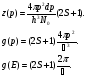 Плотность числа состояний частицы Функция распределения частиц по энергиям – дает среднее число частиц, в полосе энергетических состояний. Для нахождения пользуются статистическим методом, исследуют ферми-газ и бозе-газ. Функция Бозе-Энштейна: 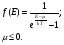 Для бозонов. Функция Ферми-Дирака: 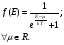 11.Средняя длина свободного пробега молекул газа Длина свободного пробега молекулы – это путь l, который молекула проходит между двумя последовательными соударениями. z - число столкновений N=nV=nπr^2L Z=(N/t)2^ ½=n2^ ½ * πδ^2(L/t) 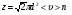 L/t= среднее число столкновений за секунду 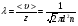 средняя длина свободного пробега, где d – эффек-й диаметр молекулы концентрацию газа определить из соотношения P = nkT, получим другую формулу для средней длины свободного пробега 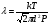 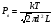 Состояние газа, при котором средняя длина свободного пробега молекул становится соизмеримой с размерами сосуда, называется вакуумом. 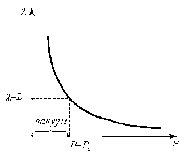 Вакуум: = L. давление вакуума   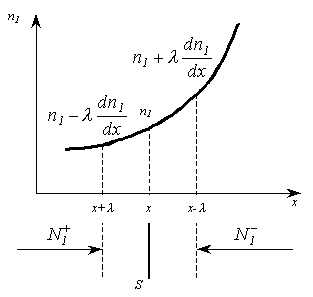 12.Теплопроводность газов В этом случае через площадку S возникает поток тепла, величина которого определяется формулой, называемой уравнением теплопроводности или законом Фурье:  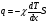 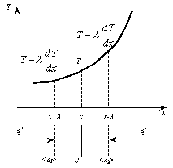 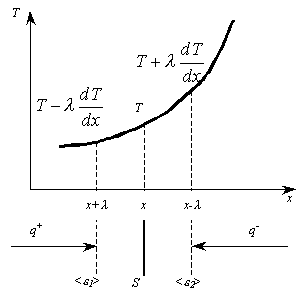 Где dT/dx - градиент температуры, т.е. величина, показывающая, как быстро изменяется температура в направлении оси х, (каппа) – коэффициент пропорциональности, зависящий от свойств среды и называемый коэффициентом теплопроводности. Знак минус в формуле отражает то обстоятельство, что тепло течёт в направлении убывания температуры. Перемещаясь вследствие теплового движения молекулы переносят запасённую ими энергию. Этот перенос энергии и обуславливает процесс теплопроводности в газах. 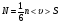 Исходя из упрощённых представлений, количество молекул, пролетающих через площадку S за секунду. Количество энергии, переносимое молекулами за секунду через площадку S в положительном направлении оси х, можно записать следующим образом: 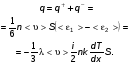 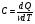 Сравнивая полученное выражение с законом Фурье, получим выражение для коэффициента теплопроводности через молекулярно-кинетические параметры газа: 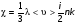 13.Диффузия и внутр. трение в ид. газах Вследствие теплового движения молекул будет происходить процесс выравнивания концентраций, сопровождающийся переносом массы каждой из компонент в направлении убывания её концентрации. Этот процесс носит название диффузии. Диффузия наблюдается так же в жидких и твёрдых телах. Поток молекул i – го вида через перпендикулярную к оси х поверхность S определяется выражением 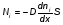 где D – коэффициент пропорциональности, называемый коэффициентом диффузии. Умножив обе части этого равенства на массу молекулы i – го вида mi, получим выражение для потока массы i – ой компоненты: 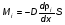 где i = nimi – парциальная плотность i – ой компоненты. Эти формулы - уравнения Фика. Поток молекул первой компоненты летящих через поверхность S в положительном направлении оси х, равен 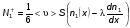 а соответствующий поток молекул первой компоненты, летящих в отрицательном направлении оси х равен разности этих потоков 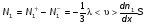 Таким образом, мы пришли к уравнению диффузии Фика, причём получили для коэффициента диффузии выражение 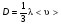 . .Сила трения между двумя слоями жидкости может быть вычислена по формуле 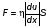 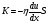 где - коэффициент вязкости, du/dx- градиент скорости, S – величина поверхности, по которой действует сила F. Уравнение вязкости 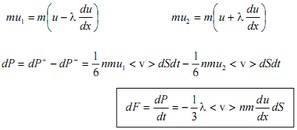 14.Первое начало термодинамики, теплоёмкость ид. Газа,работа газа при изменении объёма. Первое начало термодинамики. Количество теплоты, сообщённое газу, идёт на приращение внутренней энергии газа и на совершение газом работы над внешними телами. dQ=dU+dA - первое начало термодинамики. Физические величины, входящие в этот закон. а) Внутренняя энергия идеального газа равна 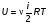 , где , где 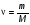 - количество вещества, i – число степеней свободы молекул газа. - количество вещества, i – число степеней свободы молекул газа.Тогда изменение внутренней энергии газа равно 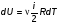 б) Вычислим теперь работу, совершаемую газом при изменении объёма. Для этого рассмотрим газ, находящийся в цилиндре под поршнем, который может свободно перемещаться. При нагревании давление газа P , будет оставаться постоянным, и, как видно из рисунка, работа, которую совершает газ, будет равна: 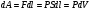 где dV = S dl - изменение объема газа. где dV = S dl - изменение объема газа.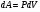 - работа, совершаемая газом при изменении его объема - работа, совершаемая газом при изменении его объемав) Молярная теплоёмкость газа – это количество теплоты, сообщённой 1 молю газа, для увеличения его температуры на dT. 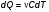 - теплота, сообщённая газу для увеличения его температуры на dT. - теплота, сообщённая газу для увеличения его температуры на dT.Применим первое начало термодинамики к изопроцессам в газе. Изопроцесс - это процесс, происходящий в газе, когда один из параметров, описывающих газ, является постоянным. теплоемкость для случаев, когда нагревание происходит при постоянном объеме или постоянном давлении. Для первого случая теплоемкость обозначается Cv и равна 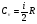 , для второго случая теплоемкость обозначается Cp и равна , для второго случая теплоемкость обозначается Cp и равна 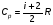 , где i – число степеней свободы молекулы. Для изотермического процесса теплоемкость CТ = , а для адиабатического процесса теплоемкость Cадиаб. = 0. , где i – число степеней свободы молекулы. Для изотермического процесса теплоемкость CТ = , а для адиабатического процесса теплоемкость Cадиаб. = 0. Согласно рассмотренной нами теории теплоемкости Cv и Cp газов должны быть целыми, кратными R/2, ибо число степеней свободы может быть только целым.  15. Термодинамика изохорического процесса: V=const Рассмотрим закон, описывающий этот процесс и его график в координатах (P,V). Этот закон является частным случаем уравнения состояния идеального газа: PV = RT. Закон Шарля: 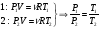 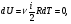 Так как V=const, то dV=0 и dA=PdV=0, т.е 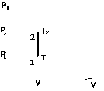 A=0 - работа совершаемая газом при изохорическом процессе равна нулю. Тогда dQ=dU - первое начало термодинамики для изохорического процесса. Поскольку количество теплоты, сообщенное газу, равно dQ=  *CvdT, где *CvdT, где  - молярная теплоёмкость газа при постоянном объёме, то мы получаем полезную формулу для подсчёта приращения внутренней энергии газа: - молярная теплоёмкость газа при постоянном объёме, то мы получаем полезную формулу для подсчёта приращения внутренней энергии газа: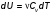 - изменение внутренней энергии газа - изменение внутренней энергии газа Сравнивая эту формулу с другой формулой 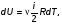 получим выражение для молярной теплоёмкости газа при постоянном объёме: 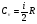 16. Термодинамика изобарического процесса: P=const. Соотношение Майера Сначала рассмотрим закон, описывающий этот процесс и его график в координатах (P,V). 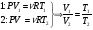 - закон Гей-Люссака. Теперь работа, совершаемая газом, dA=PdV≠0 -приращение внутренней энергии газа тоже не равно нулю dU≠0, и первое начало термодинамики не меняет своего вида:dQ=dU+dA - первое начало термодинамики для изобарического процесса. Формула для подсчёта теплоты теперь примет вид 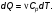 где Cp- молярная теплоёмкость газа при постоянном давлении. где Cp- молярная теплоёмкость газа при постоянном давлении.Приращение внутренней энергии запишем в виде 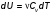 Работa, совершаемую газом: 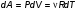 Уравнение Менделеева-Клапейрона 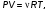 дифференциальное уравнение которого при P=const дает 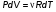 Из выражения для работы следует размерность и физический смысл универсальной газовой постоянной R: 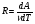 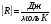 Универсальная газовая постоянная R численно равно работе, совершённой одним молем газа при изобарическом процессе при увеличении его температуры на один градус. Изобарический процесс. Подставляя полученные выражения для dQ, dU, dA в первое начало термодинамики, получим: 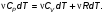 Сократить на dT, получим соотношение между молярными теплоёмкостями газа при постоянном объёме Cv и постоянном давлении Cp: Сократить на dT, получим соотношение между молярными теплоёмкостями газа при постоянном объёме Cv и постоянном давлении Cp: Cp= Cv+R - соотношение Майера. Cv=(i/2)R, получим аналогичное выражение для Cp Cp=((i+2)/2)R Выражение для отношения моляр-х теплоёмкостей Cp и Cv: 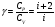 Для двухатомных молекул при невысоких температурах i = 5, тогда γ=1,4. Работа, совершаема газом при изобарическом процессе (P=const): 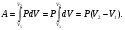 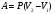
На графике (P,V) работа, совершаемая газом, численно равна площади прямоугольника 1-2-V1-V2, построенного под изобарой 17.Термодинамика изотермического процесса: T=const. Закон, описывающий этот процесс, и его график в координатах (P,V). 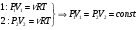 - закон Бойля-Мариотта Так как T = const, то т. е. dU = 0 - изменение внутренней энергии газа при изотермическом процессе равно нулю. Тогда dQ = dA - Первое начало термодинамики при изотермическом процессе При изотермическом процессе вся теплота, сообщенная газу, идет на работу, совершаемую газом: Q = A. Работа, совершаемая газом при изотермическом процессе. Используя уравнение Менделеева-Клапейрона 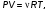 представим элементарную работу в виде: представим элементарную работу в виде: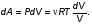 Тогда 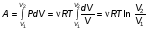 . .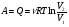 работа, совершаемая газом при изотермическом процессе Учитывая то, что при изотермическом процессе 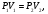 работу можно вычислить также по формуле: работу можно вычислить также по формуле: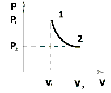  ; ;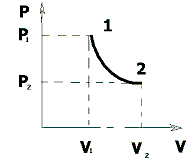 На графике (P,V) работа, совершаемая газом, численно равна площади (1-2-V1-V2) под кривой, описывающий изотермический процесс. 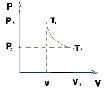 18. Термодинамика адиабатического процесса: dQ=0 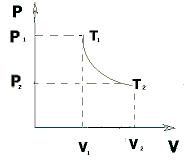 Адиабатическийпроцесс - это процесс, протекающий без теплообмена с окружающей средой. Поскольку dQ = 0, то первое начало термодинамики примет вид:dU+dA=0 Работа, совершаемая газом: 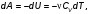 или работа для конечного адиабатического процесса: 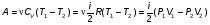 - -Исходя из dU + dA = 0, выведем закон, которому удовлетворяют параметры газа при адиабатическом процессе. Для этого dU и dA представим в виде 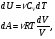 Подставив это выражение в dU + dA = 0, получим дифференциальное уравнение: 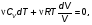 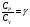 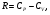 которое, разделив на СV T и используя соотношения  можно записать в виде 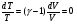 . .Это дифференциальное уравнение приводится к полному дифференциалу: 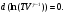 уравнение адиабатического процесса в переменных(T,V): 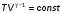 Воспользовавшись уравнением Менделеева-Клапейрона PV = RT, можно перейти к переменным (P,V) и (T,P). Например, из 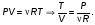 Подставляя это в уравнение Подставляя это в уравнение 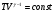 , получим , получим  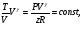 или 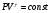 - уравнение Пуассона, где - уравнение Пуассона, где 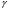 -коэффициент Пуассона. -коэффициент Пуассона.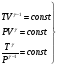 уравнения адиабаты. 19. Политропические процессы – это процессы, при которых тердлёмкость газа =const (c=const) 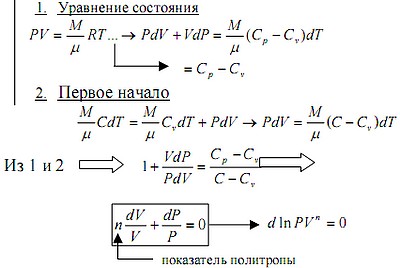  20. 2-е начало термодинамики. Цикл Карно и его КПД Второе начало термодинамики: Невозможно построить периодически действующую тепловую машину, которая бы всю подводимую к ней теплоту превращала в работу, т.е. всегда 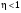 Карно предложил идеальный цикл, который даёт максимальное КПД т.е. 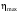 . Этот цикл состоит из двух изотерм и двух адиабат и носит название цикла Карно. . Этот цикл состоит из двух изотерм и двух адиабат и носит название цикла Карно.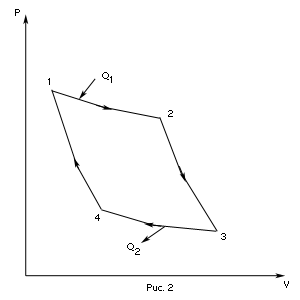 1→2- изотермическое расширение при T1 2→3- адиабатическое расширение, dQ=0 3→4- изотермическое сжатие при T2 4→1- изотермическое сжатие, dQ=0. При изотермическом процессе внутренняя энергия идеального газа остаётся постоянной. Поэтому количество полученной газом теплоты Q1 равно работе A12, совершаемой газом при переходе из состояния 1 в состояние 2. Эта работа равна 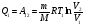 , где m – масса идеального газа в тепловой машине. , где m – масса идеального газа в тепловой машине.Количество отдаваемой холодильнику теплоты Q2 равно работе A34: 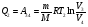 Для того чтобы цикл был замкнутым, состояния 1 и 4, 2 и 3 должны лежать на одной и той же адиабате: 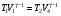 , ,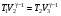 Разделив одно соотношение на другое, приходим к условию замкнутости цикла: V2/V1=V3/V4 Теперь подставляя Q1 и Q2 в выражение для КПД, получим КПД цикла Карно: 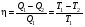 где T1 - температура нагревателя, T2 - температура холодильника. КПД цикла Карно является максимальным КПД из всех возможных циклов, осуществляемых в данных температурных интервалах T1 и T2. где T1 - температура нагревателя, T2 - температура холодильника. КПД цикла Карно является максимальным КПД из всех возможных циклов, осуществляемых в данных температурных интервалах T1 и T2.В общем случае при возможности необратимого цикла Карно это соотношение примет вид: 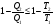 , , 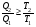 , или , или 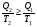 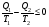 Для обратимого цикла Карно: 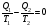 для необратимого цикла Карно: 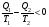 |
