Основные понятия баз данных. Основные понятия баз данных. Субд

Название	Основные понятия баз данных. Субд
Анкор	Основные понятия баз данных
Дата	24.04.2023
Размер	93.41 Kb.
Формат файла
Имя файла	Основные понятия баз данных.docx
Тип	Документы #1087024

Основные понятия баз данных. СУБД.

база данных – это организованная структура, предназначенная для хранения информации. Из такого определения следует, что в базе данных (БД) хранятся не только собственно данные того или иного типа, но и методы (программный код) их обработки. Система управления базой данных (СУБД) – это комплекс программных средств, предназначенных для создания структуры новой базы, наполнения ее содержимым, редактирования содержимого и визуализации информации. Под визуализацией информации базы понимается отбор отображаемых данных в соответствии с заданным критерием, их упорядочение, оформление и последующая выдача на устройство вывода или передача по каналам связи. Системы управления базами данных можно разделить условно на специализированные, созданные для управления конкретной БД, и универсальные, опирающиеся на единый устоявшийся комплекс основных понятий и пригодные для создания и обслуживания разнообразных баз данных

2. Универсальная СУБД MS Access. Основные компоненты. Таблицы, формы, отчеты, запросы.

Универсальной СУБД является программа Microsoft Access, входящая в состав офисного пакета Microsoft Office. Основными объектами базы данных являются взаимосвязанные между собой таблицы. В простейшем случае БД состоит из одной таблицы. Структуру двумерной таблицы образуют столбцы и строки, их аналогами в структуре простейшей базы данных являются поля и записи. Если записей в таблице пока нет, значит, ее структура образована только набором полей. Изменив состав полей базовой таблицы (или их свойства), мы изменяем структуру базы данных и, соответственно, получаем новую базу данных.
• Имя поля – определяет, как следует обращаться к данным этого поля при автоматических операциях с базой (по умолчанию имена полей используются в качестве заголовков столбцов таблиц).
• Тип поля – определяет тип данных, которые могут содержаться в данном поле.
• Размер поля – определяет предельную длину (в символах) данных, которые могут размещаться в данном поле.
• Формат поля – определяет способ форматирования данных в ячейках, принадлежащих полю. • Маска ввода – определяет форму, в которой вводятся данные в поле (средство автоматизации ввода данных).
• Подпись – определяет заголовок столбца таблицы для данного поля (если подпись не указана, то в качестве заголовка столбца используется свойство Имя поля).
• Значение по умолчанию – то значение, которое вводится в ячейки поля автоматически (средство автоматизации ввода данных).
• Условие на значение – ограничение, используемое для проверки правильности ввода данных (средство автоматизации ввода, которое используется, как правило, для данных, имеющих числовой тип, денежный тип или тип даты).
• Сообщение об ошибке – текстовое сообщение, которое выдается автоматически при попытке ввода в поле ошибочных данных (проверка ошибочности выполняется автоматически, если задано свойство Условие на значение).
• Обязательное поле – свойство, определяющее обязательность заполнения данного поля при наполнении базы;
• Пустые строки – свойство, разрешающее ввод пустых строковых данных (от свойства Обязательное поле отличается тем, что относится не ко всем типам данных, а лишь к некоторым, например, к текстовым).
• Индексированное поле – если поле обладает этим свойством, все операции, связанные с поиском или сортировкой записей по значению, хранящемуся в данном поле, существенно ускоряются. Кроме того, для индексированных полей можно сделать так, что значения в записях будут проверяться по этому полю на наличие повторов, что позволяет автоматически исключить дублирование данных

Базы данных СУБД Microsoft Access работают с разнообразными типами данных
• Текстовый – тип данных, используемый для хранения обычного неформатированного текста ограниченного размера (до 255 символов). • Поле Мемо – специальный тип данных для хранения больших объемов текста (до 65 535 символов). Физически текст не хранится в поле. Он хранится в другом месте базы данных, а в поле хранится указатель на него, но для пользователя такое разделение заметно не всегда. 12 • Числовой – тип данных для хранения действительных чисел. • Дата/время – тип данных для хранения календарных дат и текущего времени. • Денежный – тип данных для хранения денежных сумм. Теоретически, для их записи можно было бы пользоваться и полями числового типа, но для денежных сумм есть некоторые особенности (например, связанные с правилами округления), которые делают более удобным использование специального типа данных, а не настройку числового типа. • Счетчик – специальный тип данных для уникальных (не повторяющихся в поле) натуральных чисел с автоматическим наращиванием. Естественное использование – для порядковой нумерации записей. • Логический – тип для хранения логических данных (могут принимать только два значения, например Да или Нет). • Поле объекта OLE – специальный тип данных, предназначенный для хранения объектов OLE, например мультимедийных. Реально, конечно, такие объекты в таблице не хранятся. Как и в случае полей MEMO, они хранятся в другом месте внутренней структуры файла базы данных, а в таблице хранятся только указатели на них (иначе работа с таблицами была бы чрезвычайно замедленной). • Гиперссылка – специальное поле для хранения адресов URL для web-объектов Интернета. При щелчке на ссылке автоматически происходит запуск браузера и воспроизведение объекта в его окне. • Мастер подстановок – это не специальный тип данных. Это объект, настройкой которого можно автоматизировать ввод данных в поле так, чтобы не вводить их вручную, а выбирать из раскрывающегося списка

Таблицы – основные объекты любой базы данных, так как хранят и структуру базы (поля, их типы и свойства) и данные, имеющиеся в базе.
Формы – это средства для ввода и отображения данных, причем, как правило, только одной записи таблицы. Задача формы – предоставить пользователю средства для заполнения только тех полей, которые ему заполнять положено. Одновременно с этим в форме можно разместить специальные элементы управления (счетчики, раскрывающиеся списки, переключатели, флажки и прочие) для автоматизации ввода. Преимущества форм раскрываются особенно наглядно, когда происходит ввод данных с заполненных бланков. В этом случае форму делают графическими средствами так, чтобы она повторяла оформление бланка, – это заметно упрощает работу наборщика, снижает его утомление и предотвращает появление печатных ошибок. С помощью форм данные можно не только вводить, но и отображать. При выводе данных с помощью форм также можно применять специальные средства оформления

Отчеты по своим свойствам и структуре отчеты во многом похожи на формы, но предназначены только для вывода данных 14 принтер. В связи с этим отчеты отличаются тем, что в них приняты специальные меры для группирования выводимых данных и для вывода специальных элементов оформления, характерных для печатных документов (верхний и нижний колонтитулы, номера страниц, служебная информация о времени создания отчета и т. п.)
Запросы служат для извлечения данных из таблиц и предоставления их пользователю в удобном виде. С помощью запросов выполняют такие операции, как отбор данных, их сортировку и фильтрацию. С помощью запросов можно выполнять преобразование данных по заданному алгоритму, создавать новые таблицы, выполнять автоматическое наполнение таблиц данными, импортированными из других источников, выполнять простейшие вычисления в таблицах и многое др.

3. Специализированные информационные ресурсы для автоматизации расчетов в экологии и инженерной защите окружающей среды.
электронные таблицы MS Excel и математический пакет Mathcad. Электронные таблицы Microsoft Excel входят в пакет Microsoft Office и изучаются как в школьном, так и в вузовском курсах информатики. Остановимся здесь только на двух важных возможностях программы, существенных для изучения нашей дисциплины – построении графиков и матричных операциях. Эти вопросы отражены в многочисленной учебной литературе, в том числе базовом учебнике [4], однако обратим внимание на сетевой ресурс [7], который рассматривает вопросы применения возможностей MS Excel в хемометрике – научном направлении, базирующемся на применении математических методов для решения химических и химико-технологических задач. В программе MS Excel используется термин диаграмма для обозначения всех видов графического представления числовых данных. Построение графического изображения производится на основе ряда данных. Так называют группу ячеек с данными в пределах отдельной строки или столбца. На одной диаграмме можно отображать несколько рядов данных. Диаграмма представляет собой вставной объект, внедренный на один из листов рабочей книги. Она может располагаться на том же листе, на котором находятся данные, или на любом другом листе (часто для отображения диаграммы отводят отдельный лист). Диаграмма сохраняет связь с данными, на основе которых она построена, и при обновлении этих данных немедленно изменяет свой вид. Схема построения диаграмм проста: подготавливается таблица с данными для отображения, затем диапазон с данными выделяется и через панель инструментов Вставка (Мастер диаграмм в версиях офисного пакета до 2003 г.) выбирается диаграмма нужного типа. Чаще всего удобно заранее выделить область, содержащую данные для построения диаграммы, но задать эту информацию можно и через контекстное меню диаграммы, вызываемое правой кнопкой мыши (пункт Выбрать данные…). Отметим, что для построения графика в координатах X–Y следует использовать точечную диаграмму. В этом случае в качестве ряда данных для каждой кривой потребуется задать (выде- 16 лить) два столбца – первый – со значением абсцисс, второй – ординат. Построение графиков мы будем использовать для визуального представления результатов решения дифференциальных уравнений – функций, полученных в результате численного интегрирования. Графические возможности MS Excel применимы и для отображения любых других таблично заданных функций, например, результатов экспериментальных исследований, что широко применяют студенты при выполнении выпускных квалификационных работ Вычислительные возможности программы MS Excel существенно расширяются за счет многочисленных встроенных функций, которые можно вызывать через строку функций вручную или выбирать из списков, вызываемых кнопкой fx – Вставить функцию. В рамках рассматриваемой дисциплины представляют интерес матричные операции, реализованные в математическом аппарате электронных таблиц. Операции с матрицами (обращение матриц, умножение, транспонирование и пр.) реализованы через функции. Особенностью инициации функций является специфическая последовательность действий: сначала требуется выделить диапазон ячеек для результата действия функции, затем в строке формул сформировать требуемую функция и, наконец, применить функцию, нажав одновременно клавиши Ctrl/Shift/Enter

4. Основные компоненты банка данных по физико-химическим свойствам веществ и смесей. Использование банка данных в расчетах.

5. MS Excel как средство создания и управления базами данных. Организация фильтрации данных.

С помощью автофилеров или встроенных операторов сравнения, таких как "больше" и "10 лучших" в Excel вы можете показать нужные данные и скрыть остальные. После фильтрации данных в диапазоне ячеек или таблице вы можете повторно использовать фильтр, чтобы получить последние результаты, или очистить фильтр, чтобы повторно отфильтровать все данные.

Используйте фильтры, чтобы временно скрывать некоторые данные в таблице и видеть только те, которые вы хотите.

Фильтрация диапазона данных

Выберите любую ячейку в диапазоне данных.
Выберите Фильтр> данных.
Выберите стрелку в столбце .
Выберите Текстовые фильтры или Числовое фильтры, а затем выберите сравнение, например Между.
Введите условия фильтрации и нажмите кнопку ОК.

Фильтрация данных в таблице

При вводе данных в таблицу в заголовки ее столбцов автоматически добавляются элементы управления фильтрацией.

Выберите стрелку в столбца, который вы хотите отфильтровать.
Сберем (Выберите все) и выберем поля, которые вы хотите отобрать.
Нажмите кнопку ОК.

Стрелка загона столбца

меняется на

фильтра. Щелкните этот значок, чтобы изменить или очистить фильтр.

MS Excel и особенности организации матричных операций.

2. Матричные операции

2.1. Формулы массива

Многие операции с матрицами выполняются с помощью формул специального вида, называемыми формулами массива. От других формул они отличаются тем, что их результатом является не одна величина (число), а набор величин – массив. При вводе таких формул требуется специальное подтверждение – вместо клавиши ENTER надо нажимать комбинацию из трех клавиш CTRL+SHIFT+ENTER.

Поясним использование формул массивов на простом примере. Предположим, что нам нужно выполнить автошкалирование (стандартизацию) данных, записанных в матрице X. Для этого сначала нужно вычислить средние значения m_j и среднеквадратичные отклонения s_j для каждого (j-го) столбца X, а затем вычесть из каждого столбца величину m_j и поделить на величину s_j

Такое преобразование можно сделать с помощью обычных формул

Надо только не забыть указать знак $ перед номерами строк 9 (m) и 11 (s) , чтобы зафиксировать положение соответствующих величин в строках.

Если матрица X велика, то удобнее воспользоваться формулой массива. (Рис. 26). Назовем соответствующие области на листе: X, m и s. Отметим пустую область N3:R7, размеры которой совпадают с ожидаемым результатом. После этого введем в Formula Bar выражение =(X-m)/s. Завершает ввод комбинация клавиш CTRL+SHIFT+ENTER. Если все сделано правильно, то в Formula Bar появится формула { =(X-m)/s}, заключенная в фигурные скобки {}. Это – признак формулы массива. .

2.2. Создание и изменение формул массива

Для того чтобы правильно ввести формулу массива, нужно выделить на листе область, размеры которой совпадают с ожидаемым результатом.

Если выделить слишком большую область, то при вычислении избыточные ячейки будут заполнены символами ошибки #N/A. Если область вывода будет меньше, чем нужно, то часть результатов пропадет. После выделения области, в Formula Bar

записывается формула и нажимается CTRL+SHIFT+ENTER.

Альтернативно, сначала можно ввести формулу в одну ячейку, затем отметить область вывода, начиная с этой ячейки (право и вниз), потом перейти в Formula Bar и нажать CTRL+SHIFT+ENTER.

Для того, чтобы изменить формулу массива нужно выделить область содержащую результат. Затем нужно перейти Formula Bar. При этом фигурные скобки вокруг формулы { } исчезнут. После этого формулу можно изменить и нажать CTRL+SHIFT+ENTER.

Для того чтобы расширить область, которую занимает формула массива, достаточно выделить для нее новую область, перейти в Formula Bar и нажать CTRL+SHIFT+ENTER. А вот для того, чтобы уменьшить эту область (например, чтобы избавиться от символов #N/A) придется потратить больше сил. Сначала нужно встать на любую ячейку области, перейти в Formula Bar и скопировать строку формулы. Затем нужно стереть содержимое старой области и отметить новую, меньшую область. После этого опять перейти в Formula Bar, вставить формулу и нажать CTRL+SHIFT+ENTER.

Изменять отдельные ячейки в формуле массива нельзя. При попытке сделать это появляется предупреждение .

2.3. Простейшие операции с матрицами

С помощью формул массива матрицы можно складывать и умножать на числа.

Для перемножения двух матриц используется функция MMULT

2.4. Доступ к частям матрицы

Для доступа и отделения частей матрицы применяются две стандартные функции листа.

OFFSET / СМЕЩ

Возвращает ссылку на диапазон, отстоящий от ячейки или диапазона ячеек на заданное число строк и столбцов.

Синтаксис

OFFSET(reference, rows, cols [, height] [, width])

reference – это ссылка на область, начиная с которой вычисляется смещение;

rows – число строк, на которое надо сместиться (положительное – вниз, отрицательное вверх от начала);

cols –То же, но для столбцов (положительное – вправо, отрицательное влево от начала);

height – необязательный аргумент. Положительное число строк возвращаемой ссылки;

width – необязательный аргумент. Положительное число столбцов возвращаемой ссылки.

Примечания

Если аргументы height или width опущены, то предполагается, что используется такая же высота или ширина, как в аргументе reference;
Аргумент reference – это ссылка на область, которая должна быть реальным, а не виртуальным массивом, т.е. находиться где-то на листе.

Пример

OFFSET является функцией массива и ее ввод должен завершаться нажатием комбинации CTRL+SHIFT+ENTER.

INDEX / ИНДЕКС

Возвращает значения элементов в массиве, выбранных с помощью индексов строк и столбцов.

Синтаксис

INDEX (reference [, row_num] [, column_num])

reference – это массив значений (матрица);

row_num – необязательный аргумент. Номер строки, из которой берутся значения;

col_num –необязательный аргумент. Номер столбца, из которого берутся значения;

Примечания

Если аргумент row_num опущен, то выбирается весь столбец;
Если аргумент col_num опущен, то выбирается вся строка;
Если указаны оба необязательных аргумента, то возвращается значение, находящееся в ячейке на пересечении соответствующей строки и столбца;
Аргумент reference может быть ссылкой, как на область, так и на виртуальный массив.

Пример

INDEX является функцией массива и ее ввод должен завершаться нажатием комбинации CTRL+SHIFT+ENTER.

2.5. Унарные операции

К матрицам можно применять следующие унарные формулы.

MINVERSE / МОБР

Возвращает обратную матрицу.

Синтаксис

MINVERSE (array)

array – это массив значений (матрица).

Примечания

Матрица array должна быть квадратной;
Если матрица вырождена, то выводится символ ошибки #VALUE!.

Пример

MINVERSE является функцией массива и ее ввод должен завершаться нажатием комбинации CTRL+SHIFT+ENTER.

2.6. Бинарные операции

К матрицам можно применять следующие бинарные операции.

MMULT / МУМНОЖ

Возвращает произведение двух матриц.

Синтаксис

MMULT (array1, array2)

array1, array2 – перемножаемые матрицы.

Примечания

Число столбцов в матрице array1 должно быть равно числу строк в матрицу array2, иначе выводится символ ошибки #VALUE!;
В получаемом массиве должно быть не более 5461 элементов (Excel 2003).

Пример

MMULT является функцией массива и ее ввод должен завершаться нажатием комбинации CTRL+SHIFT+ENTER.

Для построения регрессионных зависимостей используются несколько стандартных функций листа.

TREND / ТЕНДЕНЦИЯ

Строит линейную регрессию

y=b+m₁ x₁+…+m_J x_J+e

Аппроксимирует известные значения вектора откликовknown_y's для заданных значений матрицы предикторов known_x's и возвращает значения y, для заданного массива new_x's.

Синтаксис

TREND(known_y's [,known_x's] [,new_x's] [,const])

known_y's – вектор известных значений откликов y (калибровочный набор);

known_x's – необязательный аргумент. Матрица известных значений предикторов X (калибровочный набор);

new_x's – необязательный аргумент. Матрица новых значений предикторов X_new (проверочный набор) для которых вычисляются и выводятся значения откликов;

const – необязательный аргумент. Логическое значение, которое указывает, требуется ли, чтобы параметр b был равен нулю. Если const имеет значение TRUE или опущено, то b вычисляется обычным образом, иначе b=0.

Примечания

Вектор known_y's должен занимать один столбец, тогда каждый столбец матрицы массива known_x's интерпретируется как отдельная переменная;
Если аргумент known_x's опущен, то предполагается, что это вектор чисел {1;2;3;...} такого же размера, как и known_y's;
Матрица новых значений new_x's должна иметь столько же столбцов (переменных), как и матрица known_x's;
Если аргумент new_x's опущен, то предполагается, что он совпадает с массивом known_x's. Результат является вектором, в котором число строк равно числу строк в массиве new_x's.

Функция TREND является функцией массива и ее ввод должен завершаться нажатием комбинации CTRL+SHIFT+ENTER. ,

LINEST / ЛИНЕЙН

Дополняет функцию TREND и выводит некоторые статистические значения, связанные с регрессией

y=b+m₁ x₁+…+m_J x_J+e

Синтаксис

LINEST(known_y's [,known_x's] [,new_x's] [,const] [,stats])

known_y's – вектор известных значений откликов y (калибровочный набор);

known_x's – необязательный аргумент. Матрица известных значений предикторов X (калибровочный набор);

new_x's – необязательный аргумент. Матрица новых значений предикторов X_new (проверочный набор) для которых вычисляются и выводятся значения откликов;

const – необязательный аргумент. Логическое значение, которое указывает, требуется ли, чтобы параметр b был равен нулю. Если const имеет значение TRUE или опущено, то b вычисляется обычным образом, иначе b=0;

stats – необязательный аргумент. Логическое значение, которое указывает, нужно ли выводить дополнительные статистические значения. Если stats имеет значение FALSE или опущено, то выводятся только оценки коэффициентов m_J, …, m₂, m₁ и b . Иначе выводится целая таблица

m_J, …, m₂, m₁ и b – оценки регрессионных коэффициентов;

s_J, …, s₂, s₁ и s_b – стандартные ошибки для оценок регрессионных коэффициентов;

R² – коэффициент детерминации;

s_y – стандартная ошибка оценки y;

F – F-статистика;

DoF – число степеней свободы;

SS_reg – регрессионная сумма квадратов;

SS_res – остаточная сумма квадратов.

Примечания

LINEST – это очень плохо сконструированная функция, очень неудобная в практическом применении;
Примечания, представленные в описании функции TREND полностью применимы к функции LINEST.

Пример

Функция LINEST является функцией массива и ее ввод должен завершаться нажатием комбинации CTRL+SHIFT+ENTER.

2.9. Виртуальный массив

При анализе данных часто возникает проблема сохранения промежуточных результатов, которые нужны не сами по себе, а только для того, чтобы вычислить по ним другие, полезные значения. Например, остатки в методе PCA часто нам не интересны, а нужны только для определения полной объясненной дисперсии, ортогональных расстояний и т.п. При этом размеры таких промежуточных массивов могут быть очень велики, да и к тому же их приходится вычислять при различных значениях числа главных компонент. Все это ведет к заполнению рабочей книги большим количеством ненужных, промежуточных результатов. Этого можно избежать, если использовать виртуальные массивы. Поясним их суть на простом примере.

Предположим, что задана матрица A, а нужно вычислить детерминант матрицы A^tA . На Рис. 38 показаны два способа вычисления. Первый – через последовательность промежуточных массивов, отмеченных красными стрелками. Второй – с помощью одной формулы, показанной зеленой стрелкой. Оба пути ведут к одному и тому же результату, но красный путь занимает на листе много места, а зеленый последовательно использует несколько промежуточных виртуальных массивов. Все они, по сути, совпадают с реальными массивами красного пути, но на лист не выводятся.

Первый массив – это транспонированная матрица A^t, получаемая как результат функции TRANSPOSE(A).

Второй виртуальный массив получается тогда, когда первый виртуальный массив умножается на матрицу A с помощью функции MMULT(TRANSPOSE(A), A).

И, наконец, к этому, второму виртуальному массиву применяется функция MDETERM.

Виртуальные массивы очень полезны при вычислении всяческих вспомогательных характеристик в анализе многомерных данных: остатков, собственных значений, и т.п. Подробно об этом рассказывается в пособии Расширение возможностей Chemometrics Add-In.

Mathcad как специализированная среда для решения математических задач: обзор основных возможностей.

Основные возможности системы Mathcad:

описание задачи и ее решение в привычном с точки зрения математики виде;
богатый набор встроенных операторов и функций, реализующих разнообразные численные методы решения типовых уравнений и систем;
выполнение операций в символьном виде (вычисление интегралов и производных в аналитической форме, вывод формул для корней уравнений и пр.);
наличие средств для высококачественного оформления документов (близких к программе MS Word);
импорт объектов разного типа для создания иллюстрированных материалов;
интуитивно понятный интерфейс для работы с программным пакетом.

Mathcad. Структура рабочего листа. Типовые блоки и их создание. Привести примеры.

Документ системы Mathcad называют рабочим листом (WorkSheet), и он создается или изменяется в окне редактирования, которое доступно сразу после загрузки программы. Окно редактирования содержит два объекта: курсор в виде красного крестика, определяющего позицию ввода новых компонентов документа, и вертикальную прерывистую черту – границу страницы.

Перемещение курсора производится стрелками на клавиатуре или щелчком мыши в области окна редактирования. Изменить ориентацию и поля страницы можно через пункт меню Файл – Настройка страницы.

Верхнюю часть окна программы занимают панели:

строка заголовка с именем программы и текущего документа;
строка меню, открывающая доступ к подменю с различными камандами;
стандартная панель инструментов;
панель форматирования;
панель инструментов "Математика" (Math) для ввода математических объектов – панель с кнопками, открывающими палитры специальных математических знаков и греческих букв (рис. 1.2).

Отсутствующие на экране панели можно легко восстановить через пункт меню Вид – Панели – Имя панели.

Как уже отмечалось, отличительной особенностью программы Mathcad является возможность описания решаемой задачи в виде, близком к обычной математической записи. Программа не только выполняет вычисления по введенным формулам, решает уравнения различных типов, позволяет легко строить разнообразные графики, но и выполняет преобразования в символическом виде. Встроенные возможности форматирования текста предоставляют средства для оформления документа в стиле программы MS Word.

Для реализации таких богатых возможностей в меню системы появились функции

Вставить – для вставки объектов и их шаблонов, включая графические элементы;
Формат – для изменения формата объектов;
Инструмент – для управления процессом вычислений;
Символика – для выбора операций символьного процессора.

Компоненты документа Mathcad создаются не только вводом символов с клавиатуры, но и с использованием наборов специальных математических символов, размещенных на палитрах панели "Математика".

Операции с блоками

любой блок можно выделить, щелкнув в области этого блока левой кнопкой мыши;
блок можно перетащить мышью в любое место рабочего листа (курсор мыши на границе блока превращается в черную "лапку");
группу блоков можно выделить протягиванием мыши, а затем произвести групповые операции (удалить, переместить, выровнять по горизонтали или вертикали соответствующими кнопками на панели инструментов "Стандартная" и пр.);
размеры текстового блока можно изменить, перетащив за границы за засечки на двух сторонах и правом нижнем углу.

Mathcad. Символьные вычисления. Вычисление интегралов, производных.

С помощью аналитических вычислений находят аналитические или полные решения уравнений и систем, вычисляют в производные и неопределенные интегралы, а также проводят преобразования сложных выражений (например, упрощение). Иначе говоря, при таком подходе можно получить результат в виде некоторой функции. В программе Mathcad при проведении символьных преобразований конкретные значения, присвоенные переменным, игнорируются – переменные рассматриваются как неопределенные параметры.

Для проведения таких символьных операций, как вычисление производной или интеграла можно набрать выражения с помощью панели Исчисление (рис. 1.15) или "горячих" клавиш, описанных в приложении, и затем использовать оператор вычисления в символьном виде "

" панели Символика (рис. 1.16):

Команды для выполнения аналитических вычислений в основном сосредоточены в меню Символика (Symbolics) и продублированы на аналогичной панели инструментов.

Чтобы упростить выражение (или часть выражения), надо выбрать его при помощи уголкового курсора и дать команду Символика > Упростить (Symbolics > Simplify). При этом выполняются арифметические действия, сокращаются общие множители и приводятся подобные члены, применяются тригонометрические тождества, упрощаются выражения с радикалами, а также выражения, содержащие прямую и обратную функции. Некоторые действия по раскрытию скобок и упрощению сложных тригонометрических выражений требуют применения команды Символика > Раскрыть/Расширить (Symbolics > Expand).

В меню Символика (Symbolics) предусмотрен ряд операций, ориентированных на выделенную переменную, использованную в выражении. Например, команда Solve (Решить) ищет корни функции, заданной данным выражением. В примере в аналитической форме получены все корни полинома второй степени: сначала применена команда solve для решения, а затем simplify для упрощения результата:

Другие возможности использования этого меню включают:

аналитическое дифференцирование и интегрирование: Символика > Переменная > Дифференцировать (Symbolics > Variable > Differentiate) и Символика > Переменная > Интегрировать (Symbolics > Variable > Integrate);

пример:
– исходное выражение:

– результат дифференцирования по х:

– результат интегрирования по х:

замена переменной: Символика > Переменная > Подставить (Symbolics > Variable > Substitute) – вместо переменной подставляется содержимое буфера обмена;

пример:
– исходное выражение:

– в буфер обмена скопировано выражение:

– результат замены переменной х: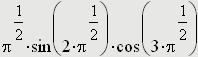

Механизм аналитических вычислений можно использовать для аналитического решения уравнений и систем уравнений и неравенств. Для этого задается блок решения Given, в который помещаются уравния и неравенства, а последняя формула блока должна выглядеть как

Find(х,у,...) ,

где в скобках приведен список искомых величин, а далее следует знак аналитического вычисления, отображаемый в виде стрелки, направленной вправо:

пример:
– начало блока:

– решаемое уравнение:

– поиск решения по х:

Отметим, что функция Find пытается найти решение в аналитической форме. В том случае, если до блока Given задать численно значения всех параметров, входящих в уравнения, а также начальные приближения для корней, то получим решение в числовом виде.

Примеры использования функции Find для решения уравнений и систем уравнений различного типа приведены в соответствующих разделах пособия.

Mathcad. Основные операторы и их использование.
Программные операторы в Mathcad
В системе Mathcad можно реализовать расчеты по сложным разветвленным алгоритмам или с циклическими процессами. Это реализуется использованием встроенных программных операторов, похожих на используемые в различных языках программирования (рис. 1.17). Как видно на рис. 1.18 и 1.19, где вычисляется факториал, программный модуль в системе Malhcad превратился в самостоятельный блок, причем при необходимости выполнить несколько операторов, их объединяют жирной вертикальной чертой.

Модуль может вести себя как безымянная функция без параметров, но возвращающая результат – первый пример. Программный модуль может выполнять и роль тела функции пользователя с именем и параметрами – второй пример.

Набор программных операторов для создания программных модулей ограничен и содержит следующие элементы:

Add Line – создает и при необходимости расширяет жирную вертикальную линию, справа от которой в шаблонах задается запись программного блока;
– символ локального присваивания (в теле модуля);
if – условный оператор;
for – оператор задания цикла с фиксированным числом повторений;
while – оператор задания цикла, действующего до тех пор, пока выполняется некоторое условие;
otherwise – оператор иного выбора (обычно применяется с if);
break – оператор прерывания;
continue – оператор продолжения;
return – оператор возврата;
on error – оператор обработки ошибок.

Оператор добавления линии Add Line выполняет функции расширения программного блока. Расширение фиксируется удлинением вертикальной черты программных блоков или их древовидным расширением. Благодаря этому, в принципе, можно создавать сколь угодно большие программы.

Оператор внутреннего присваивания

выполняет функции внутреннего, локального присваивания. Например, выражение

присваивает переменной x значение 123. Локальный характер присваивания означает, что такое значение х сохраняет только в теле программы. За пределами тела программы значение переменной х может быть неопределенным, либо равно значению, которое задается вне программного блока операторами локального := или глобального присваивания.

Условный оператор if является оператором для создания условных выражений. Он задается в виде:

Если условие выполняется, то возвращается значение выражения. Совместно с этим оператором часто используются операторы прерывания break и иного выбора otherwise.

Оператор цикла for служит для организации циклов с заданным числом повторений. Он записывается в виде: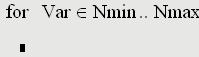

Эта запись означает, что выражение, помешенное в расположенный ниже заменитель, будет выполняться для значений переменной Var, меняющихся от Nmin до Nmax с шагом +1. Переменную счетчика Var можно использовать в исполняемом выражении.

Оператор цикла while служит для организации циклов, действующих до тех пор, пока выполняется некоторое условие. Этот оператор записывается в виде: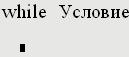

Выполняемое выражение записывается на место расположенного ниже заполнителя.

Оператор иного выбора otherwise обычно используется совместно с оператором if. Это поясняет следующая программная конструкция: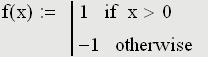

Здесь f(x) получает значение 1, если х>0, и –1 во всех остальных случаях.

Оператор прерывания break вызывает прерывание работы программы всякий раз, как он встречается. Чаще всего он используется совместно с оператором условного выражения if и операторами циклов while и for, обеспечивая переход в конец тела цикла.

Оператор продолжения continue используется для продолжения работы после прерывания программы. Он также чаще всего используется совместно с операторами задания циклов while и for, обеспечивая возвращение в точку прерывания и продолжение вычислений.

Оператор возвращения return прерывает выполнение программы и возвращает значение операнда, стоящего следом за ним. Например, конструкция

будет возвращать значение 0 при любом х < 0.

Оператор и функция обработки ошибок позволяет создавать конструкции обработчиков ошибок. Этот оператор задается в виде:

Здесь если при выполнении Выражения_1 возникает ошибка, то выполняется Выражение_2. Для обработки ошибок полезна также функция error(S), которая, будучи помешенной в программный модуль, при возникновении ошибки выводит всплывающую подсказку с надписью, хранящейся в символьной переменной S.

Программный модуль, в сущности, является функцией, но описанной с применением упомянутых программных средств. Она возвращает значение, определяемое последним оператором (если не предусмотрено иное с помощью оператора return). Это значит, что после такого модуля, выделенного как целый блок, можно поставить знак равенства для вывода результата его работы (см. рис. 1.18). В блоке могут содержаться любые операторы и функции входного языка системы. Для передачи в блок значений переменных можно использовать переменные документа, которые ведут себя в блоке как глобальные переменные.

Обычно модулю присваивается имя со списком переменных, после которого идет знак присваивания:=. Переменные в списке являются локальными и им можно присваивать значения при вызове функции, заданной модулем. Локальный характер таких переменных позволяет использовать для их идентификаторов те же имена, что и у глобальных переменных документа. Однако лучше этого не делать и использовать разные имена для локальных переменных программных модулей и переменных документа.

11. Mathcad. Представление данных в виде графиков разного типа.

Для создания графиков в системе MathCAD имеется программный графический процессор. Основное внимание при его разработке было уделено обеспечению простоты задания графиков и их модификации с помощью соответствующих опций. Процессор позволяет строить самые разные графики, например в декартовой и полярной системах координат, трехмерные поверхности, графики уровней и т д

Для построения графиков используются шаблоны Их перечень содержит подменю Graph (Графика) в позиции Insert (Включение) главного меню Большинство параметров графического процессора, необходимых для построения графиков, по умолчанию задается автоматически Поэтому для начального построения графика того или иного вида достаточно задать тип графика В подменю Graph содержится список из семи основных типов графиков. Они позволяют выполнить следующие действия X-Y Plot® (Декартов — создать шаблон двумерного графика график) в декартовой системе координат,

Polar Plot [Ctrl+ 7] — создать шаблон графика в полярной системе (Полярный график) координат, Surface Plot [Ctrl+ 2] — создать шаблон для построения трехмерного (График поверхности) графика, Contour Plot [Ctrl+ 5] — создать шаблон для контурного графика (Карта линий уровня) трехмерной поверхности, 3D Scatter Plot создать шаблон для графика в виде точек (Точечный график) (фигур) в трехмерном пространстве, 3D Bar Chart (Трехмерная создать шаблон для изображения в виде гистограмма) совокупности столбиков в трехмерном про странстве, Vector Field Plot — создать шаблон для графика векторного (Векторное поле) поля на плоскости

Вид окна системы с подменю Insert Graph показан на рис 5. 1. В этом подменю видны команды создания шаблонов указанных выше типов графиков В окне редактирования показаны также два одинаковых графика, но в разных местах и разного размера

Общее понятие о численных методах решения уравнений и систем уравнений, приближенный характер результата решения.

https://portal.tpu.ru/SHARED/b/BGA/bio/bachelors/Tab/Numerica_meth_eq_solution.pdf

13. Системы линейных алгебраических уравнений. Запись системы в стандартной форме. Матричное представление системы.

14. Численные методы решения систем линейных алгебраических уравнений.

15. Решение системы линейных алгебраических уравнений в матричной форме в Mathcad и MS Excel.

16. Понятие корня нелинейного алгебраического уравнения. Отличие точного решения и решения, полученного численным методом. Запись нелинейного алгебраического уравнения в стандартной форме. 8

17. Решение нелинейного алгебраического уравнений. Метод деления отрезка пополам.

18. Итерационные методы решения нелинейного алгебраического уравнений. Методы Ньютона, секущих, итераций. Условия сходимости методов.

19. Решение нелинейных алгебраических уравнений в MS Excel методом подбора параметров.

20. Методы решения систем нелинейных алгебраических уравнений.

21. Матричное представление системы нелинейных алгебраических уравнений. Решение подобных систем в Mathcad.

22. Решение дифференциального уравнения и системы таких уравнений. Форма представления результата численного решения системы дифференциальных уравнений.

23. Численные методы решения систем дифференциальных уравнений: сущность методов и сравнений точности решения. Реализация в Mathcad.

24. Численные методы решения систем дифференциальных уравнений: сущность методов и сравнений точности решения. Реализация в MS Excel.

25. Интегрирование функций: численные методы. Возможность получения аналитического результата в системе символьных вычислений Mathcad.