экзаменагро. Основные понятия линейной алгебры, 1 Дана матрица. Тогда ее размерность равна
 Скачать 1.06 Mb. Скачать 1.06 Mb.
|
)  5. Математическое ожидание нормально распределенной случайной величины 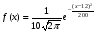 равно … равно …Ответ: 12 6. Дисперсия случайной величины 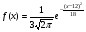 равна … равна …Ответ: 9 7. Плотность вероятности случайной величины Х, подчиненной нормальному закону распределения, задана функцией 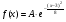 . Тогда коэффициент А равен … . Тогда коэффициент А равен …+1) 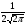 ; ;2) 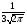 ; ;3) 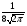 ; ;4) 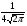 . .8. Непрерывная случайная величина задана плотностью вероятностей 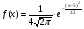 . Тогда произведение . Тогда произведение 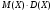 равно … равно …Ответ: 80 9. Диапазон изменения нормально распределенной случайной величины 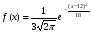 равен … равен …1) 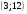 ; ;+2) 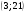 ; ;3) 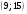 ; ;4) 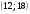 . .10. Интервал, в который значения нормально распределенной случайной величины с вероятностью 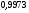 , если математическое ожидание , если математическое ожидание 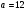 и средним квадратическим отклонением и средним квадратическим отклонением 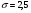 , равен … , равен …1) 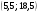 ; ;+2) 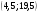 ; ;3) 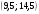 ; ;4) 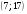 . .[Вероятность попадания в заданный интервал, 1] 1. Масса яблока, средняя величина которой равна 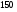 г, является нормально распределенной случайной величиной со средним квадратическим отклонением г, является нормально распределенной случайной величиной со средним квадратическим отклонением 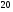 г. Тогда вероятность того, что масса наугад взятого яблока будет заключена в пределах от г. Тогда вероятность того, что масса наугад взятого яблока будет заключена в пределах от 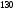 г до г до 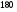 г., равна… г., равна…+1) 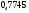 ; ;2) 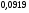 ; ;3) 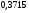 ; ;4) 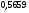 . .2. Средняя глубина заделки семян 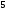 см., среднее квадратическое отклонение равно см., среднее квадратическое отклонение равно 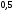 см. Считая глубину заделки семян случайной величиной, распределенной нормально, доля семян посеянных на глубину более см. Считая глубину заделки семян случайной величиной, распределенной нормально, доля семян посеянных на глубину более 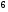 см. равна… см. равна…+1) 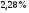 ; ;2) 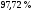 ; ;3) 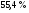 ; ;4) 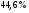 . .3. Случайная величина Х распределена по нормальному закону с 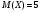 и и 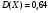 . Вероятность того, что в результате испытания Х примет значение в интервале . Вероятность того, что в результате испытания Х примет значение в интервале 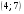 равна … равна …1) 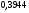 ; ;2) 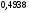 ; ;+3) 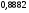 ; ;4) 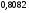 . .4. Случайная величина Х распределена по нормальному закону с 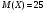 и и 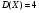 . Вероятность того, что в результате испытания Х примет значение в интервале . Вероятность того, что в результате испытания Х примет значение в интервале 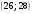 равна … равна …1) 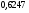 ; ;2) 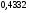 ; ;3) 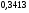 ; ;+4) 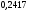 . .5. Для нормально распределенной случайной величины математическое ожидание равно 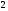 , а среднее квадратическое отклонение , а среднее квадратическое отклонение 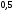 . Вероятность того, что случайная величина примет значение в интервале . Вероятность того, что случайная величина примет значение в интервале 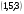 равна… равна…1) 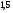 ; ;+2) 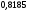 ; ;3) 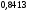 ; ;4) 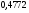 . .6. Вероятность попадания нормально распределенной случайной величины в интервал 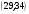 с с 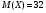 и и 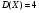 равна … равна …1) 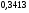 ; ;2) 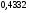 ; ;+3) 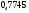 ; ;4) 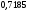 . .7. Интервал, в который значения нормально распределенной случайной величины попадают с вероятностью 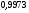 , равен , равен 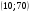 . Тогда среднее квадратическое отклонение случайной величины равно … . Тогда среднее квадратическое отклонение случайной величины равно …+1) 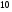 ; ;2) 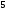 ; ;3) 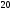 ; ;4) 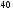 . .8. Средний диаметр стволов деревьев на некотором участке равен 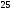 см, среднее квадратическое отклонение равно см, среднее квадратическое отклонение равно 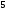 см (диаметр ствола – нормально распределенная случайная величина). Тогда процент деревьев, имеющих диаметр свыше см (диаметр ствола – нормально распределенная случайная величина). Тогда процент деревьев, имеющих диаметр свыше 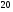 см, равен … см, равен …1) 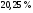 ; ;2) 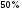 ; ;3) 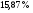 ; ;+4) 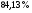 . .9. Среднее квадратическое отклонение нормально распределенной случайной величины равно 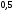 . Тогда вероятность того, что отклонение случайной величины от ее математического ожидания по абсолютной величине не превосходит . Тогда вероятность того, что отклонение случайной величины от ее математического ожидания по абсолютной величине не превосходит 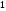 , равна … , равна …1) 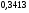 ; ;2) 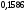 ; ;+3) 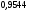 ; ;4) 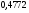 . .10. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины 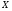 соответственно равны соответственно равны 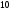 и и 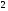 . Тогда вероятность того, что в результате испытания . Тогда вероятность того, что в результате испытания 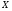 примет значение, заключенное в интервале примет значение, заключенное в интервале 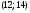 , равна … , равна …1) 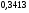 ; ;+2) 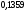 ; ;3) 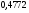 ; ;4) 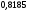 . .[Статистика, 1] 167. Из генеральной совокупности извлечена выборка объема n=50: 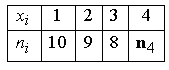 . Тогда n4 равен… . Тогда n4 равен…+ 1) 23 2) 50 3) 24 4) 7 5) 2 168. Получены следующие данные: 5, 4, 8, 4, 9, 5, 7, 4, 5, 7. Тогда частота варианты 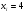 в выборке равна … в выборке равна …ОТВЕТ: 3 169. Получены следующие данные: 5, 4, 8, 4, 9, 5, 7, 4, 5, 7. Тогда частота варианты 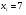 в выборке равна … в выборке равна …ОТВЕТ: 2 170. Получены следующие данные: 5, 4, 8, 4, 5, 5, 7, 4, 5, 7. Тогда частота варианты 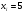 в выборке равна … в выборке равна …ОТВЕТ: 4 171. Из генеральной совокупности извлечена выборка, статистическое распределение которой имеет вид  . Тогда относительная частота варианты . Тогда относительная частота варианты 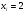 в выборке равна … в выборке равна …1) 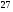 ; ;2) 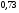 ; ;+3) 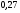 ; ;4) 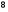 . .5) нет правильного ответа 172. По выборке объема 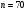 построен полигон частот построен полигон частот  . Тогда частота варианты . Тогда частота варианты 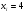 в выборке равна … в выборке равна …ОТВЕТ: 20 173. Из генеральной совокупности извлечена выборка, статистическое распределение которой имеет вид:  . Тогда объем выборки равен … . Тогда объем выборки равен …ОТВЕТ: 35 174. Из генеральной совокупности извлечена выборка, статистическое распределение которой имеет вид  . Тогда объем выборки равен … . Тогда объем выборки равен …ОТВЕТ: 100 175. Из генеральной совокупности извлечена выборка объема 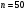 , статистическое распределение которой имеет вид: , статистическое распределение которой имеет вид:  . Тогда число вариант . Тогда число вариант 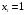 в выборке равно … в выборке равно …ОТВЕТ: 5 176. Из генеральной совокупности извлечена выборка, статистическое распределение которой имеет вид:  . Тогда объем выборки равен … . Тогда объем выборки равен …ОТВЕТ: 50 177. Из генеральной совокупности извлечена выборка объема 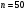 , статистическое распределение которой имеет вид , статистическое распределение которой имеет вид  . Тогда частота варианты . Тогда частота варианты 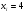 в выборке равна … в выборке равна …ОТВЕТ: 15 1. Из генеральной совокупности извлечена выборка объема 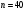 , статистическое распределение которой имеет вид: , статистическое распределение которой имеет вид: 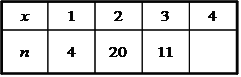 . Тогда число вариант . Тогда число вариант 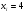 в выборке равно … в выборке равно …Ответ: 5 2. Из генеральной совокупности извлечена выборка, статистическое распределение которой имеет вид:  . Тогда объем выборки равен … . Тогда объем выборки равен …Ответ: 120 3. Получены следующие данные: 5, 7, 8, 4, 5, 5, 7, 8, 5, 7. Тогда относительная частота варианты 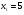 в выборке равна … в выборке равна …1) 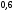 ; ;2) 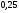 ; ;3) 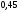 ; ;+4) 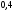 . .4. Из генеральной совокупности извлечена выборка объема 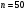 , статистическое распределение которой имеет вид: , статистическое распределение которой имеет вид:  . Тогда число вариант . Тогда число вариант 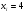 в выборке равно … в выборке равно …1) 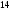 ; ;2) 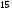 ; ;+3) 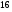 ; ;4) 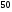 . .5. Получены следующие данные: 5, 4, 8, 4, 9, 5, 7, 4, 5, 7. Тогда частота варианты 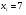 в выборке равна … в выборке равна …1) 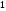 ; ;+2) 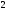 ; ;3) 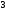 ; ;4) 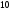 . .6. Из генеральной совокупности извлечена выборка, статистическое распределение которой имеет вид:  . Тогда относительная частота варианты . Тогда относительная частота варианты 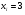 в выборке равна … в выборке равна …1) 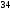 ; ;2) 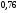 ; ;+3) 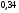 ; ;4) 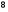 . .7. Из генеральной совокупности извлечена выборка объема 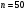 , статистическое распределение которой имеет вид: , статистическое распределение которой имеет вид:  . Тогда относительная частота варианты . Тогда относительная частота варианты 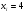 в выборке равна … в выборке равна …1) 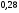 ; ;+2) 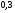 ; ;3) 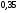 ; ;4) 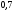 . .8. Получены следующие данные: 5, 7, 8, 4, 5, 5, 7, 8, 5, 7. Тогда относительная частота варианты 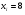 в выборке равна … в выборке равна …1) 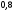 ; ;+2) 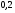 ; ;3) 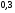 ; ;4) 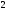 . .9. По выборке объема 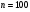 задана таблица задана таблица  . Тогда . Тогда 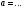 1) 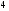 ; ;2) 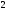 ; ;+3) 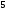 ; ;4)  . .10. По выборке построена гистограмма частот 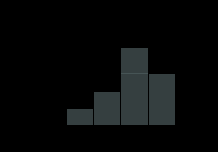 . Тогда объем выборки равен … . Тогда объем выборки равен …Ответ: 64 [Точечные оценки параметров распределения, 1] 1. Медиана вариационного ряда 15, 17, 20, 29, 39, 40, 41 равна … Ответ : 29 2. Признак Х принимал следующие значения: 24, 38, 29, 30, 33, 23, 27, 26, 29, 34. Тогда величина 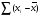 равна … равна …Ответ: 0 3. Мода ряда 5, 7, 8, 4, 5, 5, 7, 8, 5, 7 равна … Ответ: 5 4. Из генеральной совокупности извлечена выборка, статистическое распределение которой имеет вид:  . Тогда выборочная средняя приближенно равна … . Тогда выборочная средняя приближенно равна …1) 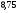 ; ;2) 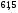 ; ;+3) 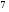 ; ;4) 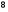 . .5. Медиана вариационного ряда 3, 5, 8, 10, 19, 21, 23, 28 равна … 1) 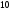 ; ;2) 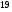 ; ;+3) 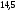 ; ;4) 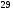 . .6. Проведено шесть измерений некоторой случайной величины: 2, 5, 6, 8, 9, 12. Тогда несмещенная оценка дисперсии равна … 1) 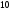 ; ;2) 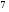 ; ;+3) 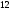 ; ;4) 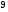 . .7. Из генеральной совокупности извлечена выборка: 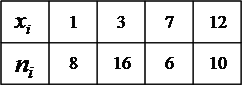 . Тогда выборочная средняя равна … . Тогда выборочная средняя равна …+1) 5,45; 2) 5,75; 3) 6,5; 4) 5,5; 5) 3,5. 8. По выборке объема 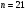 найдена найдена 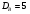 . Тогда несмещенная оценка генеральной дисперсии равна … . Тогда несмещенная оценка генеральной дисперсии равна …1) 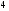 ; ;2) |
