экзаменагро. Основные понятия линейной алгебры, 1 Дана матрица. Тогда ее размерность равна
 Скачать 1.06 Mb. Скачать 1.06 Mb.
|
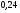 ; ;3) 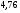 ; ;+4) 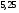 . .9. Производилось обследование хозяйств по числу бригад, работающих на коллективном подряде. Получен следующий ряд распределения: 1,1,1,2,2,3,3,3,3,4,4,5,5,5,6. Модальное значение признака в данном распределении … 1) 3,5; 2) 6; 3) 1; 4) мода отсутствует; +5) 3. 10. Проведено пять измерений некоторой случайной величины: 2, 3, 5, 7, 10. Тогда несмещенная оценка математического ожидания равна … Ответ: 5 [Элементы корреляционного анализа, 1] 1. Известно, что 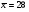 , , 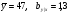 . Тогда уравнение прямой регрессии имеет вид … . Тогда уравнение прямой регрессии имеет вид …+1) 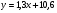 ; ;2) 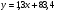 ; ;3) 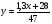 ; ;4) 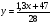 . .2. По расчетам выборочный коэффициент корреляции между двумя признаками равен 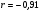 . Тогда можно сделать вывод о том, что … . Тогда можно сделать вывод о том, что …1) расчеты неверны; +2) между величинами существует тесная линейная корреляция; 3) между величинами наблюдается слабая линейная корреляция; 4) между величинами отсутствует линейная корреляция. 3. Известно, что 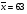 ; ; 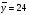 ; ;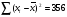 ; ; 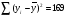 ; ; 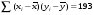 . Тогда коэффициент регрессии У на Х равен … . Тогда коэффициент регрессии У на Х равен …Ответ: 0,54 4. По расчетам выборочный коэффициент корреляции между двумя признаками равен 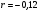 . Тогда можно сделать вывод о том, что … . Тогда можно сделать вывод о том, что …1) расчеты неверны; 2) между величинами существует тесная линейная корреляция; +3) между величинами наблюдается слабая линейная корреляция; 4) между величинами отсутствует линейная корреляция. 5. Известно, что 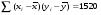 ; ; 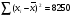 ; ; 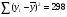 ; ; 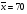 ; ; 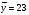 . Тогда уравнение прямой регрессии имеет вид … . Тогда уравнение прямой регрессии имеет вид … 1) 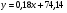 ; ;2) 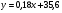 ; ;3) 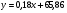 ; ;+4) 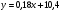 . .6. Уравнение прямой регрессии имеет вид 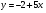 . Тогда выборочный коэффициент корреляции может быть равен … . Тогда выборочный коэффициент корреляции может быть равен …1) 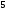 ; ;2) 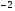 ; ;+3) 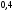 ; ;4) 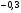 . .7. Уравнение прямой регрессии имеет вид 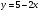 . Тогда выборочный коэффициент корреляции может быть равен … . Тогда выборочный коэффициент корреляции может быть равен …1) 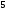 ; ;2) 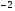 ; ;3) 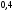 ; ;+4) 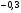 . .8. Известно, что 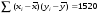 ; ; 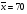 ; ; 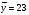 ; ; 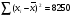 ; ; 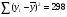 . Тогда выборочный коэффициент корреляции равен … . Тогда выборочный коэффициент корреляции равен …Ответ:0,97. 10. По расчетам выборочный коэффициент корреляции равен 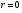 . Тогда можно сделать вывод о том, что … . Тогда можно сделать вывод о том, что …1) расчеты неверны; 2) между величинами существует тесная линейная корреляция; 3) между величинами наблюдается слабая линейная корреляция; +4) между величинами отсутствует линейная корреляция. [Интервальные оценки параметров распределения, 1] 1. Точечная оценка математического ожидания нормального распределения равна 10.Тогда его интервальная оценка может иметь вид … 1) (8,5;10); +2) (8,5;11,5); 3) (8,5;9,5); 4) (10;13); 5) другой вариант ответа. 2. По выборке объема 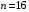 из генеральной совокупности определены из генеральной совокупности определены 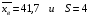 . Тогда 95% доверительный интервал для генеральной средней имеет вид . Тогда 95% доверительный интервал для генеральной средней имеет вид 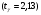 … …1) (25,7;55,7); 2) (41,45;41,95); 3) (37,7;45,7); +4) (39,57;43,83); 5) другой вариант ответа. 3. Если генеральное среднее квадратическое отклонение 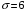 , выборочная средняя , выборочная средняя 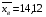 и объем выборки и объем выборки 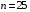 , то доверительный интервал неизвестного математического ожидания , то доверительный интервал неизвестного математического ожидания 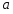 нормально распределенного признака Х генеральной совокупности с надежностью 0,99 равен … нормально распределенного признака Х генеральной совокупности с надежностью 0,99 равен …+1) (11,024;17,216); 2) (10,734;17,476); 3) (11,97;16,27); 4) (11,216; 17,024); 5) другой вариант ответа. 4. В выборке из 20 зерен пшеницы среднее квадратическое отклонение массы зерна составило 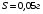 . Предполагая, что случайная величина Х-масса зерна- имеет нормальное распределение с надежностью 0,99, тогда доверительный интервал для неизвестного среднего квадратического отклонения равен … . Предполагая, что случайная величина Х-масса зерна- имеет нормальное распределение с надежностью 0,99, тогда доверительный интервал для неизвестного среднего квадратического отклонения равен …1) (0;0,079); 2) (0,021;1); 3) (0;1) +4) (0,021;0,079); 5) другой вариант ответа. 5. Генеральное среднее квадратическое отклонение 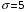 , выборочная средняя , выборочная средняя 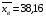 и объем и объем 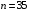 . С надежностью 0,99 доверительный интервал для оценки неизвестного математического ожидания . С надежностью 0,99 доверительный интервал для оценки неизвестного математического ожидания 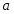 нормально распределенного признака Х генеральной совокупности равен … нормально распределенного признака Х генеральной совокупности равен …1) (36,01;40,31); +2)(35,98;40,34); 3) (35,861;40,459); 4) (10,734;17,476); 5) другой вариант ответа. 6. В выборке из 16 зерен ржи среднее квадратическое массы зерна составило 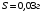 . Предполагая, что случайная величина Х -массы зерна- имеет нормальное распределение с надежностью 0,95, тогда доверительный интервал для неизвестного среднего квадратического отклонения равен … . Предполагая, что случайная величина Х -массы зерна- имеет нормальное распределение с надежностью 0,95, тогда доверительный интервал для неизвестного среднего квадратического отклонения равен …1) (0;0,0432); 2) (0,0134;0,0452); +3) (0,0168;0,0432); 4) (0,021;0,079); 5) другой вариант ответа. |
