экзаменагро. Основные понятия линейной алгебры, 1 Дана матрица. Тогда ее размерность равна
 Скачать 1.06 Mb. Скачать 1.06 Mb.
|
|
6. Эффективность вакцины составляет 80%. Сколько отобрали животных, если приобрели иммунитет 160 животных? 1) 100; +2) 200; 3) 80; 4) 160 5) другой вариант ответа 7. Известно, что всхожесть пшеницы составляет 90%. Сколько взяли зерен, если взошло 360 растений? +1) 400; 2) 200; 3) 90; 4) 360 5) другой вариант ответа 8. Бросают игральную кость. Вероятность того, что выпадет число 5 равна… 1) 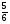 +2) 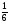 3) 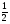 4) 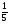 5) другой вариант ответа 9. В группе 13 юношей и 7 девушек. Вероятность того, что для дежурства будет отобрана одна девушка равна… +1) 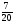 2) 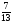 3) 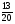 4) 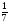 5) другой вариант ответа 10. В корзине 27 саженцев двух сортов, из них 12 сорта А, остальные сорта В. Выбирают один саженец. Вероятность появления саженца сорта В равна… 1) 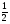 2) 1 3) 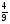 +4) 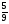 5) другой вариант ответа 1. Вероятность того, что некоторое событие произойдет ровно 2 раза в 3000 испытаниях, если вероятность появления события в одном испытании равна 0,001, находится по … 1) Формуле Бернулли; 2) Локальной теореме Лапласа; +3) Формуле Пуассона; 4) классическому определению вероятности. 2. По какой формуле находится вероятность того, что некоторое событие произойдет ровно 60 раз в 100 испытаниях, если вероятность появления события в одном испытании равна 0,7? 1) Формула Бернулли; +2) Локальная теорема Лапласа; 3) Формула Пуассона; 4) Интегральная теорема Лапласа. 3. По какой формуле находится вероятность того, что некоторое событие произойдет ровно 4 раза в 10 испытаниях, если вероятность появления события в одном испытании равна 0,03. +1) Формула Бернулли; 2) Локальная теорема Лапласа; 3) Формула Пуассона; 4) Интегральная теорема Лапласа. 4. В двух корзинах находятся яблоки. В первой 20 штук, из них 5 поврежденных, во второй 30 штук, из них 6 поврежденных. Наудачу выбранное яблоко оказалось поврежденным. По какой формуле находится вероятность того, что выбранное яблоко взято из первой корзины? 1) по формуле полной вероятности; +2) по формуле Байеса; 3) по интегральной теореме Лапласа; 4) по классическому определению вероятности. 5. Вероятность появления некоторого события в одном испытании равна 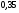 . Тогда вероятность того, что в 10 испытаниях событие наступит ровно . Тогда вероятность того, что в 10 испытаниях событие наступит ровно 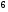 раз, находится по … раз, находится по …+1) формуле Бернулли; 2) формуле Пуассона; 3) локальной теореме Лапласа; 4) интегральной теореме Лапласа. 6. Вероятность появления некоторого события в одном испытании равна 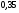 . Тогда вероятность того, что в 20 испытаниях событие наступит ровно . Тогда вероятность того, что в 20 испытаниях событие наступит ровно 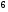 раз, находится по … раз, находится по …1) формуле Бернулли; 2) формуле Пуассона; +3) локальной теореме Лапласа; 4) интегральной теореме Лапласа. 7. В двух корзинах находятся яблоки. В первой 40 штук, из них 9 поврежденных, во второй 50 штук, из них 4 поврежденных. Наудачу из выбранной корзины взяли одно яблоко. По какой формуле находится вероятность того, что выбранное яблоко будет не повреждено? +1) по формуле полной вероятности; 2) по формуле Бернулли; 3) по интегральной теореме Лапласа; 4) по классическому определению вероятности. [Теоремы сложения и умножения вероятностей, 1] 1. От автовокзала отправились два автобуса. Вероятности своевременного прибытия автобуса в пункт назначения соответственно равны: для первого автобуса-0,8, для второго-0,85. Вероятность того, что только один автобус прибудет вовремя, равна… 1) 0,68 +2) 0,29 3) 0,32 4) 0,71 5) другой вариант ответа 2. При подготовке к экзамену один студент выучил 75% материала, а другой-92%. Вероятность того, что экзамен сдаст только один студент, равна… 1) 0,69 2) 0,75 3) 0,92 +4) 0,29 5) другой вариант ответа 3. Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сработает первый сигнализатор, равна 0,9; для второго-0,85. Тогда вероятность того, что при аварии сработает только один, равна… +1) 0,22 2) 0,765 3) 0,235 4) 0,2175 5) другой вариант ответа 4. Стрелок стреляет по мишени, разделенной на три области. Вероятность попадания в первую область равна 0,55; во вторую-0,25. Тогда вероятность того, что стрелок попадет либо в первую, либо во вторую область равна… 1) 0,1375 2) 0,3 +3) 0,8 4) 0,8625 5) другой вариант ответа 5. Вероятность того, что студент сдаст первый экзамен, равна 0,9; второй-0,8; третий-0,7. Тогда вероятность того, что студентом будет сдан только второй экзамен, равна… 1) 0,398 +2) 0,024 3) 0,8 4) 0,3 5) другой вариант ответа 6. Три стрелка независимо друг от друга стреляют по одной цели. Вероятность попадания первого стрелка-0,7; второго-0,8; третьего-0,9. Тогда вероятность того, что в цель попадут только два стрелка, равна… 1) 0,056 +2) 0,398 3) 0,126 4) 0,504 5) другой вариант ответа 7. Вероятность правильного оформления счета на агрофирме составляет 0,95. Во время аудиторской проверки были взяты два счета. Тогда вероятность того, что только один из них оформлен правильно, равна… 1) 0,95 2) 0,475 +3) 0,095 4) 0,0475 5) другой вариант ответа 8. Вероятность получить высокие дивиденды по акциям на первом предприятии-0,2; на втором-0,35. Тогда вероятность того, что акционер, имеющий акции этих предприятий, получит высокие дивиденды только на одном предприятии, равна… 1) 0,07 2) 0,55 3) 0,13 +4) 0,41 5) другой вариант ответа 9. Отдел технического контроля проверяет изделие на стандартность. Вероятность того, что наугад взятое изделие окажется бракованным, равна 0,15. Проверено два изделия. Тогда вероятность того, что одно из них бракованное, равна… +1) 0,255 2) 0,1275 3) 0,8725 4) 0,745 5) другой вариант ответа 10. Коэффициент использования рабочего времени у трех комбайнов соответственно равен 0,85; 0,90 и 0,80. Остановки в работе каждого комбайна случайны и независимы одна от другой. Тогда относительное время совместной работы всех комбайнов равно… 1) 1,7 2) 0,765 3) 0,68 +4) 0,612 5) другой вариант ответа 1. Два стрелка производят по одному выстрелу. Вероятность попадания в цель для первого-0,5, и для второго стрелка равна 0,3. Тогда вероятность того, что оба стрелка попадут в цель, равна… 1) 0,18 +2) 0,15 3) 0,28 4) 0,8 5) другой вариант ответа 2. В посевах пшеницы 95% здоровых растений. Выбирают два растения. Тогда вероятность того, что оба растения не дадут всходы, равна… 1) 0,95 2) 1,9 3) 0,05 +4) 0,0025 5) другой вариант ответа 3. Три стрелка произвели залп по цели. Вероятность поражения цели первым стрелком равна 0,7; вторым-0,8; третьим-0,9. Тогда вероятность того, что все три стрелка промахнутся, равна... +1) 0,006 2) 0,06 3) ,0002 4) 0,003 5) другой вариант ответа 4. В посевах пшеницы 90% здоровых растений. Выбирают три растения. Вероятность того, что все три растения дадут всходы… +1) 0,729 2) 0,9 3) 0,81 4) 0,99 5) другой вариант ответа 5. В корзине 18 саженцев двух сортов, из них 8 сорта А, остальные сорта В. Выбирают два саженца. Вероятность того, что оба саженца сорта В, равна… 1) 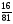 +2) 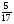 3) 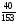 4) 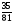 5) другой вариант ответа 6. В коробке 7 карандашей синих и 9 карандашей красных. Выбирают три карандаша. Вероятность того, что они все синие равна… +1) 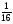 2) 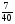 3) 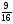 4) 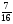 5) другой вариант ответа 7. В лазерной группе 15 конструкторов, из них 4 женщины. Для работы над секретным объектом выбирают двоих. Тогда вероятность того, что это женщины равна… 1) 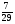 2) 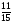 +3) 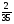 4) 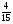 5) другой вариант ответа 8. В ящике 13 радиоламп двух видов, из них 7 ламп вида В, остальные вида А. Выбирают три лампы. Тогда вероятность того, что все три лампы вида А равна … 1) 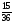 +2) 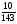 3) 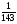 4) 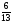 5) другой вариант ответа 9. Эффективность вакцины в формировании иммунитета составляет 75%. Вакцинировали двух животных. Вероятность того, что оба животных приобрели иммунитет, равна… 1) 0,75 2) 0,4375 3) 0,0625 +4) 0,5625 5) другой вариант ответа 10. Семена первого сорта имеют всхожесть 92%, второго сорта-85%. Отбирается по одному зерну каждого сорта. Вероятность того, что оба зерна дадут всходы, равна… +1) 0,782 2) 0,218 3) 0,177 4) 1 5) другой вариант ответа 1. Вероятность выпадения числа очков, кратного четырем, при одном подбрасывании кубика +1) 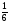 ; ;2) 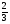 ; ;3) 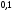 ; ;4) 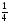 . .2. Игральная кость бросается один раз. Вероятность того, что появится менее двух очков, равна … +1) 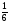 ; ;2) 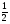 ; ;3) 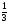 ; ;4) 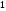 . .3. По расчетам вероятность появления некоторого события равна числу 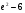 . Тогда можно сделать вывод о том, что … . Тогда можно сделать вывод о том, что …1) событие достоверно; 2) событие невозможно; +3) расчеты неверны; 4) событие случайно. 4. Вероятность того, что первого января наудачу выбранного года будет пятница, равна … 1) 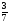 ; ;+2) 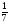 ; ;3) 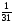 ; ;4) 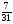 . .5. Брошены две игральные кости. Тогда вероятность того, что сумма выпавших очков будет меньше четырех, равна … +1) 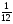 ; ;2) 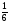 ; ;3) 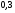 ; ;4) 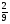 . .6. Вероятность выпадения числа очков, кратного пяти, при одном подбрасывании кубика равна … 1) 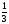 ; ;+2) 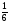 ; ;3) 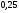 ; ;4) 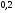 . .7. На полке 24 книги по теории вероятностей, 8 из них в мягком переплете, остальные – в твердом. Тогда вероятность того, что наудачу взятая с полки книга в твердом переплете равна … 1) 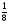 ; ;2) 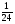 ; ;3) 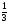 ; ;+4) 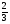 . .8. По расчетам вероятность появления некоторого события равна числу 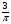 . Тогда можно сделать вывод о том, что … . Тогда можно сделать вывод о том, что …1) событие достоверно; 2) событие невозможно; 3) расчеты неверны; +4) событие случайно. 9. Игральная кость бросается один раз. Вероятность того, что появится более четырех очков, равна: 1) 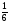 ; ;2) 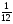 ; ;3) 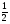 ; ;+4) 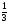 . .10. В урне находится 15 шаров, пять из которых красные, а остальные белые. Наудачу вынимают один шар. Какова вероятность того, что он белый? 1) 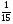 ; ;+2) 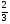 ; ;3) 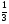 ; ;4) 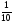 . .11. В группе студентов 18 юношей и 7 девушек. Тогда вероятность того, что первый по списку студент – юноша, равна … 1) 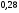 ; ;2) 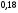 ; ;+3) 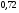 ; ;4) 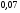 . .12. Вероятность того, что при случайном расположении в ряд четырех букв разрезной азбуки, на которых написаны Е, С, Н, Г, получится слово «СНЕГ», равна… 1) 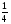 ; ;2) 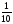 ; ;+3) 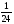 ; ;4) 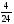 . .13. В ящике 20 деталей, из которых 8 – стандартных. Найти вероятность того, что взятые наудачу две детали окажутся стандартными: 1) 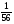 ; ;2) 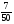 ; ;3) 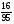 ; ;+4) 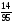 . .14. В бригаде 10 человек, из них 4 женщины. Наудачу, по табельным номерам, на дежурство выбираются двое. Тогда вероятность того, что будут выбраны только мужчины, равна … +1) 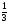 ; ;2) 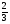 ; ;3) 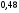 ; ;4) 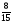 . .15. Куб, все грани которого окрашены, распилен на 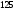 кубиков одинакового размера. Тогда вероятность того, что наудачу извлеченный кубик имеет три окрашенных грани, равна … кубиков одинакового размера. Тогда вероятность того, что наудачу извлеченный кубик имеет три окрашенных грани, равна …1) 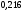 ; ;+2) 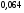 ; ;3) 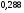 ; ;4) 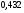 . .16. Слово «молния» разрезали на буквы и выложили наудачу три из них в ряд. Тогда вероятность получить слово «лом» равна … 1) 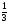 ; ;2) 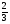 ; ;3) 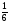 ; ;+4) 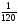 . .[Повторные независимые испытания, 1] 1. В данном хозяйстве за последние годы в среднем от 100 коров получали ежегодно 52 телочки. Тогда наиболее вероятное число ожидаемого получения телочек в этом году от 225 тельных коров в хозяйстве равно … 1) 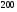 ; ;+2) 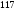 ; ;3) 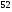 ; ;4) 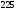 . .2. На инкубационную закладку поступила партия из 1000 яиц. Вероятность того, что в результате инкубации каждого яйца появится цыпленок, равна 0,75. Тогда наиболее вероятное число вылупившихся цыплят равно … 1) 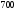 ; ;+2) 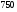 ; ;3) 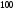 ; ;4) 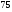 . .3. Число коротких волокон в партии хлопка составляет 25% всего количества волокон. Если наивероятнейшее число коротких волокон в нем 150, то в отдельно взятом пучке волокон должно быть… 1) 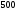 ; ;+2) 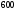 ; ;3) 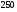 ; ;4) 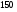 . .4. Эффективность вакцины составляет 90%. Наудачу выбираются 10 животных. Тогда наиболее вероятное число животных среди отобранных, которые приобрели иммунитет… 1) 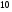 ; ;+2) 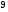 ; ;3) 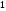 ; ;4) 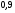 . .5. Вероятность того, что при шести подбрасываниях монеты, «орел» выпадет ровно 1 раз, равна … 1) 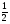 ; ; 2) 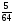 ; ;3) 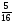 ; ;+4) 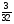 . .6. Вероятность выживания бактерии после радиоактивного облучения равна 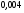 . Тогда вероятность того, что после облучения из 200 бактерий останется менее двух, равна … . Тогда вероятность того, что после облучения из 200 бактерий останется менее двух, равна …1) 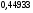 ; ;2) 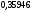 ; ;+3) 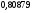 ; ;4) 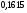 . .7. Найти вероятность того, что при шести подбрасываниях монеты, «орел» выпадет ровно 2 раза. 1) 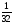 ; ;2) 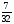 ; ;+3) 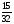 ; ;4) 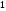 . .8. Проверяется книга в 1000 страниц на наличие опечаток. Вероятность опечатки на каждой странице равна 0,004. Вероятность того, что в книге нет опечаток, равна … +1) 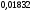 ; ;2) 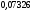 ; ;3) 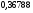 ; ;4) 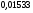 . .[ДСВ и законы распределений, 1] 1. Дан закон распределения дискретной случайной величины 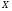 : :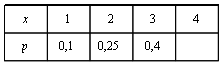 . Тогда вероятность того, что случайная величина . Тогда вероятность того, что случайная величина 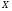 примет значение 4 равна … примет значение 4 равна …1) 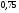 +2) 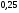 3) 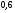 4) 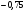 . .2. Задан закон распределения ДСВ:  . Тогда вероятность . Тогда вероятность 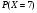 равна … равна …1) 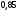 2) 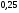 3) 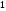 +4) 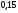 3. Задан закон распределения ДСВ:  . Тогда вероятность . Тогда вероятность 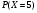 равна … равна …1) 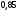 2) 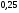 3) 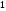 +4) 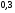 4. Дан закон распределения дискретной случайной величины 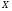 : :  . Тогда значение . Тогда значение  равно … равно …1) 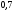 +2) 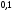 3) 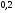 4) 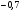 . .5. Дан закон распределения дискретной случайной величины 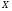 : :  . Тогда значение . Тогда значение  равно … равно …1) 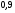 +2) 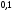 3) 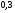 4) 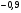 . .6. Задан закон распределения ДСВ:  . Тогда вероятность . Тогда вероятность 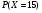 равна … равна …Ответ: 0,5 7. ДСВ задана законом распределения вероятностей:  . Тогда ее математическое ожидание равно . Тогда ее математическое ожидание равно 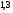 , если … , если …1) 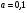 , , 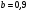 2) 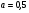 , , 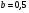 3) 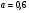 , , 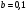 +4) 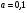 , , 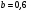 [Числовые характеристики ДСВ, 1] 1. Пусть 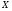 – дискретная случайная величина, заданная законом распределения вероятностей: – дискретная случайная величина, заданная законом распределения вероятностей: 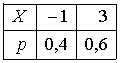 . Тогда дисперсия этой случайной величины равна… . Тогда дисперсия этой случайной величины равна…1) 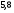 ; ;2) 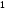 ; ;3) 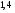 ; ;+4) 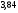 . .2. Случайная величина 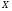 принимает одно и тоже значение, равное принимает одно и тоже значение, равное 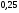 . Тогда математическое ожидание случайной величины равно … . Тогда математическое ожидание случайной величины равно …1) 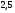 ; ;2) 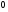 ; ;3) 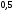 ; ;+4) 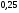 . .3. Задан закон распределения ДСВ:  . Тогда математическое ожидание равно … . Тогда математическое ожидание равно … Ответ: 26 4. Известно, что 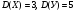 . Тогда . Тогда 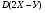 равно … равно …Ответ: 17 5. Задан закон распределения ДСВ:  . Тогда математическое ожидание этой ДСВ равно … . Тогда математическое ожидание этой ДСВ равно …1) 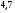 +2) 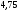 3) 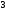 4) 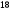 7. Задан закон распределения ДСВ:  . Тогда математическое ожидание этой ДСВ равно … . Тогда математическое ожидание этой ДСВ равно …1) 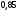 +2) 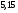 3) 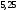 4) 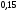 8. Случайная величина 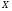 принимает одно и тоже значение, равное принимает одно и тоже значение, равное 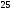 . Тогда среднее квадратическое отклонение случайной величины равно … . Тогда среднее квадратическое отклонение случайной величины равно …Ответ :0 9. Пусть 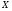 – дискретная случайная величина, заданная законом распределения вероятностей: – дискретная случайная величина, заданная законом распределения вероятностей:  . Тогда математическое ожидание этой случайной величины равно… . Тогда математическое ожидание этой случайной величины равно…Ответ: 1,4 10. Случайная величина 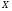 принимает одно и тоже значение, равное принимает одно и тоже значение, равное 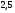 . Тогда дисперсия случайной величины равна … . Тогда дисперсия случайной величины равна …Ответ: 0 [Нормальный закон распределения, 1] 1. Известно, что 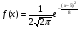 . Тогда кривая нормального распределения выпукла на промежутке … . Тогда кривая нормального распределения выпукла на промежутке …1) 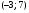 ; ;+2) 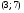 ; ;3) 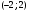 ; ;4) 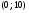 . .2. Известно, что 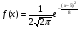 . Тогда кривая нормального распределения симметрична относительно прямой … . Тогда кривая нормального распределения симметрична относительно прямой …1) 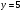 ; ;2) 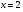 ; ;+3) 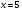 ; ;4) 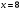 . .3. Известно, что 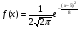 . Тогда дисперсия равна… . Тогда дисперсия равна…Ответ: 4 4. Известно, что 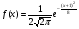 . Тогда математическое ожидание . Тогда математическое ожидание 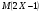 равно… равно… 1) 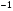 2) 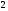 3) 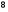 +4 |
