Основные понятия математической логики

• Название: Основные понятия математической логики
• Дата: 05.12.2022
• Размер: 2.35 Mb.
• Имя файла: ege15 (2).doc
• Тип: Закон; #828321
• страница: 11 из 50

Ещё пример задания:

Р-20 (М.В. Кузнецова). Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа А формула

ДЕЛ(x, А)  (ДЕЛ(x, 21) + ДЕЛ(x, 35))

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

Решение:

1. 
   введём обозначения A = ДЕЛ(x, А), D₂₁ = ДЕЛ(x, 21) , D₃₅ = ДЕЛ(x, 35)
   
2. 
   введём множества:
   

A –множество натуральных чисел, для которых выполняется условие A

D₂₁ –множество натуральных чисел, для которых выполняется условие D₂₁

D₃₅ –множество натуральных чисел, для которых выполняется условие D₃₅

…

3. 
   Запишем формулу из условия в наших обозначениях
   

4. 
   Раскроем импликацию по правилу :
   

5. 
   Чтобы формула была тождественно истинной необходимо, чтобы (т.е. ), когда . Тогданаибольшее множество А определяется как
   
6. 
   Множество , точно соответствующее выражению с помощью функции ДЕЛ получить невозможно.
   
7. 
   Выполним анализ исходной формулы с помощью кругов Эйлера.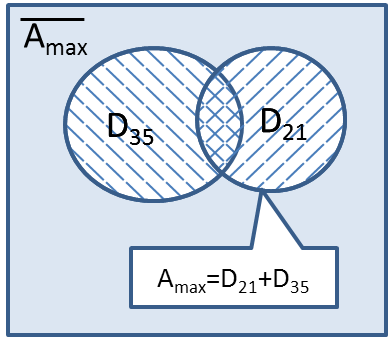
   

Чтобы в множество входили все числа, не попавшие в объединение , достаточно, чтобы множество А находилось внутри этого объединения, например, совпадая с одним из множеств D₃₅ или D₂₁, или располагаясь внутри любого из них, что возможно, если использовать делители, кратные 21 или 35.

8. 
   В задании требуется найти НАИМЕНЬШЕЕ значение, этому условию соответствует 21.
   
9. 
   Ответ: 21
   

Ещё пример задания:

Р-19 (М.В. Кузнецова). Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа А формула

¬ДЕЛ(x, А)  (¬ДЕЛ(x, 21) ¬ ДЕЛ(x, 35))

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

Решение:

1. 
   введём обозначения A = ДЕЛ(x, А), D₂₁ = ДЕЛ(x, 21) , D₃₅ = ДЕЛ(x, 35) и D_N = ДЕЛ(x, N)
   
2. 
   введём множества:
   

A –множество натуральных чисел, для которых выполняется условие A

D₂₁ –множество натуральных чисел, для которых выполняется условие D₂₁

D₃₅ –множество натуральных чисел, для которых выполняется условие D₃₅

…

3. 
   Запишем формулу из условия в наших обозначениях
   

4. 
   Раскроем импликацию по правилу :
   

5. 
   Чтобы формула была тождественно истинной необходимо, чтобы А = 1, когда . Тогдамножество А определяется так:
   
6. 
   Множество , точно соответствующее выражению с помощью функции ДЕЛ получить невозможно.
   
7. 
   Выполним анализ исходной формулы с помощью кругов Эйлера.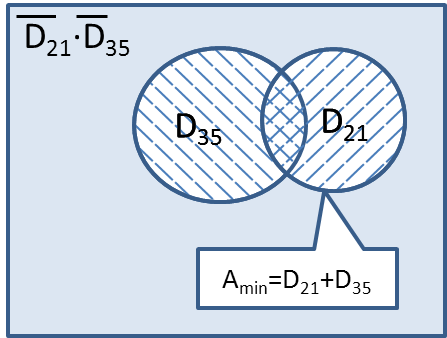
   

в множество А должны входить все числа, попавшие в объединение . Нужно найти множество, в которое входят оба эти множества. Для этого рассмотрим делители чисел 21 и 35.

8. 
   Число 35 делится на 5 и 7, поэтому: , 21 делится на 3 и 7, поэтому:
   
9. 
   Перепишем и упростим формулу для А:
   
10. 
    Таким образом, каждое из множеств D₃₅ и D₂₁ входит в множество D₇ . Объединение D₃₅ + D₂₁ тоже входит в D₇. Поскольку 7 – наибольший общий делитель чисел 21 и 35, то найдено максимальное значение соответствующее условию задачи.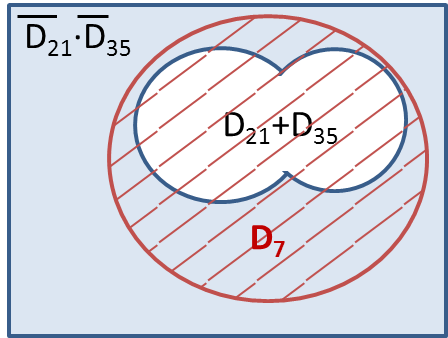
    

11. 
    Ответ: 7.