Основные понятия математической логики

Название	Основные понятия математической логики
Дата	05.12.2022
Размер	2.35 Mb.
Формат файла
Имя файла	ege15 (2).doc
Тип	Закон #828321
страница	2 из 50

1 2 3 4 5 6 7 8 9 ... 50

Задачи с поразрядными операциями

Как вычислять выражение с поразрядными операциями

В задачах ЕГЭ до настоящего времени использовалась только поразрядная логическая операция «И» (она обозначается символом &), которая выполняется между соответствующими битами двоичной записи двух целых чисел. Не забывайте, что

Результат поразрядной операции между целыми числами – это целое число!.

Например, найдём результат поразрядной операции 29 & 11:

29 = 11101₂

11 = 01011₂

9 = 01001₂

Серым фоном отмечены биты, которые в обоих числах равны 1. Только они и будут равны 1 в числе-результате. Таким образом, 29 & 11 = 9.

Теперь найдём результат операции (29 & 11 = 0). Не забывайте, что

Результаты операций (a & b = 0) и (a & b  0) – это логические значения (истина/ложь)!.

Вычислим значение выражения:

( (x & 26 = 0)  (x & 13 = 0))  ((x & 78  0)  (x & A = 0))

при x = 5, A = 57:

( (5 & 26 = 0)  (5 & 13 = 0))  ((5 & 78  0)  (5 & 57 = 0))

Вычисляем результаты поразрядного И (это числа!):

5 & 26 = 0 5 & 13 = 5
5 & 78 = 4 5 & 57 = 1

Теперь вычисляем логические значения (И – истина, Л – ложь):

(5 & 26 = 0) = И (5 & 13 = 0) = Л
(5 & 78  0) = И (5 & 57 = 0) = Л

Наконец, подставляем эти логические значения в заданное выражение:

(И  Л)  (И  Л)
И  Л = Л

При заданных условиях выражение ложно.

Решение задач с поразрядными операциями

Для решения этих задач удобно применять метод, предложенный А.В. Здвижковой (г. Армавир) и обоснованный автором^². Введём обозначения

Это означает, что если истинно

, то это равносильно тому, что истинно

. Для сокращения записи вместо

будем писать просто

.

Пусть в двоичной записи числа K бит с номером i, обозначаемый как k_i, равен 1. Если при этом для некоторого x выполнено условие

, то соответствующий i-й бит в двоичной записи числа x равен нулю, так как должно выполняться условие

.

Для преобразования выражений полезно следующее свойство:

где «or» означает поразрядную дизъюнкцию между двумя натуральными числами. Для доказательства предположим, что в двоичной записи числа K биты с номерами i₁, i₂, …, i_q равны 1, а остальные равны 0; а в двоичной записи числа M биты с номерами j₁,j₂, …, j_p равны 1, а остальные равны 0. Истинность выражения в левой части означает, что все биты числа x, входящие во множества B_K = {i₁, i₂, …, i_q} и B_M = {j₁,j₂, …, j_p} одновременно равны нулю. Поэтому любая комбинация битов из этих множеств тоже равна нулю. Это справедливо, в том числе, и для множества, которое представляет собой объединение множеств B_Kи B_M, то есть, для множества единичных битов числа KorM.

Самый важный результат можно сформулировать так:

Условие

истинно для любых натуральных значений x тогда и только тогда, когда все единичные биты двоичной записи числа M входят во множество единичных битов двоичной записи числа K.

Доказательство. Пусть в двоичной записи числа K биты с номерами i₁, i₂, …, i_q равны 1, а остальные равны 0. Пусть также

истинно для некоторого x, это значит, что в числе x биты с теми же номерами – нулевые. Если все единичные биты двоичной записи числа M входят во множество B_K = {i₁, i₂, …, i_q}, то истинно и высказывание

, а следовательно – высказывание

(1  1 = 1). Если же хотя бы один бит двоичной записи числа M не входит во множество B_K (пусть это будет бит с номером j), то для тех х, у которых все биты из множества B_K нулевые, а бит j равен 1, выполняется

, но не выполняется

, так что высказывание

ложно.

Для упрощения выражений полезен следующий результат:

Условие

при любых натуральных K, M и N ложно для некоторых натуральных значений x.

Идея доказательства состоит в том, чтобы представить импликацию в виде произведения двух импликаций:

.

Вторая импликация в правой части ложна хотя бы для некоторых x, поскольку из того, что некоторые биты числа x равны нулю (выполняется

) совершенно не следует, что какие-то другие (или те же самые) биты того же числа ненулевые (выполняется

). Строгое доказательство дано в статье, ссылка на которую приведена в сноске на предыдущей странице.

Метод, предложенный А.В. Здвижковой заключается в следующем:

упростить заданное выражение, сведя его к импликации, в которой нет инверсий
применить полученные выше результаты для нахождения всех подходящих значений неизвестного числа a, включая минимальное и максимальное значения.

Этот же метод можно применить и в том случае, когда результат поразрядной операции «И» сравнивается не с нулём, а с другими числами. Например, рассмотрим выражение R = (x&125 5). Переведём числа в двоичную систему:

6 5 4 3 2 1 0

125 = 1111101₂

5 = 101₂.

Истинность R означает, что

биты числа x с номерами 3, 4, 5 и 6 равны 0;
биты числа x с номерами 0 и 2 равны 1.

С учётом введённых выше обозначений можно записать эквивалентное условие:

R = (x&125 5) 

.

Применяя операцию «НЕ» к этому выражению, получаем

= (x&125 5) 



.

В общем виде для чисел b и c, таких, что множество единичных битов числа c входит во множество единичных битов числа b, имеем

R = (x& b c) 

= (x& b c) 

.

где c₁,c₂, …, c_q – степени числа 2, которые соответствуют единичным битам числа c. Например, для
c = 5 = 101₂ имеем c₁ = 2² = 4,c₂ = 2⁰ = 1.

Пример задания:

Р-35 (демо-2021). Обозначим через ДЕЛ(n,m) утверждение «натуральное число n делится без

остатка на натуральное число m». Для какого наибольшего натурального числа А формула

¬ДЕЛ(x,А)(ДЕЛ(x,6) ¬ДЕЛ(x,9))

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

Решение (теоретическое):

для сокращения записи введём обозначения:

ДЕЛ(x,А) = A

ДЕЛ(x,6) = D₆

ДЕЛ(x,9) = D₉

перепишем выражение в виде
используя формулу , раскроем первую импликацию:

и вторую:

согласно правилу де Моргана , так что

сведём выражение к единственной импликации

сформулируем правило, которое мы получили: если значение x делится на 6 и делится на 9, то оно делится на A;
если значение x делится на 6 и делится на 9, то оно делится на наименьшее общее кратное НОК(6,9)=18, поэтому наибольшее значение A, удовлетворяющее условию, равно 18
Ответ: 18.

Решение (с помощью программы):

для проверки решения (при наличии времени) можно использовать программу; напишем её на языке Python
определим логическую функцию Del с двумя аргументами, которая проверяет делимость первого аргумента x на второй аргумент D (если x делится на D, возвращается True)

def Del( x, D ):

return x % D == 0

Функция названа Del с большой буквы, чтобы её имя отличалось от команды удаления del.

теперь определим функцию f(x,A), которая вычисляет заданное нам выражение:

def f( x, A ):

return (not Del(x,A)) <= (Del(x,6) <= (not Del(x,9)))

здесь импликация заменяется на <= (спасибо за идею А. Сидорову) с учётом того, что

False < True; проверим правильность такой замены по таблице истинности операции импликация:

A	B	AB	A<=B
0	0	1	1
0	1	1	1
1	0	0	0
1	1	1	1

основная программа проверяет выражение на истинность полным перебором (методом «грубой силы», англ. bruteforce) для возрастающих значений A; предполагаем, что наибольшее A меньше, чем 1000; тогда

for A in range(1, 1000):

if A подходящее:

print( A )

что значит «А подходящее»? Это означает, что при всех натуральных x выражение f(x) истинно; это можно проверить перебором, скажем, для всех x, меньших 1000:

for A in range(1,1000):

OK = True

for x in range(1,1000):

if not f(x,A):

OK = False

break

if OK:

print( A )

блок, выделенный серым фоном – это проверка очередного значения А; сначала логическая переменная OK равна True (все хорошо); если для какого-то x функция f(x) вернула значение False (ложь), переменной OK присваивается значение False (это А не подходит) и цикл заканчивается досрочно с помощью оператора break (остальные значения x проверять нет смысла, всё уже понятно)
если внутренний цикл отработал и переменная OK осталась равной True, то А подходит и выводится на экран
программа выводит

1

2

3

6

9

18

ответом будет последнее выведенное значение А, равное 18

Ответ: 18.

В некоторых случаях диапазона [1;999], который используется при переборе значений A и x, может не хватить для правильного решения задачи. Например, при некотором A программа просто не дойдёт до значения x > 999, при котором нарушится истинность высказывания, и это А будет принято за правильный ответ. Поэтому лучше увеличивать диапазон перебора до 10000-50000, по крайней мере, для переменной x.

приведём полную программу:

def Del( x, D ):

return x % D == 0
def f( x, A ):

return (not Del(x,A)) <= (Del(x,6) <= (not Del(x,9)))
for A in range(1,1000):

OK = True

for x in range(1,1000):

if not f(x,A):

OK = False

break

if OK:

print( A )

Для других задач этого типа достаточно заменить логическое выражение в функции f(x).

возможна краткая, но менее понятная форма программы без функций, использующая вперемежку числовые и логические значения и операции с ними (А. Сидоров, https://www.youtube.com/watch?v=vdIIelsomkM):

for A in range(1,1000):

OK = 1

for x in range(1,1000):

OK *= (x % A != 0) <= ((x % 6 == 0) <= (x % 9 != 0))

if OK:

print( A )

При умножении ложное значение равносильно нулю, поэтому если хотя бы для одного значения x условие не выполняется, переменная OK в конце внутреннего цикла будет равна 0.

Решение (с помощью программы, И. Моисеев):

напишем понятную форму программы без функций; преобразования, используя формулу , получаем выражение:

ДЕЛ(x,А) V ¬ (ДЕЛ(x,6) V ¬ДЕЛ(x,9)

Так как формула должна быть тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х), то необходимо, чтобы выполнилось хоть одно условие в этом выражении.

программа проверяет выражение на истинность каждое слагаемое полным перебором для возрастающих значений A; предполагаем, что наибольшее A не превышает 1000, тогда

a = [] # массив хранения значений А

for A in range(1,1001):

countX = 0

for x in range(1,1001):

if (x%A == 0) or not(x%6 == 0) or not(x%9 == 0):

countX += 1

if countX == 1000:#все числа Х перебрали

a.append(A)

print( max(a) )

если после отработки внутреннего цикла переменная countX стала равна 1000, то это говорит о том, что при всех числах Х хоть одно из слагаемых будет равно True; тогда текущее значение А подходит и записывается в массив a
после работы программы в массиве оказываются значения:

1

2

3

6

9

18

функция max(a) позволяет определить ответ – наибольшее значение А, равное 18

Ответ: 18.

Ещё пример задания:

Р-34. (С.С. Поляков) Укажите наименьшее целое значение А, при котором выражение

(5k + 6n > 57) ∨ ((k ≤ A)  (n < A))

истинно для любых целых положительных значений k и n.

Решение:

особенность этой задачи – «уход» авторов от привычных обозначений переменных, x и y; поскольку мы будем работать с графиками на плоскости, удобнее всё же вернуться к стандартным переменным x и y(понятно, что результат от этого не изменится)

(5x + 6y > 57) ∨ ((x ≤ A)  (y < A))

первое выражение (5x + 6y > 57) не зависит от выбора A
таким образом, нам нужно выбрать значение A так, чтобы условие

(x < A) and (y ≤ A)

выполнялось при всех x и y, для которых ложно (5x + 6y > 57), то есть истинно

(5x + 6y  57)

Нужно также учесть, что x и y положительны и добавить ещё два ограничения:

(x  1 )and (y  1), таким образом, получаем треугольник, ограниченный линиями

(5x + 6y = 57) and (x  1 ) and (y  1)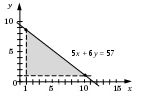

для всех точек этого треугольника с целочисленными координатами должно выполняться условие

(x ≤ A)  (y < A)

это значит, что треугольник (точнее, все его точки с целочисленными координатами) должен оказаться внутри квадрата со стороной A, причем в силу нестрогого неравенства (x ≤ A) правая граница квадрата (она выделена жирной синей линией) может совпадать с точками треугольника:

находим точку пересечения прямых 5x + 6y = 57 и x= 1: y  8,67; поскольку нужно выполнить условие (y < A) , получаем A > 8
находим точку пересечения прямых 5x + 6y = 57 и y= 1: x = 10,2; поскольку нужно выполнить условие (x  A) , получаем A  10
оба условия нужно выполнить одновременно, поэтому выбираем наиболее жёсткое: A 10, что даёт A_min= 10.
Ответ: 10.
заметим, что эту простую задачу можно было решать и аналитически, учитывая, что нам достаточно рассматривать не все точки треугольника, а только отрезок прямой 5x + 6y = 57, ограниченный прямыми x= 1 и y= 1: если все точки этого отрезка окажутся внутри красного квадрата, то и все остальные точки треугольника тоже будут внутри красного квадрата; поэтому находим максимальную целочисленную координату y на отрезке:

5x + 6y = 57 и x= 1: y  8,67  y_max = 8

затем – максимальную целочисленную координату x на отрезке:

5x + 6y = 57 и y= 1: x = 10,2  x_max = 10

и выбираем наименьшее A, при котором (y_max < A) и (x_max  A), то есть A_min = 10

Решение (программа на Python, Г.М. Федченко):

программа на Python, полный перебор:

def f( k, n, A ):

return (5*k + 6*n > 57) or (k <= A) and (n < A)
for A in range(1,1000):

OK = True

for k in range(1,1000):

for n in range(1,1000):

if not f(k, n, A):

OK = False

break

if OK:

print( A )

break

вариант без функции:

for A in range(1,1000):

OK = 1

for k in range(1,1000):

for n in range(1,1000):

OK *= (5*k + 6*n > 57) or (k <= A) and (n < A)

if not OK: break

if OK:

print( A )

break

Ответ: 10.

Ещё пример задания:

Р-33. (С.С. Поляков) Укажите наибольшее целое значение А, при котором выражение

(y – x  5) ∨ (A < 2x³ + y) ∨ (A < y² + 16)

истинно для любых целых положительных значений x и y.

Решение:

первое выражение (y – x  5) не зависит от выбора A
таким образом, нам нужно выбрать значение A так, чтобы условие

(A < 2x³ + y) or (A < y² + 16)

выполнялось при всех x и y, для которых ложно (y – x  5), то есть истинно

(y – x = 5) или y = x + 5

нарисуем линию y = x + 5. Нужно также учесть, что x и y положительны

и добавить ещё два ограничения: (x  1 )and (y  1).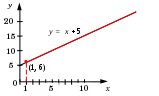

находим точку пересечения прямых y = x + 5 и x= 1: (x = 1, y = 6);
по условию задачи нужно, чтобы для всех точек прямой y = x + 5 справа от точки (1, 6) (они выделены красным цветом) было выполнено условие (A < 2x³ + y) or (A < y² + 16)
поскольку два условия связаны с помощью операции ИЛИ, достаточно выполнения одного из этих условий
рассмотрим условие (A < 2x³ + y); минимальные значения x и y из всех точек красного луча имеет крайняя точка (1, 6), причём здесь достигается одновременно и минимум x, и минимум y; поэтому получаем (A < 2x³ + y)  (A < 2·1³ + 6)  (A < 8)
для второго условия (A < y² + 16) также рассматриваем самое жёсткое ограничение – в точке (1, 6), где значение y минимально; получаем (A < 6² + 16)  (A < 52)
Поскольку должно выполняться одно из условий (A < 8) or (A < 52), выбираем наименее жёсткое: (A < 52)
Ответ: 51.

Решение (программа на Python, Г.М. Федченко):

программа на Python, полный перебор:

def f( x, y, A ):

return (y - x != 5) or (A < 2*x**3 + y) or (A < y**2 + 16)
for A in range(1,100):

OK = True

for k in range(1,1000):

for n in range(1,1000):

if not f(k, n, A):

OK = False

break

if OK:

print( A )

ещё один вариант с функцией (перебор значений A в порядке убывания):

def f( x, y, A ):

return (y - x != 5) or (A < 2*x**3 + y) or (A < y**2 + 16)
for A in range(100, 0, -1):

OK = True

for k in range(1,1000):

for n in range(1,1000):

if not f(k, n, A):

OK = False

break

if OK:

print( A )

break

вариант без функции:

for A in range(1,100):

OK = 1

for x in range(1,1000):

for y in range(1,1000):

OK *= (y - x != 5) or (A < 2*x**3 + y) or (A < y**2 + 16)

if not OK: break

if OK:

print( A )

ещё один вариант без функции:

for A in range(100, 0, -1):

OK = 1

for x in range(1,1000):

for y in range(1,1000):

OK *= (y - x != 5) or (A < 2*x**3 + y) or (A < y**2 + 16)

if not OK: break

if OK:

print( A )

break

Ответ: 51.

1 2 3 4 5 6 7 8 9 ... 50