Основные понятия математической логики

• Название: Основные понятия математической логики
• Дата: 05.12.2022
• Размер: 2.35 Mb.
• Имя файла: ege15 (2).doc
• Тип: Закон; #828321
• страница: 3 из 50

Ещё пример задания:

Р-32. Укажите наибольшее целое значение А, при котором выражение

(y + 2x  99) ∨ (y > A) ∨ (x > A)

истинно для любых целых положительных значений x и y.

Решение:

1. 
   первое выражение не зависит от выбора A: (y +2x  99)
   
2. 
   таким образом, нам нужно выбрать значение A так, чтобы условие (y > A) or (x > A)
   

выполнялось при всех x и y, для которых ложно (y +2x  99), то есть истинно (y +2x = 99) или y = –2x + 99

3. 
   нарисуем линию y = –2x + 99, а также заштрихуем область (y > A) or (x > A) для некоторого значения A, например, для A = 50 (конечно, нужно учесть, что x и y положительны и добавить ещё два ограничения: (x > 0)and (y > 0)):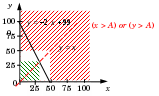
   

4. 
   по условию задачи нужно, чтобы все точки отрезка прямой y = –2x + 99 в первой четверти плоскости оказались в заштрихованной зоне
   
5. 
   поэтому все точки образовавшегося белого квадрата, в том числе и его вершина (A, A), должны находиться строго под этим отрезком; такой квадрат, соответствующий максимальному значению A, выделен на рисунке зелёной штриховкой
   
6. 
   находим координаты вершины зелёного квадрата: находим точку пересечения прямых y = –2x + 99 и y = x; эта задача сводится к линейному уравнению x = –2x + 99 решение которого – x = 33
   
7. 
   значение A должно быть меньше этого x, поэтому максимальное значение A= 32
   
8. 
   Ответ: 32.
   

Ещё пример задания:

Р-31. Укажите наименьшее целое значение А, при котором выражение

(y + 3x < A) ∨ (2y +x > 50) ∨ (4y – x < 40)

истинно для любых целых положительных значений x и y.

Решение:

1. 
   второе и третье выражения не зависят от выбора A: (2y +x > 50) or (4y – x < 40)
   
2. 
   таким образом, нам нужно выбрать значение A так, чтобы условие (y + 3x < A)
   

выполнялось при всех x и y, для которых ложно (2y +x > 50) or (4y – x < 40), то есть истинно

(2y +x  50) and (4y – x  40)

3. 
   последние два условия можно переписать в виде
   

(y  – x/2 + 25) and (y  x/4 + 10)

4. 
   поскольку по условию x и y должны быть положительны, добавляем ещё два условия:
   

(y  – x/2 + 25) and (y  x/4 + 10) and (x > 0) and (y > 0)

5. 
   изобразим схематично на плоскости x – y эту область (она заштрихована):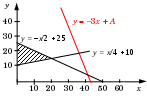
   

6. 
   для всех точек этой области должно выполняться условие y + 3x < A, равносильное условию
   

y < – 3x +A

7. 
   это значит, что вся область должна лежать ниже линии y = – 3x +A; одна такая подходящая линия показана на рисунке сверху
   
8. 
   из рисунка видно, что при параллельном переносе вниз, соответствующем изменению A, она коснётся заштрихованной области в правой вершине заштрихованного треугольника
   
9. 
   найдём эту точку пересечения:
   

y = – x/2 + 25 = x/4 + 10  x = 20, y = 15

10. 
    поэтому допустимые значение A определяются условием:
    

15 < – 320 +A  A > 75

откуда следует, что A_min = 76.

11. 
    Ответ: 76.
    

Примечание: фактически эта задача представляет собой задачу целочисленного линейного программирования, на что впервые обратил внимание Б.А. Державец³.

Решение (программа на Python, Г.М. Федченко):

1. 
   программа на Python, полный перебор:
   

def f( x, y, A ):

return (y + 3*x < A) or (2*y + x > 50) or (4*y - x < 40)
for A in range(1, 200):

OK = True

for x in range(1,1000):

for y in range(1,1000):

if not f(x, y, A):

OK = False

break

if OK:

print( A )

break

2. 
   вариант без функции:
   

for A in range(1, 200):

OK = 1

for x in range(1,1000):

for y in range(1,1000):

OK *= (y + 3*x < A) or (2*y + x > 50) or (4*y - x < 40)

if not OK: break

if OK:

print( A )

break

3. 
   Ответ: 76.