Основные понятия математической логики

• Название: Основные понятия математической логики
• Дата: 05.12.2022
• Размер: 2.35 Mb.
• Имя файла: ege15 (2).doc
• Тип: Закон; #828321
• страница: 4 из 50

Ещё пример задания:

Р-30. Укажите наименьшее целое значение А, при котором выражение

(y + 2x < A) ∨ (3y +2x > 120) ∨ (3y – x > 30)

истинно для любых целых положительных значений x и y.

Решение:

1. 
   второе и третье выражения не зависят от выбора A: (3y +2x > 120) or (3y – x > 30)
   
2. 
   таким образом, нам нужно выбрать значение A так, чтобы условие (y + 2x < A)
   

выполнялось при всех x и y, для которых ложно (3y +2x > 120) or (3y – x > 30), то есть истинно

(3y +2x  120) and (3y – x  30)

3. 
   последние два условия можно переписать в виде
   

(y  – 2x/3 + 40) and (y  x/3 + 10)

4. 
   поскольку по условию x и y должны быть положительны, добавляем ещё два условия:
   

(y  – 2x/3 + 40) and (y  x/3 + 10) and (x > 0) and (y > 0)

5. 
   изобразим схематично на плоскости x – y эту область (она заштрихована):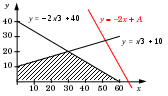
   

6. 
   для всех точек этой области должно выполняться условие y + 2x < A, равносильное условию
   

y < – 2x +A

7. 
   это значит, что вся область должна лежать ниже линии y = – 2x +A; одна такая подходящая линия показана на рисунке сверху
   
8. 
   поскольку коэффициент наклона этой линии (–2) по модулю больше, чем коэффициент прямой y = – 2x/3 + 40, при параллельном переносе вниз, соответствующем изменению A, она коснётся заштрихованной области не в вершине , а в угловой точке около оси OX
   
9. 
   таким образом третье условие не влияет на результат, и для всех x > 0 и y > 0, удовлетворяющих условию 3y +2x  120, нужно обеспечить выполнение условия
   

y < – 2x +A

10. 
    умножим обе части последнего неравенства на 3: 3y < – 6x +3A
    
11. 
    теперь, учитывая, что 3y  –2x + 120, получаем, что максимальное значение 3y, которое нужно «перекрыть», равно –2x + 120
    
12. 
    поэтому получаем –2x + 120 < – 6x +3A или 3A > 120 + 4x
    
13. 
    максимально возможное значение x, удовлетворяющее условию 3y +2x  120, определяется подстановкой минимального y, равного 1: 3 +2x  120  2x  117  x_max = 58
    
14. 
    поэтому допустимые значение A определяются условием:
    

3A > 120 + 4x_max = 120 + 458 = 352

откуда следует, что A > 117,(6), то есть A_min = 118.

15. 
    Ответ: 118.
    

Ещё пример задания:

Р-29. Укажите наименьшее целое значение А, при котором выражение

(y + 2x < A) ∨ (x > 20) ∨ (y > 30)

истинно для любых целых положительных значений x и y.

Решение:

1. 
   второе и третье выражения не зависят от выбора A: (x > 20) or (y > 30)
   
2. 
   таким образом, нам нужно выбрать значение A так, чтобы условие (y + 2x < A)
   

выполнялось при всех x и y, для которых ложно (x > 20) or (y > 30), то есть истинно

(x  20) and (y  30)

3. 
   поскольку по условию x и y должны быть положительны, добавляем ещё два условия:
   

(x  20) and (y  30) and (x > 0) and (y > 0)

4. 
   изобразим схематично на плоскости x – y эту область (она заштрихована):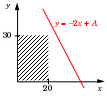
   

5. 
   для всех точек этой области должно выполняться условие y + 2x < A, равносильное условию
   

y < – 2x +A

6. 
   это значит, что вся область должна лежать ниже линии y = – 2x +A; одна такая подходящая линия показана на рисунке сверху
   
7. 
   очевидно, что минимальное значение A соответствует ситуации, когда при параллельном переносе показанной линии вниз, соответствующем изменению A, она коснётся правого верхнего угла заштрихованного прямоугольника, то есть пройдёт через точку (x = 20, y = 30)
   
8. 
   поэтому допустимые значение A определяются условием:
   

30 < – 220 +A

откуда следует, что A > 70, то есть A_min = 71.

9. 
   Ответ: 71.