Основные понятия математической логики

• Название: Основные понятия математической логики
• Дата: 02.02.2022
• Размер: 2.32 Mb.
• Имя файла: ege15.doc
• Тип: Закон; #349239
• страница: 8 из 50

Ещё пример задания:

Р-24. Введём выражение M & K, обозначающее поразрядную конъюнкцию M и K (логическое «И» между соответствующими битами двоичной записи). Определите наименьшее натуральное число a, такое что выражение

( (x & 28  0)  (x & 45  0))  ((x & 48 =0)  (x & a 0))

тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной x)?

Решение:

1. 
   Введём обозначения:
   

Z₂₈ = (x & 28 = 0), Z₄₅ = (x& 45 = 0), Z₄₈ = (x& 48 = 0), A = (x&a= 0)

2. 
   перепишем исходное выражение и преобразуем его, используя свойство импликации:
   

3. 
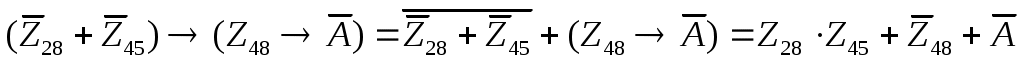
   перейдем к импликации, используя закон де Моргана:
   

4. 
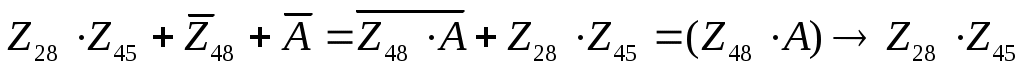
   преобразуем выражение в правой части по формуле 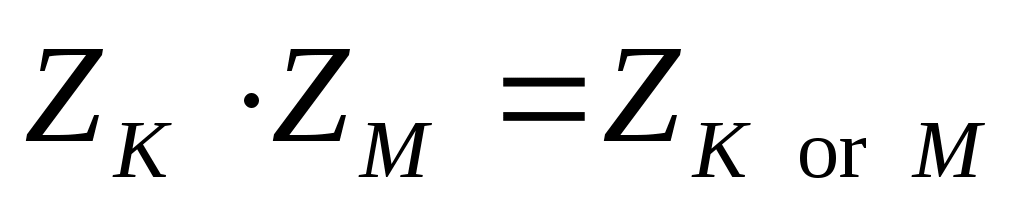, выполнив поразрядную дизъюнкцию (операцию ИЛИ):
   

28 = 011100

45 = 101101

28. 
    or 45 = 111101 = 61
    

получаем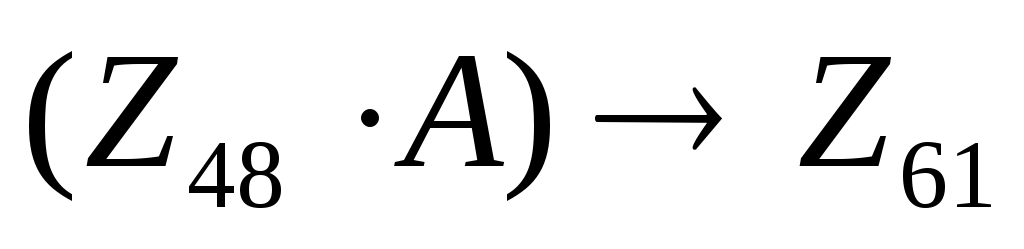

5. 
   для того, чтобы выражение 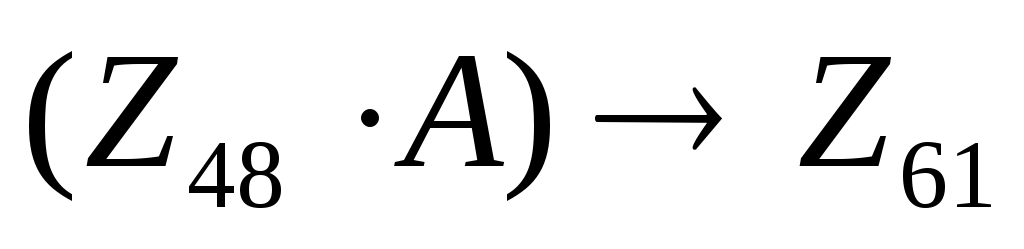было истинно для всех x, нужно, чтобы двоичная запись числа 48 or a содержала все единичные биты числа 61. Таким образом, с помощью числа a нужно добавить те единичные биты числа 61, которых «не хватает» в числе 48:
   

48 = 110000

a = **11*1

61 = 111101

биты, обозначенные звездочками, могут быть любыми.

6. 
   поскольку нас интересует минимальное значение a, все биты, обозначенные звездочкой, можно принять равными нулю.
   
7. 
   получается A = 2³ + 2² + 2⁰ = 13
   
8. 
   Ответ: 13.
   

Ещё пример задания (М.В. Кузнецова):

Р-23. Введём выражение M & K, обозначающее поразрядную конъюнкцию M и K (логическое «И» между соответствующими битами двоичной записи). Определите наибольшее натуральное число a, такое что выражение
(( (x & a  0)  (x & 12  0))  ((x & a =0)  (x & 21 0)))  ((x & 21  0)  (x & 12 =0))
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной X)?

Решение:

1. 
   Введём обозначения:
   

Z₁₂ = (X & 12 = 0), Z₂₁ = (X & 21 = 0), A = (X &a= 0)

2. 
   перепишем исходное выражение и преобразуем его, используя свойство импликации:
   

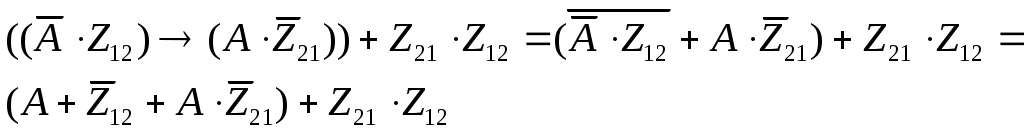
Выражение в первой скобке упрощаем, используя следствие из распределительного закона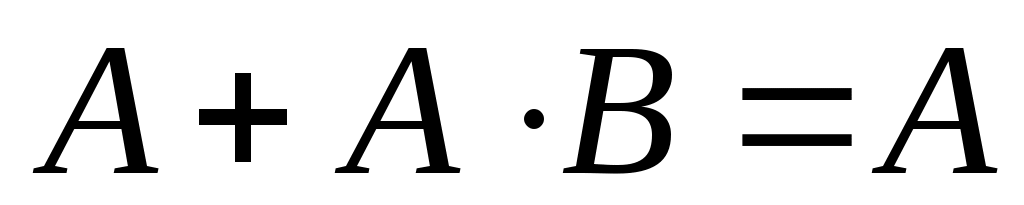



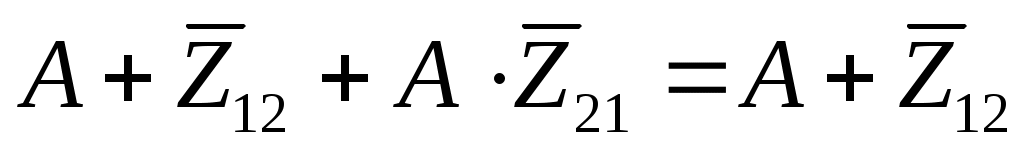
Полученное выражение также можно упростить, используя ещё одно следствие из распределительного закона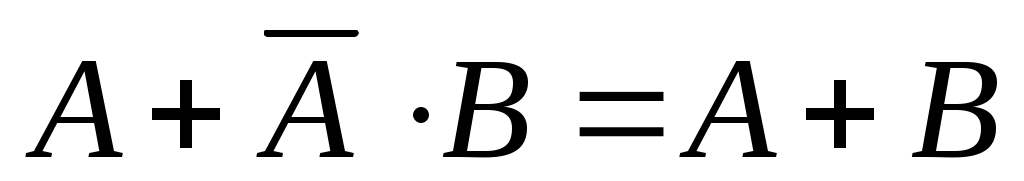

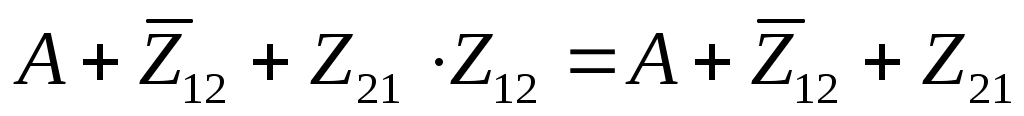
3. 
   перейдем к импликации, избавившись от инверсии:
   

4. 
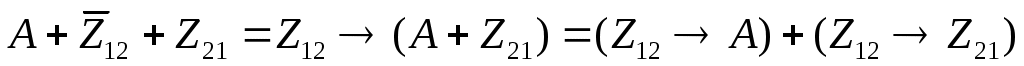
   поскольку множество единичных битов числа 21 = 10101­₂ не входит во множество единичных битов числа 12 = 1100­₂, импликация 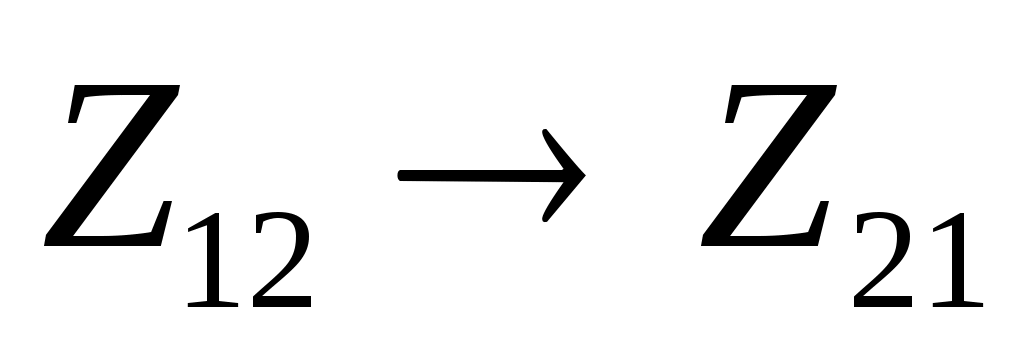ложна для некоторых x; поэтому нужно обеспечить истинность выражения
   
5. 
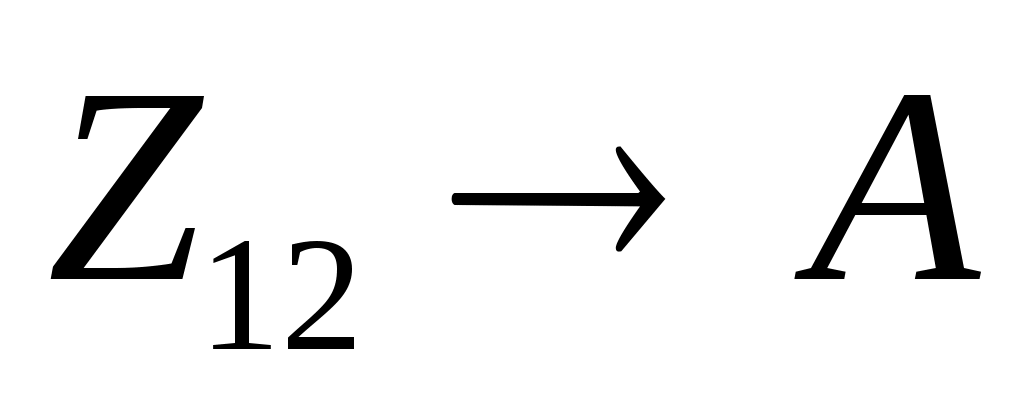
   выражение 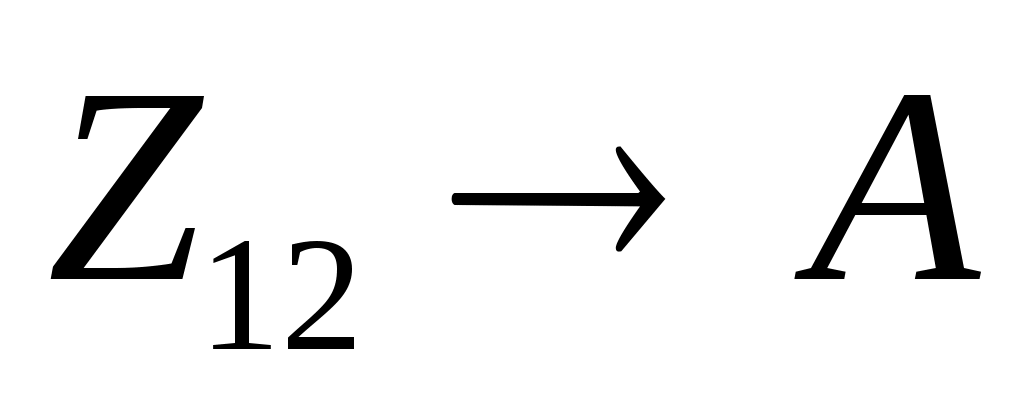истинно при условии, что множество единичных битов числа a входит во множество единичных битов числа 12, поэтому в двоичной записи числа a ненулевыми могут быть только биты в разрядах 2 и 3
   
6. 
   поэтому a_max = 2³ + 2² = 12.
   
7. 
   Ответ: 12.
   

Решение (программа на Python, Г.М. Федченко):

1. 
   программа на Python, полный перебор:
   

def f( x, a ):

return ( ((x & a != 0) and (x & 12 == 0)) <= \

((x & a == 0) and (x & 21 != 0)) ) or \

(x & 21 == 0) and (x & 12 == 0)

for a in range(1, 1000):

OK = True

for x in range(1,1000):

if not f(x, a):

OK = False

break

if OK:

print( a )

2. 
   вариант без функции:
   

for a in range(1, 1000):

OK = 1

for x in range(1,1000):

OK *= ( ((x & a != 0) and (x & 12 == 0)) <= \

((x & a == 0) and (x & 21 != 0)) ) or \

(x & 21 == 0) and (x & 12 == 0)

if not OK: break

if OK:

print( a )

3. 
   Ответ: 12.