Задачи. Решение задач Назмутдинов. Решение 1
 Скачать 78.86 Kb. Скачать 78.86 Kb.
|
|
Задание Найти пределы функций: 1) 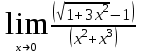 ; 2) ; 2) 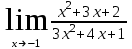 ; ; 3) 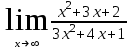 ; 4) ; 4) 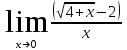 ; 5) ; 5) 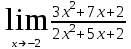 ; 6) ; 6) 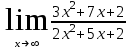 ; ; 7) 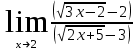 . .Решение: 1) 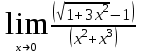 . .При подстановке вместо переменной значения 0, получим неопределенность вида 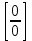 . Для раскрытия данной неопределенности, преобразуем выражение, стоящее под знаком предела, домножив числитель и знаменатель на выражение, сопряженное числителю: . Для раскрытия данной неопределенности, преобразуем выражение, стоящее под знаком предела, домножив числитель и знаменатель на выражение, сопряженное числителю: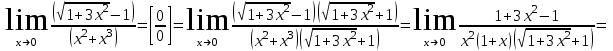 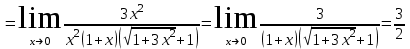 . .2) 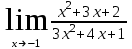 . .При подстановке вместо переменной значения -1, получим неопределенность вида 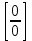 . Для раскрытия данной неопределенности, преобразуем выражение, стоящее под знаком предела, разложив числитель и знаменатель дроби на простые множители: . Для раскрытия данной неопределенности, преобразуем выражение, стоящее под знаком предела, разложив числитель и знаменатель дроби на простые множители: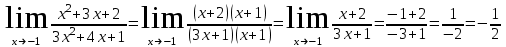 . . 3) 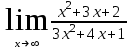 . .При подстановке вместо переменной значения 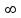 , получим неопределенность вида , получим неопределенность вида 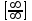 . Для раскрытия данной неопределенности, преобразуем выражение, стоящее под знаком предела, разделив числитель и знаменатель дроби на . Для раскрытия данной неопределенности, преобразуем выражение, стоящее под знаком предела, разделив числитель и знаменатель дроби на 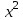 : :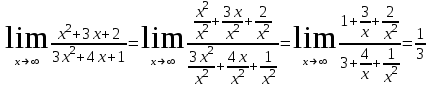 . .4) 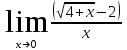 . .При подстановке вместо переменной значения 0, получим неопределенность вида 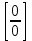 . Для раскрытия данной неопределенности, преобразуем выражение, стоящее под знаком предела, домножив числитель и знаменатель на выражение, сопряженное числителю: . Для раскрытия данной неопределенности, преобразуем выражение, стоящее под знаком предела, домножив числитель и знаменатель на выражение, сопряженное числителю: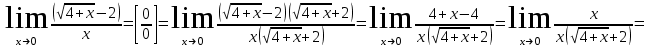 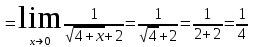 . .5) 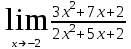 . .При подстановке вместо переменной значения -2, получим неопределенность вида 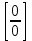 . Для раскрытия данной неопределенности, преобразуем выражение, стоящее под знаком предела, разложив числитель и знаменатель дроби на простые множители: . Для раскрытия данной неопределенности, преобразуем выражение, стоящее под знаком предела, разложив числитель и знаменатель дроби на простые множители: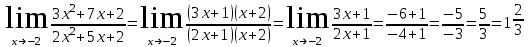 . . 6) 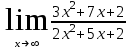 . .При подстановке вместо переменной значения 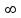 , получим неопределенность вида , получим неопределенность вида 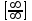 . Для раскрытия данной неопределенности, преобразуем выражение, стоящее под знаком предела, разделив числитель и знаменатель дроби на . Для раскрытия данной неопределенности, преобразуем выражение, стоящее под знаком предела, разделив числитель и знаменатель дроби на 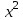 : :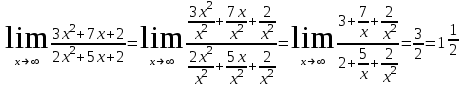 . .7) 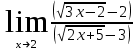 . .При подстановке вместо переменной значения 2, получим неопределенность вида 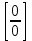 . Для раскрытия данной неопределенности, преобразуем выражение, стоящее под знаком предела, домножив числитель и знаменатель на выражение, сопряженное знаменателю, а затем на выражение, сопряженное числителю: . Для раскрытия данной неопределенности, преобразуем выражение, стоящее под знаком предела, домножив числитель и знаменатель на выражение, сопряженное знаменателю, а затем на выражение, сопряженное числителю: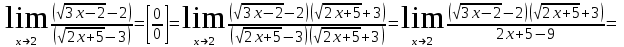 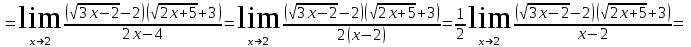 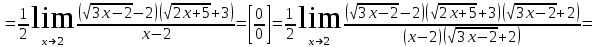 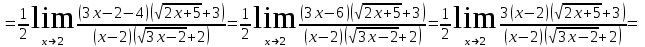 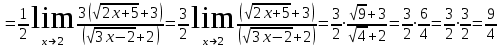 . .Ответ: 1) 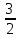 ; 2) ; 2) 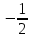 ; 3) ; 3) 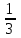 ; 4) ; 4) 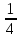 ; 5) ; 5) 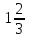 ; 6) ; 6) 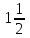 ; 7) ; 7) 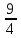 . . |
