Основные понятия, величины и законы теории электрических цепей
 Скачать 2.37 Mb. Скачать 2.37 Mb.
|
|
1.6. Элементы – накопители электромагнитной энергии 1.6.1. Индуктивный элемент Индуктивный элемент – двухполюсный элемент цепи, единственным процессом в котором является процесс запасания и возврата без потерь энергии магнитного поля. Описывается индуктивный элемент уравнением 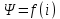 – вебер-амперной характеристикой, где – вебер-амперной характеристикой, где 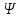 – потокосцепление самоиндукции элемента. Параметром элемента является индуктивность – потокосцепление самоиндукции элемента. Параметром элемента является индуктивность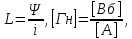 причем в общем случае  (см. п. 1.2). Напряжение элемента определяется скоростью изменения потокосцепления: (см. п. 1.2). Напряжение элемента определяется скоростью изменения потокосцепления: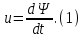 Отсюда ВАХ индуктивного элемента в общем случае такова: 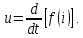 Индуктивный элемент с вебер-амперной характеристикой 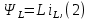 где 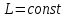 , условимся называть L-элементом. Его ВАХ в дифференциальной форме очевидно следует из формул (1) и (2): , условимся называть L-элементом. Его ВАХ в дифференциальной форме очевидно следует из формул (1) и (2):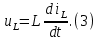 Обозначение L-элемента и его вебер-амперная характеристика приведены на рис. 1.21.  Рис. 1.21 Примечание. У реальных элементов – катушек индуктивности – характеристика отклоняется от линейной. Причина – зависимость магнитной проницаемости материала сердечника от тока; особенно она сильна у ферромагнетиков. Соответственно, нелинейный индуктивный элемент имеет сложную ВАХ: 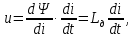 где 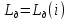 – дифференциальная индуктивность. – дифференциальная индуктивность.Проинтегрировав (3), получим ВАХ L-элемента в интегральной форме: 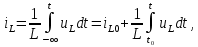 где 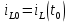 – начальный ток L-элемента. – начальный ток L-элемента.Энергия индуктивного элемента, согласно его определению, должна быть неотрицательной. Найдем энергию L-элемента: 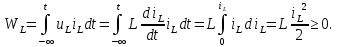 Простейшие эквивалентные преобразования. При последовательном соединении L-элементов эквивалентная индуктивность 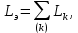 при параллельном 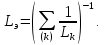 Из формулы (3) вытекает принцип непрерывности тока L-элемента: если напряжение L-элемента ограничено, то его ток непрерывен и не может измениться скачком, то есть для любого момента времени 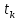 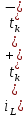 где 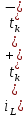 Докажем это от противного. Пусть в некоторый момент времени 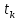 ток ток 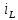 изменяется скачком на величину изменяется скачком на величину 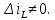 Тогда напряжение Тогда напряжение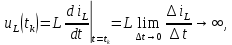 что противоречит исходному условию принципа. Принцип справедлив в общем случае для любого индуктивного элемента при условии непрерывности его вебер-амперной характеристики. 1.6.2. Емкостный элемент Емкостный элемент – двухполюсный элемент цепи, единственным процессом в котором является процесс запасания и возврата без потерь энергии электрического поля. Описывается емкостный элемент уравнением 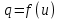 – кулон-вольтной характеристикой, где – кулон-вольтной характеристикой, где 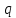 – заряд элемента. Параметром элемента является емкость – заряд элемента. Параметром элемента является емкость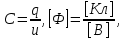 причем в общем случае 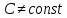 (см. п. 1.2). Ток элемента определяется скоростью изменения заряда: (см. п. 1.2). Ток элемента определяется скоростью изменения заряда: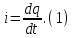 Отсюда ВАХ емкостного элемента в общем случае такова: 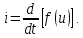 Емкостный элемент с кулон-вольтной характеристикой 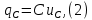 где 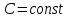 , условимся называть C-элементом. Его ВАХ в дифференциальной форме очевидно следует из формул (1) и (2): , условимся называть C-элементом. Его ВАХ в дифференциальной форме очевидно следует из формул (1) и (2):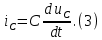 Обозначение С-элемента и его кулон-вольтная характеристика приведены на рис. 1.22.  Рис. 1.22 Примечание. У реальных элементов – конденсаторов – характеристика отклоняется от линейной. Причина – зависимость диэлектрической проницаемости материала разделительного слоя от напряжения; особенно она сильна у сегнетоэлектриков. Соответственно, нелинейный емкостный элемент имеет сложную ВАХ: 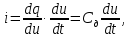 где 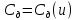 – дифференциальная емкость. – дифференциальная емкость.Проинтегрировав (3), получим ВАХ C-элемента в интегральной форме: 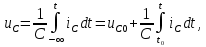 где 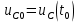 – начальное напряжение С-элемента. – начальное напряжение С-элемента.Энергия емкостного элемента, согласно его определению, должна быть неотрицательной. Найдем энергию С-элемента: 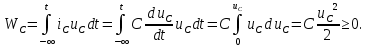 Простейшие эквивалентные преобразования. При последовательном соединении C-элементов эквивалентная емкость 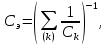 при параллельном 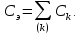 Из формулы (3) вытекает принцип непрерывности напряжения C-элемента: если ток C-элемента ограничен, то его напряжение непрерывно и не может измениться скачком, то есть для любого момента времени 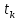 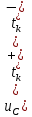 где 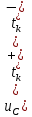 Докажем это от противного. Пусть в некоторый момент времени 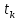 напряжение напряжение 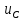 изменяется скачком на величину изменяется скачком на величину 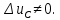 Тогда ток Тогда ток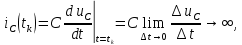 что противоречит исходному условию принципа. Принцип справедлив в общем случае для любого емкостного элемента при условии непрерывности его кулон-вольтной характеристики. 1.7. Элементы – источники электромагнитной энергии 1.7.1. Источник напряжения Источник напряжения (ИН) – двухполюсный элемент цепи, напряжение которого определено и не зависит от тока, протекающего через источник в процессе его работы. Такие ИН называют также независимыми ИН. Обозначение ИН приведено на рис. 1.23.  Рис. 1.23 Свойства ИН: 1) ИН может развивать неограниченную мощность; 2) внутреннее сопротивление ИН равно нулю; 3) ИН с напряжением 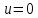 эквивалентен КЗ. эквивалентен КЗ.Режимы работы ИН. Рассмотрим схему на рис. 1.24.  Рис. 1.24 1. Режим ХХ – ключ К разомкнут, ИН отключен от нагрузки Н. 2. Режим нагрузки – ключ замкнут, напряжение нагрузки 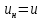 . .Примечание. Нагрузкой ИН может быть любой ДП за исключением элемента КЗ или другого ИН с напряжением 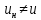 , так как в этом случае очевидно нарушается ЗНК. , так как в этом случае очевидно нарушается ЗНК.Уравнение (ВАХ) ИН. Для любого момента времени 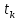 у ИН зависимость у ИН зависимость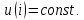 На рис. 1.25 приведен график ВАХ ИН для случая 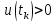 . . Рис. 1.25 Примечание. У реальных источников в режиме отдачи энергии ВАХ убывающая: с ростом тока, протекающего через источник, напряжение на его выводах снижается. Причина – наличие у источника ненулевого внутреннего сопротивления. Кроме того, ВАХ отклоняется от линейной. Соединение ИН. Соединение нескольких ИН не должно противоречить ЗНК. Например, параллельно ИН можно соединять только при одинаковой полярности и равенстве напряжений всех ИН. 1.7.2. Источник тока Источник тока (ИТ) – двухполюсный элемент цепи, ток которого определен и не зависит от напряжения, возникающего на выводах источника в процессе его работы. Такие ИТ называют также независимыми ИТ. Обозначение ИТ приведено на рис. 1.26.  Рис. 1.26 Свойства ИТ: 1) ИТ может развивать неограниченную мощность; 2) внутреннее сопротивление ИТ бесконечно велико; 3) ИТ с током 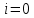 эквивалентен ХХ. эквивалентен ХХ.Режимы работы ИТ. Рассмотрим схему на рис. 1.27.  Рис. 1.27 1. Режим КЗ – ключ К замкнут, ИТ отключен от нагрузки Н. 2. Режим нагрузки – ключ разомкнут, ток нагрузки 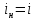 . .Примечание. Нагрузкой ИТ может быть любой ДП за исключением элемента ХХ или другого ИТ с током 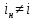 , так как в этом случае очевидно нарушается ЗТК. , так как в этом случае очевидно нарушается ЗТК.Уравнение (ВАХ) ИТ. Для любого момента времени 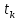 у ИТ зависимость у ИТ зависимость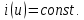 На рис. 1.28 приведен график ВАХ ИТ для случая 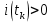 . .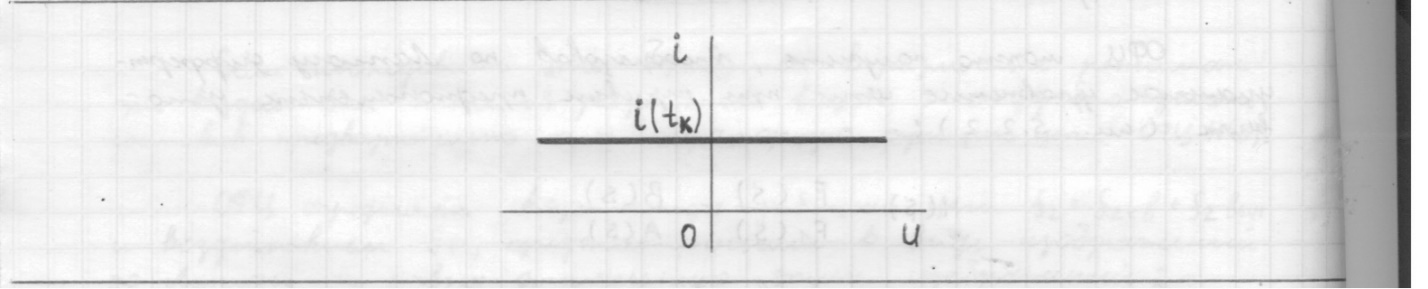 Рис. 1.28 Примечание. У реальных источников в режиме отдачи энергии ВАХ убывающая: с ростом напряжения на выводах источника отдаваемый ток уменьшается. Причина – наличие у источника конечного внутреннего сопротивления. Кроме того, ВАХ отклоняется от линейной. Соединение ИТ. Соединение нескольких ИТ не должно противоречить ЗТК. Например, последовательно ИТ можно соединять только при одинаковом направлении и равенстве токов всех ИТ. 1.7.3. Управляемые источники напряжения и тока Управляемый источник (УИ) – четырехполюсный элемент цепи, состоящий из пары ветвей, одна из которых – входная, или ветвь управления – представляет собой КЗ или ХХ, а другая – выходная – ИН или ИТ, причем напряжение ИН (ток ИТ) зависят от напряжения или тока ветви управления. Согласно определению, возможны четыре типа УИ: ИНУТ, ИНУН, ИТУТ, ИТУН. Их схемы в соответствующем порядке приведены на рис. 1.29.  Рис. 1.29 Описываются УИ уравнениями 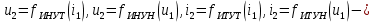 – передаточными характеристиками. Параметрами УИ являются, соответственно: сопротивление передачи 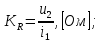 коэффициент передачи напряжения 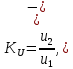 коэффициент передачи тока 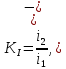 проводимость передачи 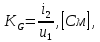 причем в общем случае 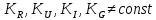 (см. п. 1.2). (см. п. 1.2).Свойства ИН и ИТ в составе УИ аналогичны свойствам независимых ИН и ИТ. Направление управляющего тока или полярность управляющего напряжения задаются на схеме цепи. Сама же ветвь управления обычно не изображается. Управляемые источники обладают свойством неограниченного усиления мощности сигналов. Рассмотрим произвольный УИ с подключенным к нему в качестве нагрузки R-элементом (см. рис. 1.30). 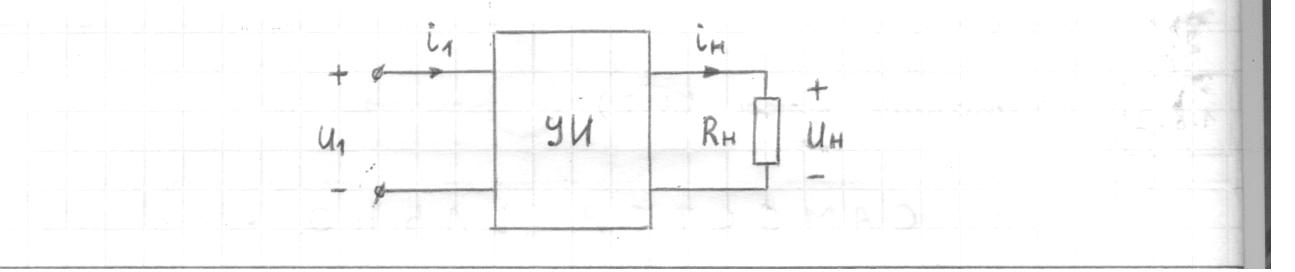 Рис. 1.30 Пусть 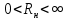 . Пусть управляющий сигнал УИ также отличен от нуля и ограничен. Тогда, в силу свойств КЗ и ХХ, входная мощность УИ . Пусть управляющий сигнал УИ также отличен от нуля и ограничен. Тогда, в силу свойств КЗ и ХХ, входная мощность УИ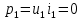 , ,мощность же нагрузки 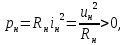 то есть 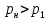 и и 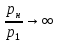 . .Управляемые источники относятся к классу активных элементов. Цепи с УИ называют активными цепями. Примечание. Реальными прототипами УИ являются, в частности, триоды, транзисторы, операционные усилители. 1.8. Дуальность элементов цепи и их характеристик Выпишем ВАХ RGLC-элементов, сгруппировав их попарно следующим образом: 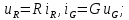 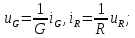 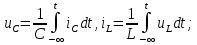 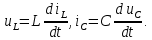 В каждой строке выражения имеют одинаковую структуру. При взаимной замене переменных 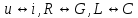 они переходят друг в друга. Такие выражения называются дуальными. Элементы, характеристики которых дуальны, называются дуальными элементами. Это элементы R и G, КЗ и ХХ, L и C, ИН и ИТ. Дуальны также их энергетические характеристики: 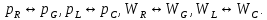 Кроме того, дуальными могут быть соединения, цепи и их уравнения. 1.9. Понятие о схемах замещения электротехнических устройств 1.9.1. Общие сведения Модель электротехнического устройства строится в виде его схемы замещения, составленной из идеализированных элементов. При этом одна часть элементов учитывает основные свойства оригинала, а другая – побочные, которые всегда имеют место из-за несовершенства материалов и конструкции. Первоначально схема может состоять только из одного элемента. Далее модель усложняется до тех пор, пока не будет достигнута требуемая степень ее соответствия оригиналу. Примеры схем замещения резистора, катушки индуктивности, конденсатора и источников питания (ИП) приведены в соответствующем порядке на рис. 1.31. 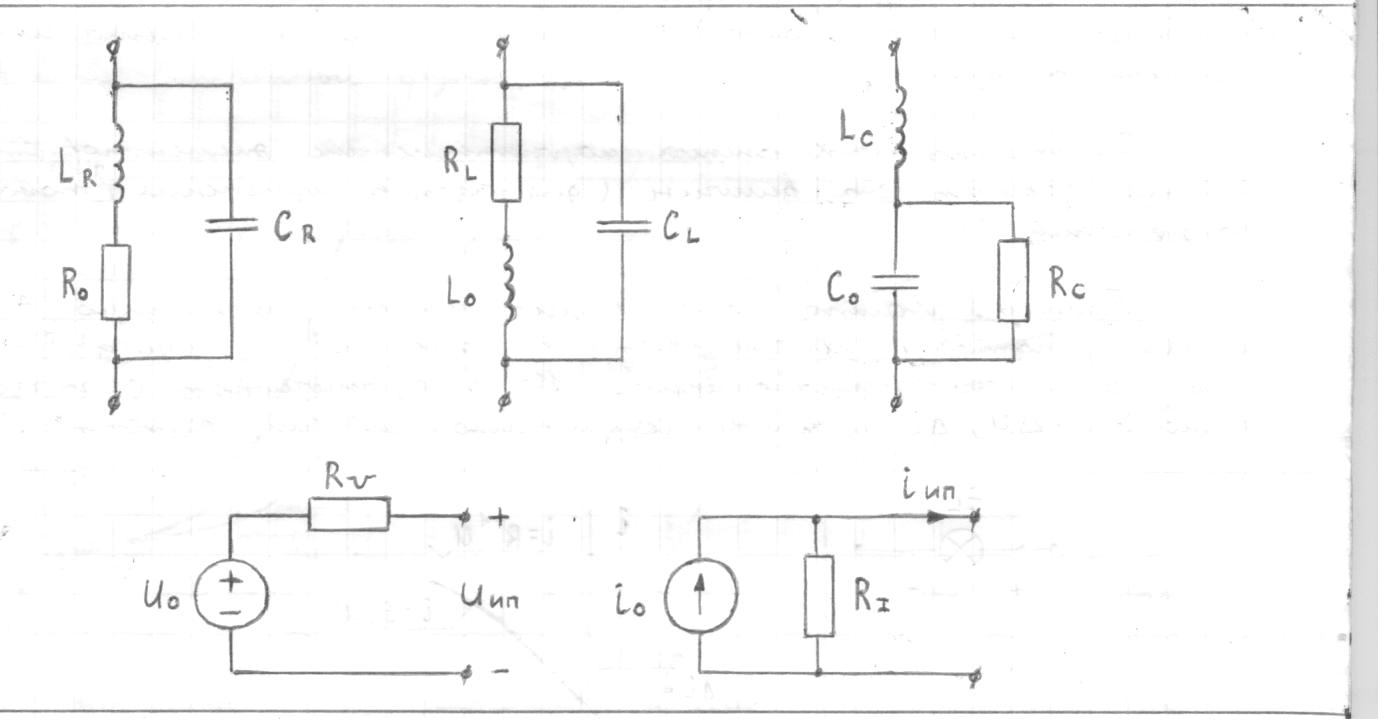 Рис. 1.31 На данных схемах: 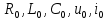 – элементы, учитывающие основные свойства устройств; – элементы, учитывающие основные свойства устройств; 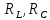 – сопротивления потерь в проводе катушки и диэлектрике конденсатора; – сопротивления потерь в проводе катушки и диэлектрике конденсатора; 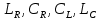 – паразитные индуктивность и емкость; – паразитные индуктивность и емкость; 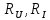 – внутренние сопротивления источников. – внутренние сопротивления источников.Одно и то же устройство может иметь несколько разных схем замещения. Обычно это связано с различными режимами его работы и объясняется следующим. Первое. Величины токов и напряжений в динамической цепи зависят, помимо всего прочего, от частоты сигналов. Рассмотрим, например, С-элемент с емкостью 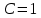 , к которому приложено переменное напряжение единичной амплитуды и частоты: , к которому приложено переменное напряжение единичной амплитуды и частоты: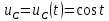 . .Найдем ток элемента: 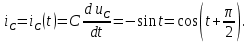 Не изменяя амплитуды напряжения, увеличим его частоту, например, в 10 раз: 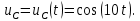 Величина тока десятикратно возрастает: 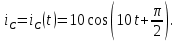 Таким образом, влияние паразитных параметров на разных частотах неодинаково. В одном диапазоне частот оно может быть пренебрежимо малым, а в другом, напротив, весьма существенным. Соответственно, схемы замещения устройства на разных частотах тоже, как правило, различны. Второе. Все реальные устройства нелинейны, и далеко не каждое можно заместить линейной моделью без потери каких-либо принципиальных качеств оригинала. Но даже если такая замена возможна, то обычно только для некоторого ограниченного динамического диапазона (интервала изменения токов и напряжений). 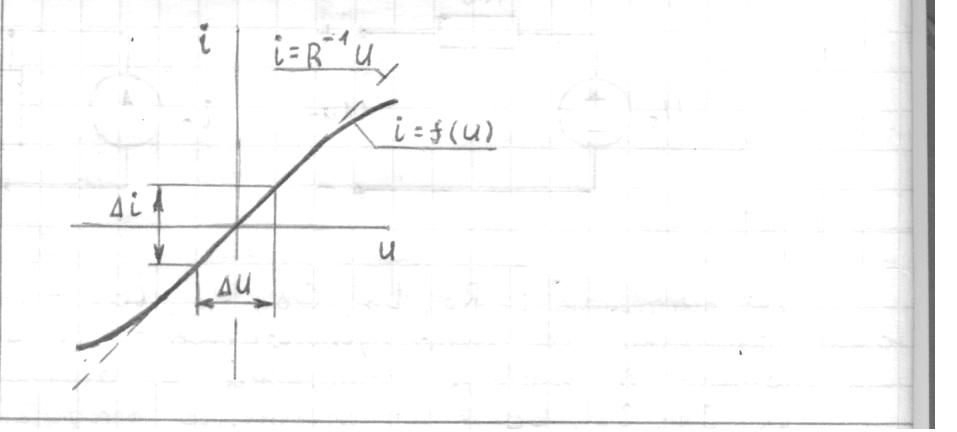 Рис. 1.32 В качестве иллюстрации на рис. 1.32 приведены две ВАХ: нелинейная – устройства-оригинала и линейная – модели. Очевидно, что степень соответствия модели оригиналу в различных интервалах 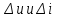 будет различной. будет различной.Вывод: одно и то же устройство может иметь линейную модель в одном динамическом диапазоне и нелинейную – в другом. Принимая в расчет какую-либо модель электротехнического устройства, необходимо учитывать, для какого частотного или динамического диапазона она построена. Использование неадекватной модели может привести к получению результатов, не соответствующих действительности не только количественно, но и качественно. |
