Основные понятия, величины и законы теории электрических цепей
 Скачать 2.37 Mb. Скачать 2.37 Mb.
|
|
Глава 1. ОСНОВНЫЕ ПОНЯТИЯ, ВЕЛИЧИНЫ И ЗАКОНЫ ТЕОРИИ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ 1.1. Понятие об электрической цепи и ее элементах. Задача анализа цепи Электрическая цепь – теоретическая модель электротехнического устройства, предназначенная для описания электромагнитного процесса в нем с помощью понятий «электрический ток» и «электрическое напряжение». Электрическая цепь состоит из отдельных частей – элементов цепи. Это идеализированные устройства, которые отображают различные стороны электромагнитного процесса: генерацию, передачу, запасание-возврат, потребление электромагнитной энергии. Между собой элементы соединяются с помощью идеальных проводников тока – выводов. Все элементы цепи имеют строгое математическое описание и графическое обозначение. В общем случае элементы, а также отдельные участки цепи обычно изображают в виде прямоугольников. По количеству выводов элементы цепи подразделяются на двухполюсные (с двумя выводами) и четырехполюсные (с четырьмя выводами) – см. рис. 1.1. Соотношения, связывающие токи и напряжения на выводах, называют уравнениями или характеристиками элемента, а коэффициенты в них – параметрами элемента. 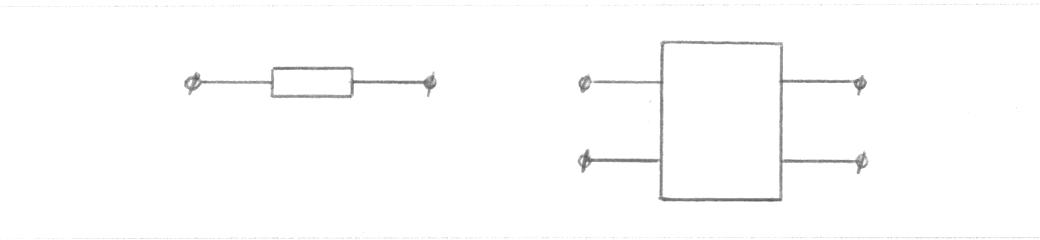 Рис. 1.1 Задачу анализа цепи сформулируем так. Заданы: 1) схема цепи (графическое изображение цепи в виде соединения элементов); 2) характеристики и параметры всех элементов цепи; 3) воздействия (входные сигналы) – токи и/или напряжения, подаваемые на цепь от внешних источников. Требуется найти реакции цепи (выходные сигналы) – токи и/или напряжения на выводах каких-либо элементов или участков цепи. Выводы, на которые подается воздействие, будем называть входом цепи, выводы, с которых снимается реакция – выходом цепи. 1.2. Классификация элементов цепи. Типы цепей Классифицируем элементы цепи по следующим критериям. 1. Критерий: содержание электромагнитного процесса. Элементы: - источники (учитывают преобразование энергии неэлектрической природы в электромагнитную); - накопители (учитывают запасание и возврат электромагнитной энергии без потерь); - потребители (учитывают преобразование электромагнитной энергии в другие виды энергии). 2. Критерий: наличие (а) или отсутствие (б) зависимости параметров элемента от следующих факторов. 2.1. Фактор: ток или напряжение на выводах. Элементы: а) нелинейные; б) линейные. 2.2. Фактор: время. Элементы: а) нестационарные (с переменными параметрами); б) стационарные (с постоянными параметрами). 2.3. Фактор: пространственные координаты. Элементы: а) с распределенными параметрами; б) с сосредоточенными параметрами. 3. Критерий: наличие (а) или отсутствие (б) у элемента свойства усиления мощности. Элементы: а) активные; б) пассивные. Цепи, состоящие только из источников и потребителей энергии, называют резистивными. Если же в цепи есть хотя бы один накопитель энергии, ее называют динамической. Кроме того, если в цепи действует хотя бы один элемент пункта «а» классификации, цепь также получает соответствующее этому пункту название, если нет – название дается по пункту «б». И резистивные, и динамические цепи могут, таким образом, быть линейными и нелинейными, активными и пассивными и т. д. 1.3. Основные понятия топологии цепей 1.3.1. Детали структуры цепей При соединении элементов цепи друг с другом образуются детали структуры цепи – узлы, ветви, контуры, ячейки. Узел – точка соединения выводов элементов. Соединение двух выводов образует простейший или устранимый узел (на рис. 1.2 узел а). На схемах цепей такие узлы, как правило, не изображаются. Соединение трех и более выводов образует неустранимый узел (на рис. 1.2 узел б). На схемах цепей неустранимые узлы изображаются в обязательном порядке. 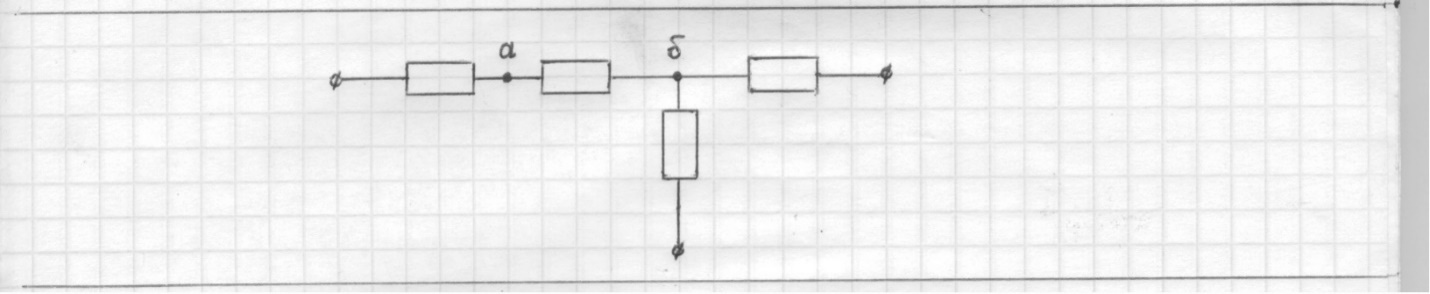 Рис. 1.2 Ветвь – в общем случае любая часть цепи, соединяющая два узла двумя выводами (см. рис. 1.3).  Рис. 1.3 Примечание. Понятие «ветвь» является понятием обобщающим. При анализе за ветви цепи можно принимать как отдельные ее элементы, так и целые соединения элементов. Контур – в общем случае любая часть цепи в виде кольцевого пути из ветвей и узлов, причем при обходе контура эти ветви и узлы не повторяются. Ячейка – контур без внутренних пересечений другими (не входящими в него) ветвями. Простейшая ячейка образуется соединением двух элементов.  Рис. 1.4 В цепи на рис. 1.4 цифрами 1, 2, 3 обозначены ячейки (ячейка 1 – простейшая), а кольцевыми стрелками – направление их обхода. Общее же число контуров в данной цепи равно 6; ввиду простоты схемы это легко определяется визуально. 1.3.2. Виды соединений двухполюсников Двухполюсник (ДП) – цепь (часть цепи, элемент) с двумя выводами (см. рис. 1.5).  Рис. 1.5 Последовательное соединение: ДП соединяются один за другим с образованием между соседними ДП только устранимых узлов (см. рис. 1.6).  Рис. 1.6 Последовательное соединение транзитивно: если ДП1 соединен последовательно с ДП2, а ДП2 – последовательно с ДП3, то ДП1 и ДП3 соединены последовательно. Параллельное соединение: ДП присоединяются к одной и той же паре узлов с образованием между соседними ДП только простейших ячеек (см. рис. 1.7). Параллельное соединение также транзитивно. 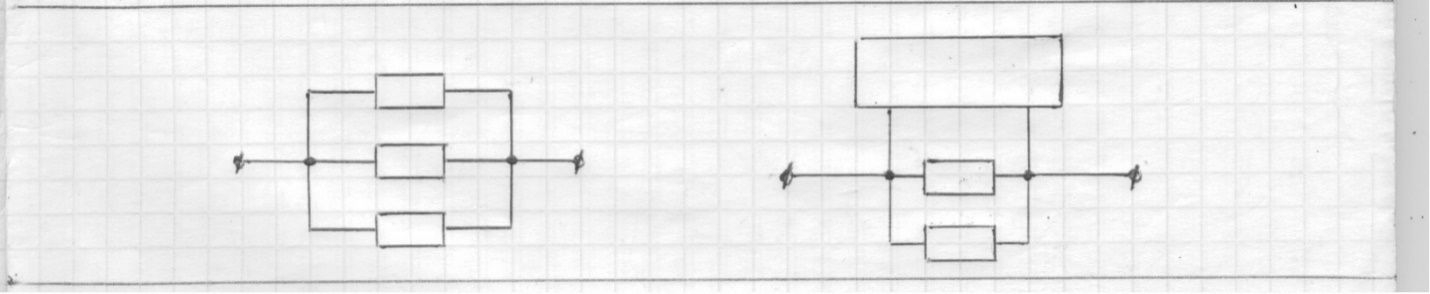 Рис. 1.7 Соединение n-лучевой звездой. Выводы n ДП соединяются по одному от каждого ДП в общем неустранимом узле, другие же их выводы общих узлов не имеют. На рис. 1.8 показано соединение ДП трехлучевой звездой. 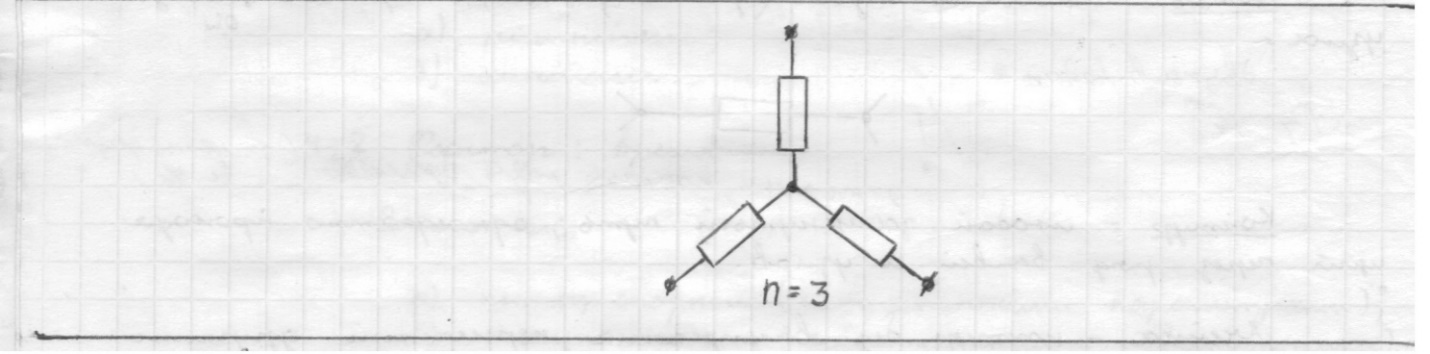 Рис. 1.8 Соединение n-угольником. Из n ДП образуется n-угольник с неустранимыми узлами в вершинах. На рис. 1.9 показано соединение ДП треугольником. 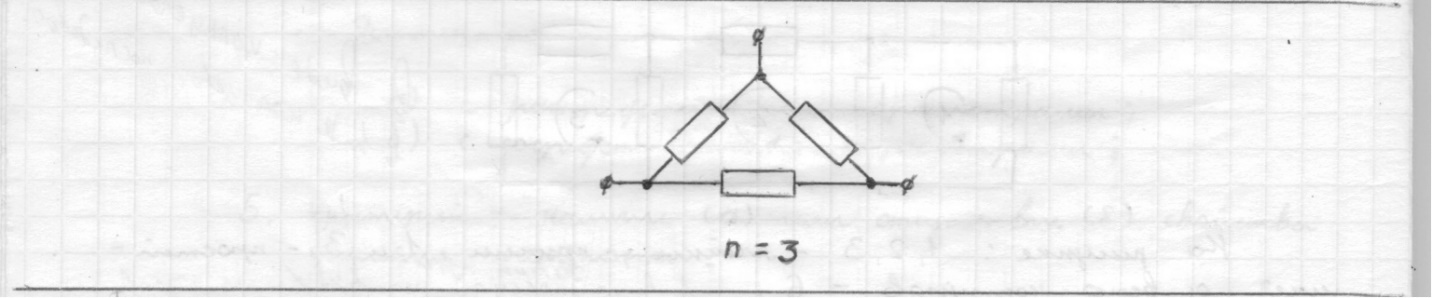 Рис. 1.9 На основе этих базовых соединений образуются: последовательно-параллельное (рис. 1.10),  Рис. 1.10 лестничное (рис. 1.11),  Рис. 1.11 мостовое (рис. 1.12)  Рис. 1.12 и другие соединения. 1.3.3. Понятие графа цепи Граф цепи – совокупность точек (узлов) и линий (ветвей), отображающая структурные свойства цепи. Если граф может быть изображен на плоскости без пересечения ветвей, он называется планарным, если нет – непланарным. На рис. 1.13а показан планарный граф (пересечение ветвей можно устранить – см. пунктир), а на рис. 1.13б – непланарный граф.  Рис. 1.13 Деталь графа, в которой все его узлы связаны между собой, но без образования контуров, называется деревом. Ветви, которые нужно удалить из графа для выделения дерева, называются ветвями связи или хордами. 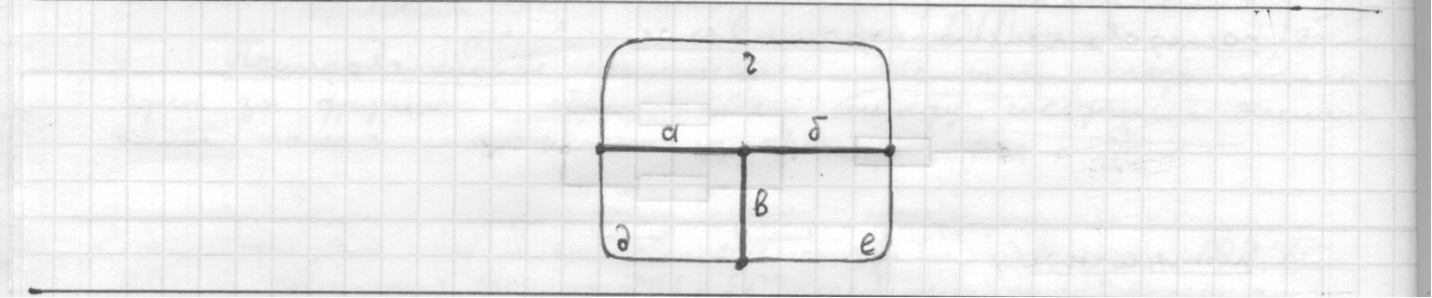 Рис. 1.14 На рис. 1.14: а, б, в – ветви дерева; г, д, е – ветви связи. 1.4. Ток, напряжение, мощность и энергия в цепи. Законы Кирхгофа 1.4.1. Ток и напряжение на участке цепи Пусть на некотором двухполюсном участке цепи (см. рис. 1.15) между точками 1 и 2 в течении времени 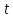 за счет энергии за счет энергии 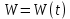 происходит направленный перенос электрического заряда происходит направленный перенос электрического заряда 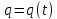 . Тогда говорят о наличии на этом участке электрического тока . Тогда говорят о наличии на этом участке электрического тока 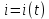 и электрического напряжения и электрического напряжения 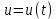 . . Рис. 1.15 Величина электрического тока определяется величиной заряда, который переносится в единицу времени через поперечное сечение проводника. Величина электрического напряжения определяется величиной энергии, необходимой для переноса единицы заряда из одной точки в другую. Полагая заряд и энергию непрерывными, определим (постулируем) ток и напряжение на участке цепи: 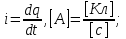 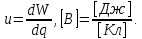 Однозначно определить ток и напряжение как функции времени можно, лишь указав предварительно направление тока и полярность напряжения. Направление тока указывают произвольно, стрелкой или индексами; при этом предполагают, что в данном направлении перемещаются носители положительных зарядов. Полярность напряжения указывают также произвольно, обычно знаками «+» и «–» или индексами; при этом предполагают, что у точки, отмеченной знаком «+», потенциал выше, чем у точки, отмеченной знаком «–». Направление тока и полярность напряжения на участке цепи называют согласованными, если ток внутри участка направлен от знака «+» к знаку «–» (см. рис. 1.15). 1.4.2. Мощность и энергия участка цепи Пусть ток и напряжение на участке цепи согласованы. Из формул п. 1.4.1 найдем: 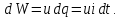 Мощность равна скорости изменения энергии. Найдем мощность участка цепи: 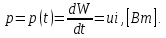 Если 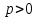 , то есть , то есть 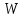 возрастает, участок забирает энергию; если возрастает, участок забирает энергию; если 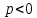 , то есть , то есть 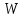 убывает – отдает энергию. убывает – отдает энергию.Согласно закону сохранения энергии сумма мощностей всех участков (элементов) цепи равна нулю, то есть соблюдается баланс мощностей: 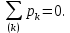 Примечание. Если ток и напряжение на участке цепи не согласованы, мощность 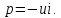 Найдем энергию участка цепи: 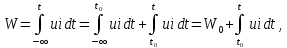 где 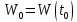 – начальная энергия участка, а – начальная энергия участка, а 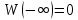 . .Если 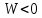 – на участке происходит генерация энергии, если – на участке происходит генерация энергии, если 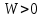 – потребление, запасание или возврат ранее запасенной энергии. – потребление, запасание или возврат ранее запасенной энергии.1.4.3. Законы (постулаты) Кирхгофа Закон токов Кирхгофа (ЗТК). Алгебраическая сумма токов ветвей, сходящихся в узле цепи, в любой момент времени равна нулю. Условимся для определенности: токи, втекающие в узел, брать со знаком «–», а вытекающие из узла – со знаком «+». 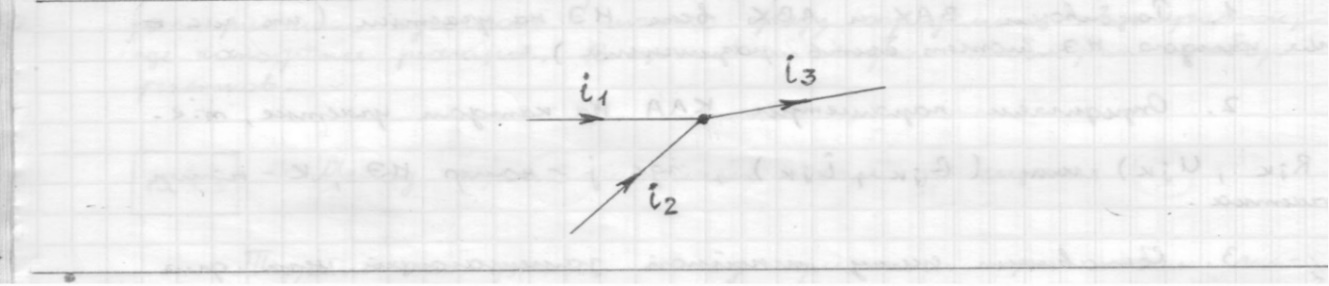 Рис. 1.16 Пример. Запишем уравнение Кирхгофа для узла на рис. 1.16: 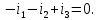 Закон напряжений Кирхгофа (ЗНК). Алгебраическая сумма напряжений ветвей, образующих контур цепи, в любой момент времени равна нулю. 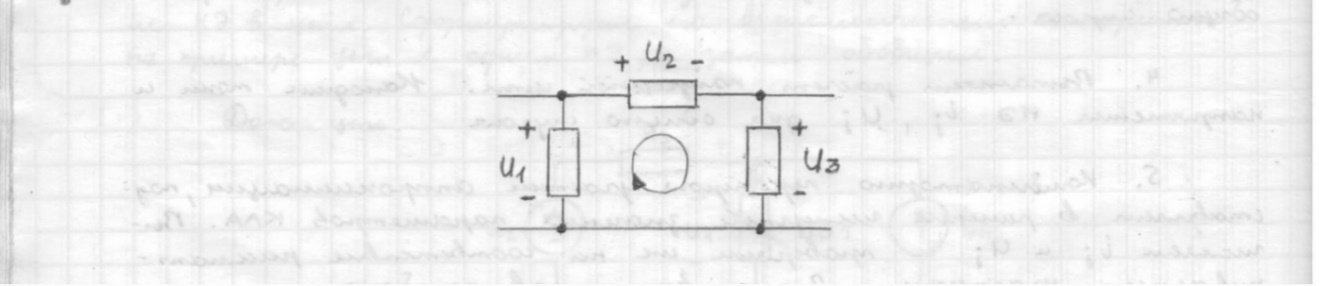 Рис. 1.17 Условимся для определенности: напряжение ветви брать со знаком «+», если при обходе контура мы проходим эту ветвь от вывода «+» к выводу «–» (и, соответственно, наоборот). Пример. Запишем уравнение Кирхгофа для контура на рис. 1.17: 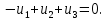 Следствия. 1. Ток последовательно соединенных элементов одинаков по величине, а при одинаково выбранном направлении – и по знаку. 2. Напряжение параллельно соединенных элементов одинаково по величине, а при одинаково выбранной полярности – и по знаку. 3. Перемена элементов местами не изменяет свойств последовательного и параллельного соединений. 1.5. Элементы – потребители электромагнитной энергии 1.5.1. Резистивный элемент Резистивный элемент – двухполюсный элемент цепи, единственным процессом в котором является процесс безвозвратного потребления электромагнитной энергии. Описывается резистивный элемент уравнением 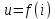 , или же уравнением , или же уравнением 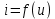 – вольт-амперной характеристикой (ВАХ). Параметром элемента является сопротивление – вольт-амперной характеристикой (ВАХ). Параметром элемента является сопротивление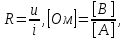 причем в общем случае 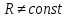 (см. п. 1.2). Величина, обратная сопротивлению, называется проводимостью: (см. п. 1.2). Величина, обратная сопротивлению, называется проводимостью: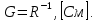 Резистивный элемент с ВАХ, определяемой законом Ома 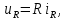 где 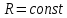 , условимся называть R-элементом. Обозначение R-элемента и его ВАХ приведены на рис. 1.18. , условимся называть R-элементом. Обозначение R-элемента и его ВАХ приведены на рис. 1.18. Рис. 1.18 Примечание. У реальных элементов – резисторов – ВАХ отклоняется от линейной. Причина – зависимость сопротивления резистора от температуры, то есть, соответственно, от тока. Мощность резистивного элемента, согласно его определению, должна быть неотрицательной. Найдем мощность R-элемента: 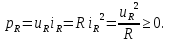 Простейшие эквивалентные преобразования. При последовательном соединении R-элементов эквивалентное сопротивление 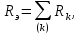 при параллельном 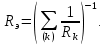 1.5.2. Условные потребители энергии – элементы короткого замыкания и холостого хода Элементом короткого замыкания (КЗ) называется R-элемент с сопротивлением 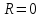 . Обозначение КЗ и его ВАХ приведены на рис. 1.19. . Обозначение КЗ и его ВАХ приведены на рис. 1.19.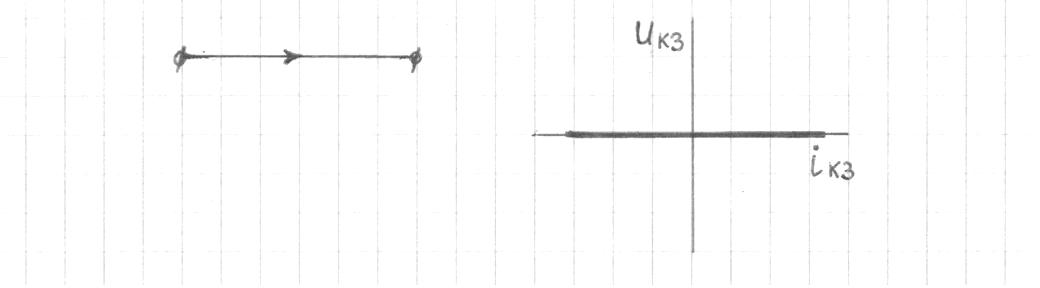 Рис. 1.19 Свойства КЗ: 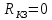 ; ; 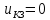 ; ; 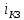 определяется внешней цепью. определяется внешней цепью.Элементом холостого хода (ХХ) называется R-элемент с сопротивлением 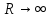 . Обозначение ХХ и его ВАХ приведены на рис. 1.20. . Обозначение ХХ и его ВАХ приведены на рис. 1.20.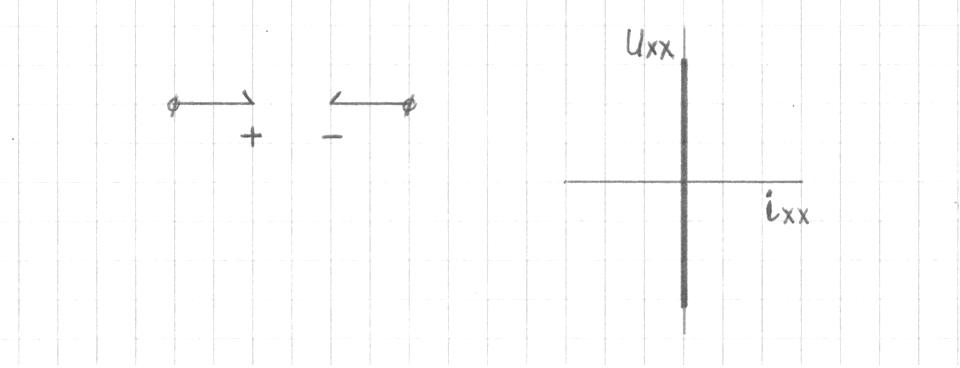 Рис. 1.20 Свойства ХХ: 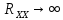 ; ; 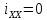 ; ; 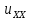 определяется внешней цепью. определяется внешней цепью.К потребителям энергии элементы КЗ и ХХ можно отнести лишь условно, так как мощности 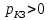 и и 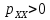 возможны лишь при возможны лишь при 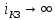 и и 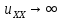 . . |
