Основные понятия, величины и законы теории электрических цепей
 Скачать 2.37 Mb. Скачать 2.37 Mb.
|
|
1.9.2. Пример построения линейной модели двухполюсного электротехнического устройства по его ВАХ Исходные данные. Замещаемое устройство – полупроводниковый стабилитрон. Предполагаемый режим работы – стабилизация постоянного напряжения. На рис 1.33а приведено обозначение стабилитрона с указанными направлением тока 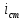 и полярностью напряжения и полярностью напряжения 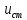 , а на рис. 1.33б – его ВАХ. , а на рис. 1.33б – его ВАХ.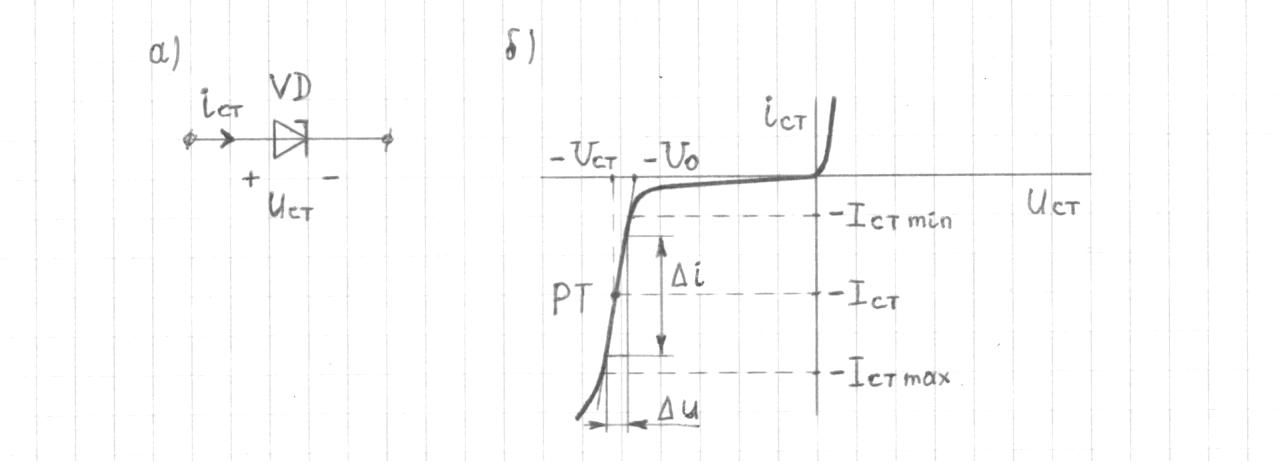 Рис. 1.33 Из графика видно, что стабилитрон – устройство нелинейное. В третьем квадранте его ВАХ имеет круто спадающий участок, напряжение на котором при 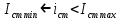 изменяется сравнительно слабо. На данном участке располагается точка с координатами изменяется сравнительно слабо. На данном участке располагается точка с координатами 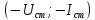 – так называемая рабочая точка (РТ). Проведем через РТ касательную до ее пересечения с осью абсцисс и запишем уравнение полученной прямой: – так называемая рабочая точка (РТ). Проведем через РТ касательную до ее пересечения с осью абсцисс и запишем уравнение полученной прямой: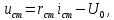 (1) (1)где 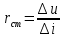 – дифференциальное сопротивление стабилитрона в рабочей точке, определяемое через малые приращения напряжения и тока в ее окрестности. – дифференциальное сопротивление стабилитрона в рабочей точке, определяемое через малые приращения напряжения и тока в ее окрестности.Учитывая, что в исследуемом режиме потенциал катода стабилитрона выше, чем потенциал анода (такое включение устройства называют обратным), изменим на схеме направление тока и полярность напряжения на противоположные (см. рис. 1.34а). Рассматриваемый участок ВАХ перейдет при этом в первый квадрант. Соответственно, изменится и уравнение (1): 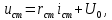 (2) (2)где 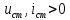 . .Составим согласно уравнению (2) схему замещения стабилитрона (см. рис. 1.34б). 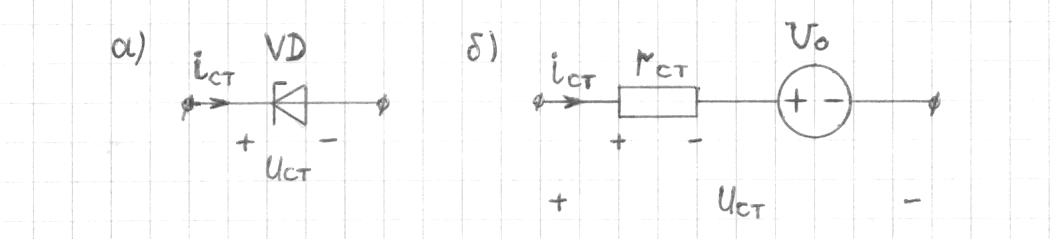 Рис. 1.34 1.9.3. Пример построения линейной модели четырехполюсного электротехнического устройства по его ВАХ Исходные данные. Замещаемое устройство – биполярный транзистор типа n–p–n, включенный по схеме с общим эмиттером (см. рис. 1.35). Предполагаемый режим работы – линейное усиление переменного сигнала.  Рис. 1.35 На рис. 1.35 буквами обозначены выводы транзистора: «б» – база, «к» – коллектор, «э» – эмиттер; 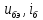 – входные, а – входные, а 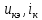 – выходные переменные. Обратимся к характеристикам транзистора (см. рис. 1.36). – выходные переменные. Обратимся к характеристикам транзистора (см. рис. 1.36).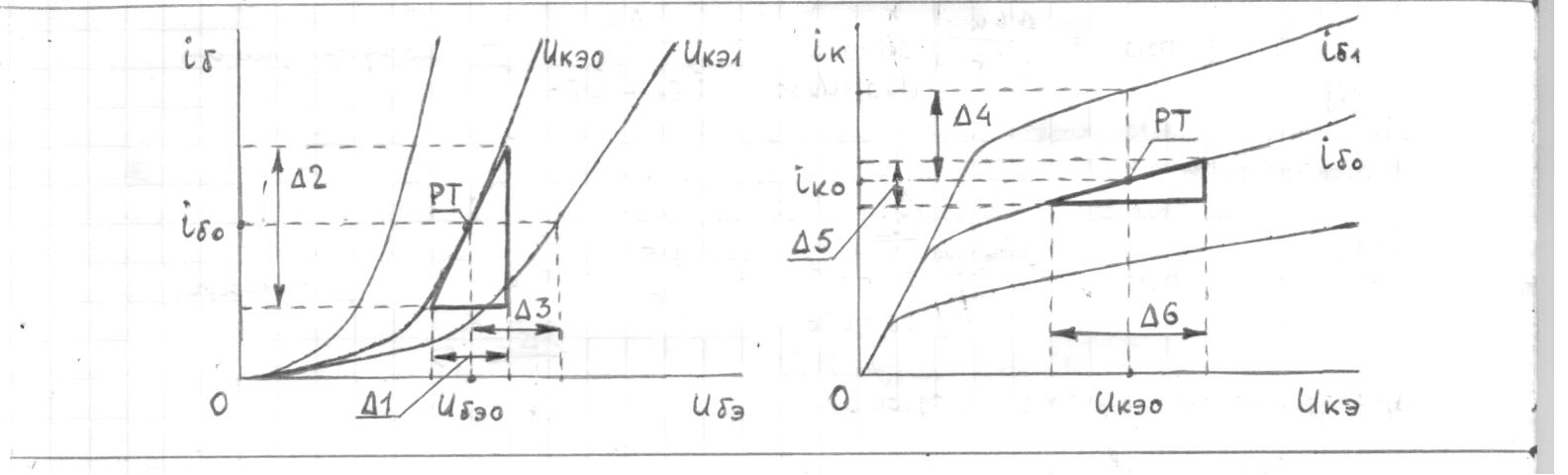 Рис. 1.36 Из графиков видно, что транзистор – устройство нелинейное. Однако, задавая определенным образом режим его работы при постоянных токах и напряжениях 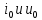 – рабочую точку РТ и ограничивая диапазоны изменения сигналов – рабочую точку РТ и ограничивая диапазоны изменения сигналов 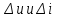 в ее окрестности, то есть полагая в ее окрестности, то есть полагая 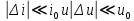 , линейную модель построить можно. , линейную модель построить можно.Установим связь между токами и напряжениями транзистора в такой, например, форме: 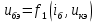 ; ;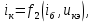 где 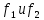 – линейные функции. – линейные функции.Представим каждый ток и напряжение в виде суммы двух составляющих: постоянной (определяемой РТ) и малой переменной: 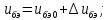 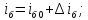 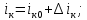 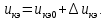 Заменим характеристики в окрестности РТ касательными и запишем линейные уравнения относительно только переменных составляющих: 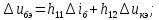 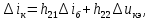 где 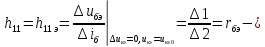 – входное сопротивление транзистора; 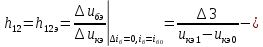 – коэффициент обратной передачи напряжения; 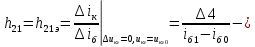 – коэффициент передачи тока; 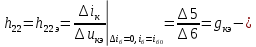 – выходная проводимость транзистора. Обозначим 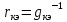 и составим согласно полученным линейным уравнениям схему замещения транзистора (см. рис. 1.37). и составим согласно полученным линейным уравнениям схему замещения транзистора (см. рис. 1.37).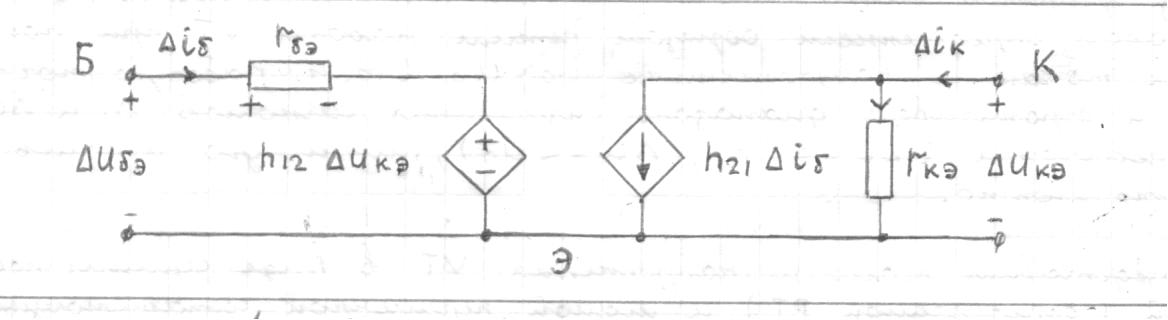 Рис. 1.37 Примечание. Коэффициенты 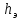 называют малосигнальными параметрами транзистора в схеме с общим эмиттером. Находят их графически или экспериментально. Иногда транзистор считают идеальным и принимают называют малосигнальными параметрами транзистора в схеме с общим эмиттером. Находят их графически или экспериментально. Иногда транзистор считают идеальным и принимают – КЗ, – КЗ,  – КЗ, – КЗ,  – ХХ; – ХХ;схема замещения превращается тогда в схему ИТУТ. В заключение отметим, что полученная схема никак не учитывает частотных свойств оригинала и может использоваться только в области относительно низких частот. 1.10. Описание цепи системой линейно независимых уравнений Кирхгофа Во многих случаях задача анализа требует описания исследуемой цепи системой независимых уравнений относительно каких-либо токов и/или напряжений, выбранных в качестве искомых переменных. Изложим методику составления такой системы на примере анализа конкретной цепи. Сделаем предварительные замечания. Из определения ИН и ИТ следует, что для ИН всегда неизвестен ток, а для ИТ – напряжение. Для всех остальных элементов неизвестны и ток, и напряжение, но одна из этих двух величин является зависимой. Таким образом, число N искомых переменных (и, соответственно, размерность формируемой системы уравнений) в общем случае равны числу элементов цепи. Примечание. Для уменьшения размерности системы в качестве искомых переменных часто выбирают токи и/или напряжения ветвей цепи (см. п. 1.3.1). В этом случае для каждой ветви вначале составляют ее уравнение – ВАХ. Рассмотрим цепь, для простоты – резистивную (см. рис. 1.38а). Опишем цепь системой линейно независимых уравнений Кирхгофа. Условимся каждый элемент цепи считать ветвью. Обозначим на схеме все узлы и контуры, укажем направления искомых токов и полярности искомых напряжений. Построим граф цепи, в котором сплошными линиями выделим ветви дерева, а пунктирными – ветви связи (см. рис. 1.38б). 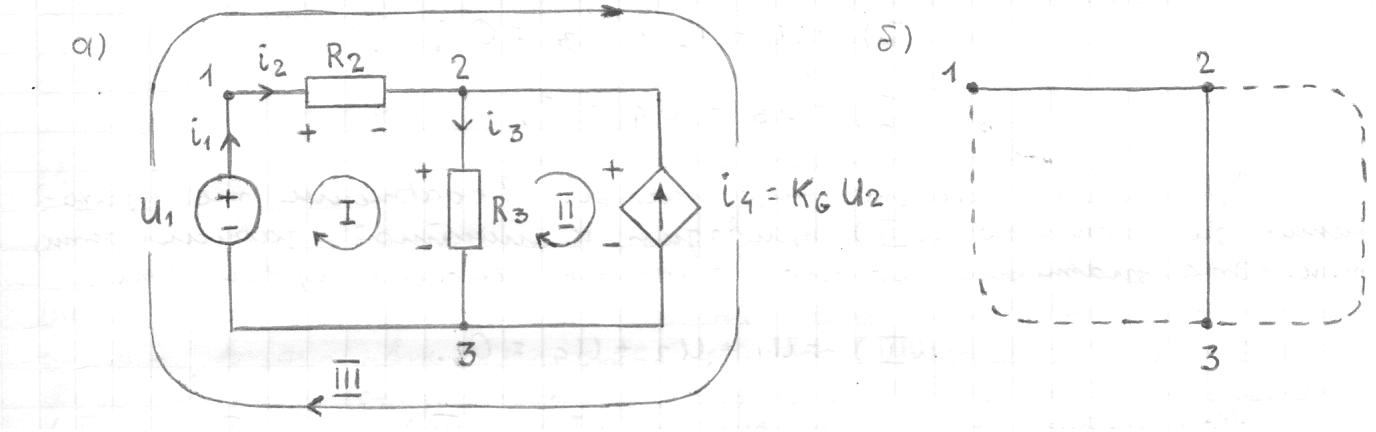 Рис. 1.38 Утверждение 1 (принимаем без доказательства). Максимальное число независимых уравнений, которые можно составить по ЗТК, для любой цепи определяется равенством 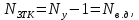 где 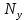 – число узлов цепи; – число узлов цепи; 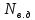 – число ветвей дерева в графе цепи. – число ветвей дерева в графе цепи.Составим уравнения по ЗТК для узлов рассматриваемой цепи: 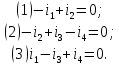 Нетрудно видеть, что любые два уравнения здесь линейно независимы, а третье – нет, его можно получить из предыдущих. Определим число независимых уравнений по ЗНК: 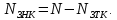 Утверждение 2 (принимаем без доказательства). Максимальное число независимых уравнений, которые можно составить по ЗНК, для любой цепи определяется равенством 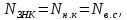 где 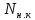 – число независимых контуров; – число независимых контуров; 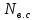 – число ветвей связи в графе цепи. – число ветвей связи в графе цепи.Примечание. Независимые контуры – контуры, дающие линейно независимые уравнения по ЗНК. Их число (за исключением частного случая одноконтурной схемы) всегда меньше общего числа контуров цепи. В планарной цепи независимыми контурами являются ее ячейки. Запишем уравнения для ячеек рассматриваемой цепи: 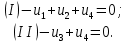 Уравнения линейно независимы. Добавление же уравнения для контура (III) приводит к линейной зависимости, так как это уравнение можно получить, сложив первые два: 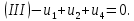 Но, с другой стороны, уравнения (I) и (III) или (II) и (III) также линейно независимы, поэтому выбирать в качестве независимых контуров только ячейки необязательно. Для непланарных же цепей такой подход вообще непригоден. В общем случае действуют так: строят граф цепи, выделяют дерево, и, присоединяя по очереди ветви связи, получают независимые контуры. Объединим независимые уравнения (например, 1, 2, I и II) в систему и исключим лишние переменные. Выразим, например, напряжения R-элементов через токи: 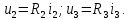 Соответственно, ток УИ: 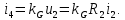 Система уравнений Кирхгофа сформирована: 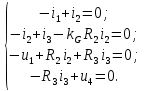 Наличие в цепи последовательных и параллельных соединений позволяет понизить порядок системы: из нее исключают уравнения для простейших узлов и ячеек. В данном примере: для узла (1) 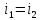 ; для ячейки (II) ; для ячейки (II) 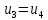 . Сохраним, например, переменные . Сохраним, например, переменные 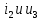 . Ток . Ток 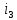 нужно тогда выразить через напряжение нужно тогда выразить через напряжение 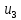 : :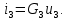 В итоге получим сокращенную систему уравнений Кирхгофа: 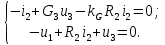 1.11. Свойства и теоремы электрических цепей 1.11.1. Свойства линейных стационарных цепей Рассмотрим линейную стационарную цепь Ц, состоящую из RLC-элементов и УИ (см. рис. 1.39). В момент времени 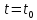 на вход цепи подается единственное воздействие, которое условно обозначим на вход цепи подается единственное воздействие, которое условно обозначим 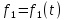 . Реакцию цепи обозначим . Реакцию цепи обозначим 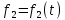 . Начальные запасы энергии в цепи отсутствуют. . Начальные запасы энергии в цепи отсутствуют. Рис. 1.39 При данных условиях справедливы следующие два свойства. Свойство однородности (принцип пропорциональности). Если величину воздействия изменить в K раз, величина реакции соответственно изменится в K раз. То есть, если новое воздействие 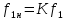 , ,то новая реакция 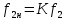 . .Свойство стационарности (принцип дифференцируемости). Если какое-либо новое воздействие численно является производной или интегралом от предыдущего, то и новая реакция может быть найдена как производная или интеграл от предыдущей. То есть, если 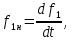 то 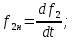 если 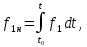 то 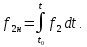 Если на цепь подается не одно, а n воздействий (см. рис. 1.40), то имеет место свойство аддитивности (принцип суперпозиции).  Рис. 1.40 Реакция цепи находится как сумма реакций на каждое воздействие в отдельности: 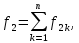 где 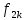 – реакция цепи на k-е воздействие – реакция цепи на k-е воздействие 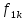 при равенстве нулю всех остальных воздействий. при равенстве нулю всех остальных воздействий.С учетом третьего свойства можно обобщить предыдущие два. Первое, например, будет звучать так: если величины всех воздействий одинаковым образом изменить в K раз, величина реакции соответственно изменится в K раз. 1.11.2. Теорема замещения Любую ветвь цепи с определенным напряжением 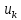 или током или током 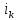 можно заменить соответственно на ИН или ИТ; режим работы цепи при этом не изменится (см. рис. 1.41). Теорему принимаем без доказательства. можно заменить соответственно на ИН или ИТ; режим работы цепи при этом не изменится (см. рис. 1.41). Теорему принимаем без доказательства. Рис. 1.41 1.11.3. Теорема взаимности (обратимости) Рассмотрим линейную пассивную цепь с одним источником. Если единственный в цепи ИН 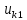 , действующий в ветви k, вызывает в ветви m ток , действующий в ветви k, вызывает в ветви m ток 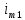 , то, будучи перенесенным в ветвь m, этот источник вызовет в ветви k ток , то, будучи перенесенным в ветвь m, этот источник вызовет в ветви k ток 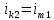 . Цифры 1 и 2 обозначают схемы цепи до и после переноса источника (см. рис. 1.42). Теорему принимаем без доказательства. . Цифры 1 и 2 обозначают схемы цепи до и после переноса источника (см. рис. 1.42). Теорему принимаем без доказательства.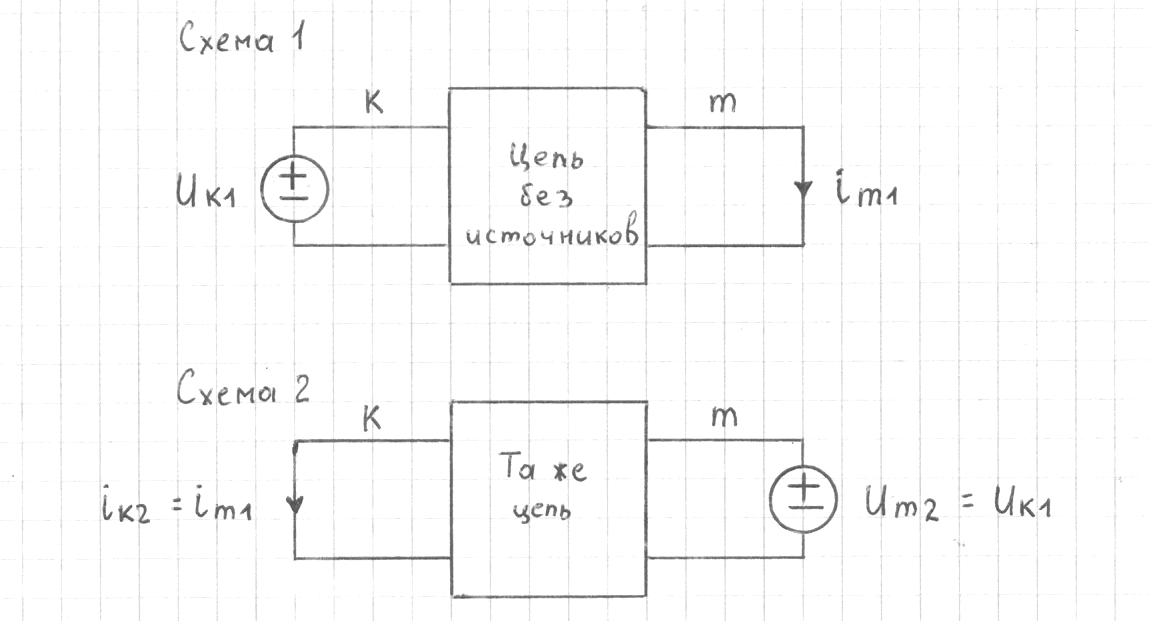 Рис. 1.42 Примечания. 1. Для цепи с ИТ формулировка теоремы дуальна. 2. К нелинейным и активным цепям теорема, как правило, неприменима. 1.11.4. Теоремы об эквивалентных источниках напряжения и тока (ТЭИН, ТЭИТ) Рассмотрим линейную пассивную резистивную цепь произвольного вида. Выделим в ней любую ветвь k (см. рис. 1.43). 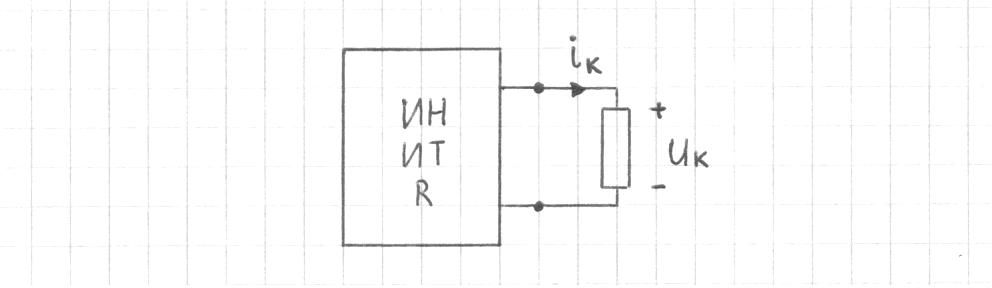 Рис. 1.43 Относительно выбранной ветви возможна эквивалентная замена всей остальной цепи по одному из вариантов, показанных на рис. 1.44. Вариант замены с источником напряжения обосновывается ТЭИН, вариант замены с источником тока – ТЭИТ. 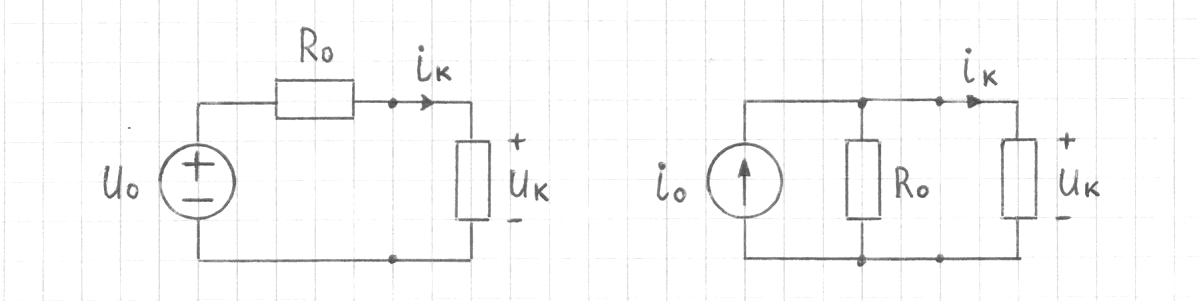 Рис. 1.44 Величины 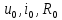 определяют по схемам, приведенным на рис. 1.45. определяют по схемам, приведенным на рис. 1.45.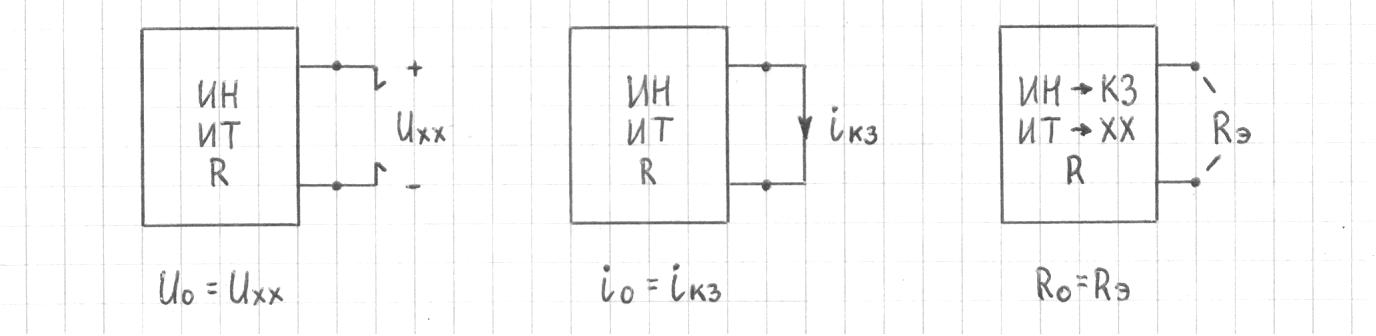 Рис. 1.45 Теорему принимаем без доказательства. Примечание. К нелинейным и активным цепям теорема применима ограниченно. 1.12. Режимы работы динамических цепей. Понятие о коммутации в цепи Цепь, в которой действует хотя бы один индуктивный или емкостный элемент, называется динамической. На различных этапах работы динамическая цепь может находиться в установившемся или неустановившемся режиме. В свою очередь, установившиеся режимы подразделяются на статический, периодический, почти периодический и хаотический, а неустановившиеся – на переходный и расходящийся. Установившийся режим – режим работы цепи при 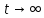 с ограниченными по уровню реакциями. Если все токи и напряжения в цепи постоянны, режим называют статическим, если изменяются по периодическим законам – – периодическим. с ограниченными по уровню реакциями. Если все токи и напряжения в цепи постоянны, режим называют статическим, если изменяются по периодическим законам – – периодическим.Переходный режим – режим работы цепи между двумя установившимися. Он возникает при подаче на цепь или снятии с цепи воздействия, при изменении формы или уровня воздействия, а также при изменении внутренних свойств цепи. Процессы в цепи при этом называют переходными, а причину, их вызвавшую – коммутацией. Строго говоря, коммутация – это изменение в цепи, выполняемое с помощью идеального ключа (см. рис. 1.46). Но если речь идет о динамической цепи, то коммутацией называют вообще любое изменение в цепи, вызывающее переходный процесс.  Рис. 1.46 При расчетах обычно полагают, что коммутация происходит в момент 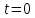 , а при , а при 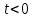 цепь находилась в установившемся режиме. Нахождение реакции цепи при цепь находилась в установившемся режиме. Нахождение реакции цепи при 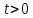 , то есть после коммутации, является основной задачей анализа цепи в переходном режиме. , то есть после коммутации, является основной задачей анализа цепи в переходном режиме. |
