СРС 1. Основные уравнения пространственной несущей системы со связями сдвига
 Скачать 148.52 Kb. Скачать 148.52 Kb.
|
|
Министерство Образования Республики Казахстан Международная Образовательная Корпорация Казахская Головная Архитектурно-Строительная Академия Факультет Общего Строительства СРС №1 По дисциплине: Проектирование и расчет высотных зданий Тема : «Основные уравнения пространственной несущей системы со связями сдвига» Выполнила: ст.гр. СТР (РПЗС) 15-5 Глызно Евгения Проверил: ассоц.проф. Келемешев А.Д. Алматы 2018 Основные уравнения пространственной несущей системы со связями сдвига Несущая система м/этажного здания м.б. представлена различными расчетными моделями: дискретными, континуальными и дискретно-континуальными. Дискретные модели сохраняют дискретное расположение связей и вертикальных элементов, заданное в действительной НС. Дискретизация сплошных элементов может углубляться путем их членения на более мелкие участки (применяется МКЭ) или путем замены континуума стержневой решеткой. Континуальные моделирассматривают здание как сплошную многоступенчатую призматическую оболочку с вертикальной осью (рис. 8,а) или как горизонтальную призматическую оболочку, опирающуюся на жесткие торцевые диафрагмы (рис. 8, б).  Рис. 8. Континуальные модели несущей системы здания: а – консольная призматическая оболочка с вертикальной осью; б – призматическая оболочка с горизонтальной осью; 1 – торцевые диафрагмы; 2 – поперечные несущие стены В первом случае при обеспечении жесткой монолитной связи продольных и поперечных стен и наличии жестких диафрагм – перекрытий модель позволяет считать многосвязный контур оболочки недеформируемым. Такой вариант модели уместен при расчете ядер-стволов. Вторая схема в отличие от первой предполагает перекрытия податливыми в их плоскости, а торцевые диафрагмы жесткими. В высоких панельных зданиях наружные стены выполняют, как правило, навесными. В этом случае требуется учет податливости связей и ослабление стен проемами, что достаточно сложно. Поэтому континуальные модели в расчетах таких зданий находят ограниченное применение. Дискретно-континуальные модели сохраняют заданное дискретное расположение вертикальных элементов НС, но заменяют сосредоточенные связи континуальными, т.е. непрерывно распределенными по высоте здания. Такая модель позволяет заменить, например, в односвязной конструкции (рис. 9) большое число неизвестных сил или перемещений одной функцией распределения искомого неизвестного по высоте здания. Математически это выражается заменой системы алгебраических уравнений высшего порядка одним дифференциальным уравнением. 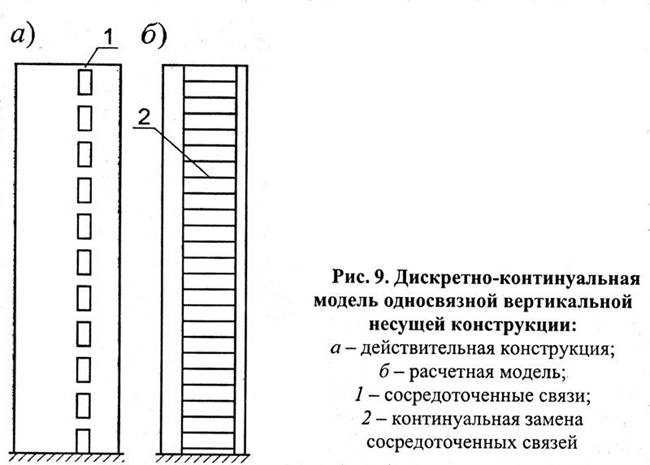 Переход к непрерывному распределению связей предполагает, что число этажей достаточно велико для того, чтобы сосредоточенные воздействия от перекрытий, перемычек или других связей сдвига можно было бы считать непрерывно распределенными по высоте несущей конструкции. Опыт проектирования показывает, что уже для 10-этажного здания такое предположение оправдывается. Дискретно-континуальные модели (ДКМ) более универсальны и удобны для расчета сложных НС м/этажных зданий, чем другие. Для сложной пространственной НС м/этажного здания Д.К.М представляет собой (рис. 10) пучок консольных тонкостенных стержней (поз. 1) прямоугольного профиля, соединенных в горизонтальных плоскостях перекрытиями (поз. 2), а по вертикальным швам – связями сдвига (поз. 3). 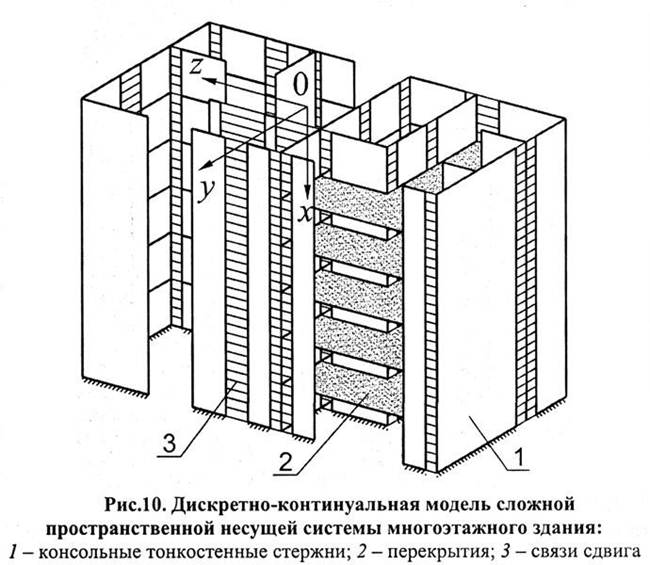 Заделка стержней (вертикальных элементов НС) в основании м.б. жесткой или упруго-податливой. На рис. 10 для удобства изображения перекрытия показаны как отдельные диски, расположенные поэтажно. Однако в расчете они, как и связи сдвига, предполагаются непрерывно распределенными по высоте здания. Расчет крупнопанельных бескаркасных зданий на основе рассмотренных моделей производится с использованием вычислительных комплексов типа ЛИРА-Windows и др. 1. Аншин Л.З. Исследование работы вертикальных диафрагм жесткости с учетом жесткости перемычек. В кн.: Работа конструкций жилых зданий из крупноразмерных элементов. - М., 1971, с.102-107 (Труды/ ЦНИИЭП жилища Госгражданстроя, № 2). 2. Аншин Л.З., Паныпин Л.Л. Исследование работы железобетонных конструкций на моделях. Строительная механика и расчет сооружений, 1976, № 4, с.38-40. 3. Байков В.Н., Горбатов С.В., Димитров З.А. Построение зависимости между напряжениями и деформациями сжатого бетона по системе нормируемых показателей. Изв.высш.учебн.заведений. Строительство и архитектура, Новосибирск, 1977, № 6, с.15-18. 4. Берг О.Я. Физические основы теории прочности бетона и железобетона. М., Госстройиздат, 1961. - 95 с. 5. Березин И.С., Жидков Н.П. Методы вычислений. Том второй. М.: Гос.изд.физ.-мат. литературы, I960. - 620 с. 6. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. М.: Наука, 1980. - 976 с. 7. Бурштейн Б.Л., Максимов Л.С., Тябликов Ю.Е., Скотын-ский В.И. Развитие средств экспериментальных исследований сооружений. В кн.: Экспериментальные исследования инженерных сооружений. - М.: Наука, 1973, с. 18-26. 8. Валь Е.Г. Расчет несущих диафрагм многоэтажных зданий как составных стержней и как пластин с проемами. В кн.: Конструкции крупнопанельных жилых домов. - М.: Стройиздат, 1976, с.75-83 (Труды/ЦНИИЭП жилища Госгражданстроя, вып.1). |
