Мухамедашим Н. 1-СРС. Основные уравнения пространственной несущей системы со связями сдвига (дискретноконтинуальная модель)
 Скачать 373.56 Kb. Скачать 373.56 Kb.
|
|
Министерство образования и науки Республики Казахстан Международная образовательная корпорация Казахская головная архитектурно-строительная академия  СРС-1 На тему: Основные уравнения пространственной несущей системы со связями сдвига (дискретно-конти-нуальная модель). Выполнил: ст. гр. Стр 17-11** Мухамедашим Н. А. Проверил(а):Келемешев А. Ж. Алматы 2020 Содержание
Расчетные модели диафрагмовых систем. Типы связей. Гипотезы, принимаемые при расчете Вертикальные несущие конструкции пространственной системы состоят из столбов диафрагм и ядер жесткости, колонн каркаса и связей, соединяющих эти элементы по вертикальным швам. Такими связями являются сварные соединения закладных деталей или выпусков арматуры, выступы плит перекрытия, перемычки или участки перекрытия над проёмами, бетонные шпонки. 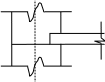 Рис. 1.1. Пример связей по вертикальным швам (выступ плиты перекрытия). Эти связи называются связями сдвига, так как они препятствуют свободному сдвигу соединяемых элементов по вертикальным швам при изгибе. Условно эти связи сдвига разделены на 3 типа: 1. Абсолютно жесткие; 2. Шарнирные; 3. Податливые. При деформировании вертикальных элементов, соединенных жесткими связями столбы диафрагм воспринимают внешний момент совместно, а связи остаются недеформированными и направляются по радиусу кривизны изогнутого элемента.                                    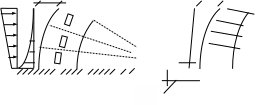 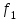 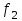 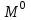 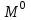  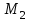   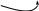 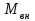 Рис. 1.2. Схемы деформирования вертикальных элементов при жёстких связях и при шарнирных связях соответственно В случае шарнирных связей сдвига столбы деформируются самостоятельно, а связи поворачиваются. В случае податливых связей сдвига внешние изгибающие моменты уравновешиваются внутренними изгибающими моментами в столбах 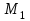 и и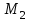 , и парой сил, возникающих за счет сопротивления связей сдвигу , и парой сил, возникающих за счет сопротивления связей сдвигу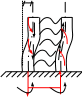   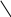 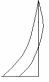 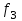 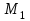 N b N b  N Nb M1+M2 N Nb M1+M2Рис. 1.3. Схема деформирования вертикальных элементов при податливых связях Для вариантов рассматриваем соединения, имеющие соотношения 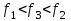 Вертикальные элементы в составе пространственной системы могут иметь 1 ряд связей сдвига или несколько. В этих случаях диафрагмы называются односвязными и многосвязными. Если диафрагма соединена с элементом рамы связями, то соединение называется рама-диафрагма.   односвязная двусвязная односвязная двусвязная двусвязная Рис. 1.4. Примеры видов диафрагм и рамо-диафрагм. Колонны каркаса имеют изгибы и жесткость значительно меньшую, чем столбы диафрагм, поэтому они не могут рассматриваться как самостоятельные элементы Т.е. в каркасных системах считается, что колонны воспринимают только продольные усилия и местные изгибающие моменты от деформирования связей. Диафрагмовые системы принято схематизировать континуальной, дискретной и дискретно-континуальной моделями. Дискретная модель сохраняет дискретное расположение элементов и связей сдвига. Причем элементы системы подвергаются более детальной дискретизации на конечных элементах в методе конечных элементов либо производится замена несущей системы стержневой решеткой в методе замены континуума стержневой решеткой. Дискретная модель может применяться для расчета простых систем или отдельных диафрагм. Континуальная модель представляет собой пространственную несущую систему в виде сплошной многостенчатой призматической оболочки с вертикальными или горизонтальными осями.   Рис. 1.5. Континуальная модель диафрагмовой системы. В многоэтажных зданиях наружные стены преимущественно выполняют ограждающие функции, поэтому континуальные модели для таких систем неприменимы. Они используются для расчета ядер жесткости. Дискретно-континуальная модель сохраняет дискретное расположение вертикальных несущих элементов, а дискретные связи сдвига заменяют непрерывным их распределением по высоте несущей системы.  Рис. 1.6. Дискретно континуальная модель диафрагмовой системы. В результате такой замены, при расчете больших систем алгебраических уравнений с большим количеством неизвестных заменяется одним диференциальным уравнением или системой диференциальных уравнений, порядок которых равен числу вертикальных швов между несущими вертикальными элементами. Разновидностью дискретно-континуальных моделей являются консольная и консольно-заменяющая модель. В консольной модели связи сдвига считаются либо шарнирными, либо абсолютно жесткими. Такая модель используется для расчета связевых каркасов, а при небольшой модификации и для расчета бескаркасных систем.  Рис. 1.7. Консольно заменяющая модель диафрагмовой системы В консольно-заменяющих моделях несущая система заменяется одним консольным стержнем, изгибная и сдвиговая жесткость которого эквивалентна аналогичным характеристикам всей системы. Расчет по общей дискретно-континуальной модели достаточно сложен, поэтому в ней используются возможные упрощения. В частности симметричные в плане несущие системы разбиваются на 2 независимые плоскопараллельные поперечные и продольные несущие системы. Кроме того, во всех моделях для удобства расчета начало вертикальной координаты несущей системы располагают в верхней точке здания, а ось направляют вниз. Помимо моделей схематизации при расчете пространственных систем принимают следующие рабочие гипотезы: 1) плоские стенки диафрагм жесткости не испытывают сопротивления чистого кручения; 2) междуэтажные перекрытия считаются абсолютно жесткими в своей горизонтальной плоскости и абсолютно гибкими из неё; 3) в связях пренебрегают осевыми деформациями; 4) материал элементов несущей системы считается физически линейным; 5) считается, что при деформировании несущей системы её элементы получают малые перемещения. Предварительный расчет количества диафрагм жесткости Подбор необходимого количества диафрагм жесткости производится в 2-х взаимно-ортогональных направлениях. Этот выбор возможен только для несущих систем, близких к симметричным в плане, которые включают в себя диафрагмы близкие по изгибной и осевой жесткости, воспринимающие близкие по значению вертикальные нагрузки. Если несущая система обладает ярко выраженной асимметрией, или в системе используются диафрагмы различной жесткости, то предварительный выбор количества диафрагм по сравнению с уточнённым расчетом вносит погрешность  30%. 30%.В общем случае количество диафрагм, располагаемых параллельно одной из осей плана здания, ориентировочно задаётся из условия 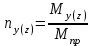 , ,где 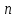 – количество диафрагм параллельных оси y(z). – количество диафрагм параллельных оси y(z). z y Рис. 1.8 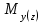 – равнодействующий изгибающий момент от действия вертикальных и горизонтальных нагрузок, приложенных по всей несущей системе, и действующих в плоскости – равнодействующий изгибающий момент от действия вертикальных и горизонтальных нагрузок, приложенных по всей несущей системе, и действующих в плоскости 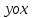 и и 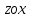 . . 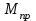 – предельный допустимый момент, воспринимаемый одной диафрагмой жесткости. – предельный допустимый момент, воспринимаемый одной диафрагмой жесткости.Суммарный изгибающий момент, действующий на всю несущую систему, от внешних нагрузок в плоскости 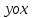 или или 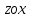 устанавливается исходя из опыта проектирования по приближенной формуле устанавливается исходя из опыта проектирования по приближенной формуле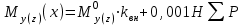 , (1) , (1)где 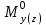 – консольный изгибающий момент, действующий на всю несущую систему в соответствующей плоскости от горизонтальной нагрузки – консольный изгибающий момент, действующий на всю несущую систему в соответствующей плоскости от горизонтальной нагрузки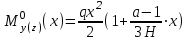 , (2) , (2)где 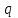 – интенсивность ветровой нагрузки в уровне верха здания; – интенсивность ветровой нагрузки в уровне верха здания; 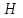 – полная высота здания; – полная высота здания; 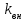 – коэффициент, учитывающий внецентренное приложение вертикальной нагрузки. – коэффициент, учитывающий внецентренное приложение вертикальной нагрузки.На первом этапе, когда неизвестны эксцентриситеты вертикальной нагрузки 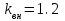 . .Если же расположение диафрагм известно, и известны эксцентриситеты приложения вертикальной нагрузки, то вместо 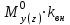 следует принимать фактический момент от вертикальных и горизонтальных нагрузок, действующих на всю систему; следует принимать фактический момент от вертикальных и горизонтальных нагрузок, действующих на всю систему; 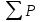 – суммарная нагрузка с учетом веса конструкции и временных нагрузок, собранная со всех этажей в пределах плана здания. – суммарная нагрузка с учетом веса конструкции и временных нагрузок, собранная со всех этажей в пределах плана здания.Предельно допустимый момент, действующий в одной диафрагме, определяется из условия ограничения горизонтального перемещения верха диафрагмы и назначается из условия 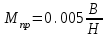 , (3) , (3)где 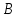 – изгибная жесткость диафрагмы с учетом податливости связей сдвига (в направлении большей жесткости); – изгибная жесткость диафрагмы с учетом податливости связей сдвига (в направлении большей жесткости); 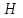 – полная высота здания. – полная высота здания. Рис. 1.9 В условии (1) второе слагаемое обобщенным образом учитывает увеличение прогиба диафрагм за счет явления продольного изгиба от вертикальных нагрузок. В условии (3) эмпирическим способом учтен осредненный коэффициент надежности по нагрузке 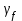 . .После предварительного определения количества диафрагм в 2-х перпендикулярных плоскостях выполняют их расстановку в плане по соответствующим правилам и собирают фактическую нагрузку на них. После расстановки диафрагм и определения, действующих в них фактических вертикальных нагрузок количество диафрагм необходимо уточнить, с тем, чтобы обеспечить их прочность на срез по горизонтальному шву. Дополнительной проверки прочности на срез не требуется, если 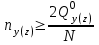 , (4) , (4)где 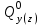 – поперечная сила в расчетном сечении диафрагмы от горизонтальных нагрузок – поперечная сила в расчетном сечении диафрагмы от горизонтальных нагрузок 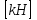 ; ; 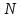 – продольная вертикальная сила в одной диафрагме: – продольная вертикальная сила в одной диафрагме: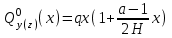 . .Список используемой литературы ОБЕСПЕЧЕНИЕ ТРЕБУЕМОГО УРОВНЯ НАДЕЖНОСТИ ЗДАНИЙ И СООРУЖЕНИЙ, В. Н. Левченко, Д. В. Левченко, В. Ф. Кириченко. А. В. Заруба, Е. И. Кельман ЖЕЛЕЗОБЕТОННЫЕ КОНСТРУКЦИИ. СПЕЦИАЛЬНЫЙ КУРС, В. Н. Байков, Э. Е. Сигалов https://uchebana5.ru/cont/2791533.html http://dpvolga.ru/uroven-otvetstvennosti-zdaniya/ |
