Теплотехника Селявсинов бгб-19. Селявсинов БГБ-19 Теплотехника. Основные условные обозначения
 Скачать 247.6 Kb. Скачать 247.6 Kb.
|
|
P2= P1=300 000 Па, Температура в конце процесса, К Т2= Т1∙ ε=290*1,2=348 Средняя температура, К Тср=(Т1+Т2)/2= 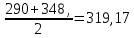 Или в градусах Цельсия tср= Тср – 273,15=319,17-273,15=46,015 Средние массовые теплоемкости компонентов при постоянном давлении Срсрi при средней температуре определяются для каждого из пяти газов. Для углеводородных газов (метан, этан, пропан и т.д.) по графикам из пособия (рисунки 1.14 – 1.19) по температуре в градусах Кельвина.. Для неуглеводородных газов (воздух, азот, кислород и т.д.) рассчитывается по формулам из Приложения 1.1 практического пособия. Например, для воздуха по формуле вначале определяется мольная теплоемкость 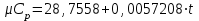 , ,где t = tср – средняя температура из предыдущего пункта, °С. Затем рассчитывается массовая теплоемкость воздуха делением мольной теплоемкости воздуха на молярную массу воздуха 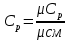 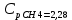 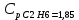 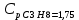 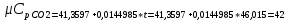 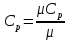 = =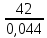 =0,954 =0,954 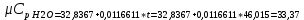 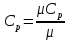 = =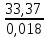 =1,853 =1,853 Средняя массовая теплоемкость газовой смеси при постоянном давлении, кДж/(кг∙°С) 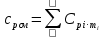 =2,116 =2,116где mi - массовые доли из п. 1.5. Средняя массовая теплоемкость газовой смеси при постоянном объеме, кДж/(кг∙°С) 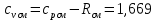 Показатель адиабаты k 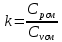 =1,268 =1,268Термодинамическая работа процесса , кДж/кг l= P1 ∙ (V2-V1)=25,94 Изменение внутренней энергии, кДж/кг Δu = Cv см ∙(T2-Т1)=96,84 Изменение энтальпии, кДж/кг Δh = Cp см ∙(T2-Т1)=122,78 Средняя массовая политропная теплоемкость процесса, кДж/(кг∙°С) 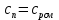 =2,116 =2,116Теплота процесса, кДж/кг q = Δh=122,78 Изменение удельной энтропии процесса, кДж/(кг ∙°С) 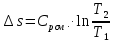 =0,3858 =0,3858Расчет политропного процесса с n2 Показатель политропы n= n2=0,4 Давление в конце процесса, Па 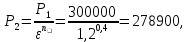 Температура в конце процесса, К Т2= Т1/ ε(n-1)= 323,69 Средняя температура, К Тср=(Т1+Т2)/2=306,92 Или в градусах Цельсия tср= Тср – 273,15=33,77 Средние массовые теплоемкости компонентов при постоянном давлении Срсрi при новой средней температуре определяются для каждого из пяти газов. 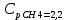 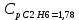 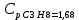 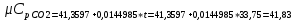 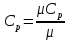 = =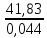 =0,95 =0,95 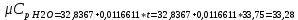 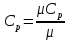 = =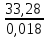 =1,846 =1,846 Средняя массовая теплоемкость газовой смеси при постоянном давлении, кДж/(кг∙°С) 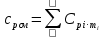 =2,043 =2,043где mi - массовые доли из п. 1.5. Средняя массовая теплоемкость газовой смеси при постоянном объеме, кДж/(кг∙°С) 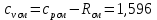 Показатель адиабаты k 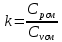 =1,280 =1,280Термодинамическая работа процесса , кДж/кг 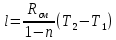 =25 =25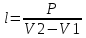 =24,12 =24,12Изменение внутренней энергии, кДж/кг Δu = Cv см ∙(T2-Т1)=53,52 Изменение энтальпии, кДж/кг Δh = Cp см ∙(T2-Т1)=68,52 Средняя массовая политропная теплоемкость процесса, кДж/(кг∙°С) 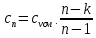 =2,341 =2,341Теплота процесса, кДж/кг q = cn ∙ (T2 – T1)=78,52 Изменение удельной энтропии процесса, кДж/(кг ∙°С) 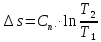 =0,2561 =0,2561Расчет политропного процесса с n3=1 Показатель политропы n=1, процесс изотермический; Давление в конце процесса, Па 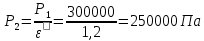 , ,Температура в конце процесса, К Т2= Т1=290 К Средняя температура, К Тср=(Т1+Т2)/2= 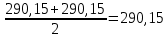 Или в градусах Цельсия tср= Тср – 273,15=290,15-273,15=17 2.3.5 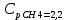 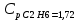 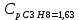 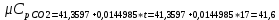 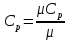 = =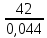 =0,945 =0,945 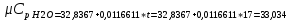 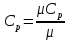 = =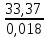 =1,834 =1,834 Средняя массовая теплоемкость газовой смеси при постоянном давлении, кДж/(кг∙°С) 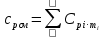 =2,028 =2,028где mi - массовые доли из п. 1.5. Средняя массовая теплоемкость газовой смеси при постоянном объеме, кДж/(кг∙°С) 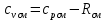 =1,58 =1,58Показатель адиабаты k 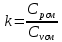 =1,2837 =1,2837Термодинамическая работа процесса , кДж/кг 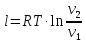 = lпот =23,687 = lпот =23,687Изменение внутренней энергии, кДж/кг Δu = 0 Изменение энтальпии, кДж/кг Δh = 0 Средняя массовая политропная теплоемкость процесса, кДж/(кг∙°С) равна бесконечности. Теплота процесса, кДж/кг q = l=23,687. Изменение удельной энтропии процесса, кДж/(кг ∙°С) 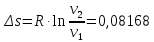 Расчет политропного процесса с n4 Показатель политропы n= n4=1,2 Давление в конце процесса, Па 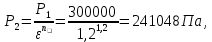 Температура в конце процесса, К Т2= Т1/ ε(n-1)= 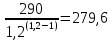 Средняя температура, К Тср=(Т1+Т2)/2= 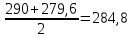 Или в градусах Цельсия tср= Тср – 273,15=284,8-273,15=11,65 Средние массовые теплоемкости компонентов при постоянном давлении Срсрi при новой средней температуре определяются для каждого из пяти газов. 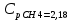 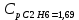 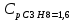 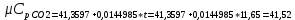 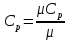 = =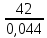 =0,943 =0,943 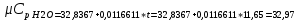 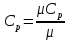 = =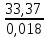 =1,831 =1,831 Средняя массовая теплоемкость газовой смеси при постоянном давлении, кДж/(кг∙°С) 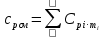 =2,0075 =2,0075где mi - массовые доли из п. 1.5. Средняя массовая теплоемкость газовой смеси при постоянном объеме, кДж/(кг∙°С) 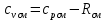 =1,5595 =1,5595Показатель адиабаты k 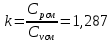 Термодинамическая работа процесса , кДж/кг 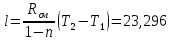 Изменение внутренней энергии, кДж/кг Δu = Cv см ∙(T2-Т1)=-16,218 Изменение энтальпии, кДж/кг Δh = Cp см ∙(T2-Т1)=-20,878 Средняя массовая политропная теплоемкость процесса, кДж/(кг∙°С) 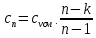 =-0,678 =-0,678Теплота процесса, кДж/кг q = cn ∙ (T2 – T1)=7,05 Изменение удельной энтропии процесса, кДж/(кг ∙°С) 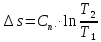 =0,0247 =0,0247Расчет политропного процесса с n5 Показатель политропы n=kзад=cp см/cv см,= 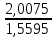 =1,287 =1,287где ср см – средняя изобарная теплоемкость газов из п.2.4; сv см – средняя изохорная теплоемкость газов из п.2.4; Давление в конце процесса, Па 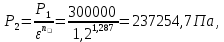 Температура в конце процесса, К Т2= Т1/ ε(n-1)= 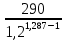 =275,2, =275,2,Средняя температура, К Тср=(Т1+Т2)/2= 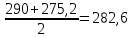 , ,Или в градусах Цельсия tср= Тср – 273,15=282,6-273,15= 9,457, Средние массовые теплоемкости компонентов при постоянном давлении Срсрi при новой средней температуре определяются для каждого из пяти газов. 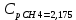 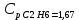 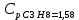 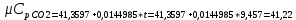 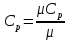 = =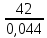 =0,936 =0,936 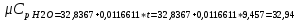 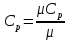 = =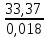 =1,830 =1,830 Средняя массовая теплоемкость газовой смеси при постоянном давлении, кДж/(кг∙°С) 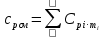 =1,9996 =1,9996где mi - массовые доли из п. 1.5. Средняя массовая теплоемкость газовой смеси при постоянном объеме, кДж/(кг∙°С) 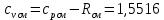 Уточняется показатель адиабаты kпол 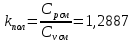 Если ǀкзад-кполǀ > 0,01, то прин.ем новое кзад=кпол и возвращаемся в пункт 2.5.2. Термодинамическая работа процесса , кДж/кг 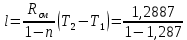 *(275,2-290)=23,1 *(275,2-290)=23,1Изменение внутренней энергии, кДж/кг Δu = Cv см ∙(T2-Т1)=1,5526*(275,2-290)=-22,97 Изменение энтальпии, кДж/кг Δh = Cp см ∙(T2-Т1)=1,9996*(275,2-290)=-29,59 Средняя массовая политропная теплоемкость процесса, кДж/(кг∙°С) с = 0 Теплота процесса, кДж/кг q = 0 Изменение удельной энтропии процесса, кДж/(кг ∙°С) 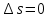 |
