Раева_Фролкова_Н_2013_end. Основные законы равновесия жидкость пар бинарных систем
 Скачать 1.12 Mb. Скачать 1.12 Mb.
|
2.2. Законы КоноваловаЗаконы Коновалова устанавливают связи между изменениями состава и давления (при T= const), состава и температуры (при Р = const) в бинарных двухфазных системах и лежат в основе теории процессов перегонки и ректификации бинарных смесей. Законы действуют при P = const или T = const. Первый закон Коновалова Закон справедлив для составов бинарной системы, в которых Преобразуем выражение (29) и проанализируем знаки величин, входящих в него: Поскольку если Температура кипения раствора возрастает (уменьшается) при увеличении концентрации в растворе того компонента, содержание которого в паре меньше (больше), чем в растворе. Насыщенный пар по сравнению с жидкостью обогащен тем компонентом, добавление которого в жидкую фазу снижает ее температуру кипения. Под добавлением компонента в жидкую фазу подразумевается бесконечно малое увеличение его концентрации. При постоянной температуре из (28) имеем: Здесь Давление пара раствора возрастает (уменьшается) при увеличении в растворе концентрации того компонента, содержание которого в паре больше (меньше), чем в растворе. Насыщенный пар по сравнению с жидкостью обогащён тем компонентом, добавление которого в жидкую фазу повышает давление в системе. Объединенная формулировка первого закона Коновалова для изобарических (изотермических) условий: пар по сравнению с жидкостью обогащен тем компонентом, добавление которого в жидкую фазу понижает ее температуру кипения (повышает давление над раствором). Графическая интерпретация закона для зеотропных смесей при Р=const представлена на рис. 10а. Пар состава 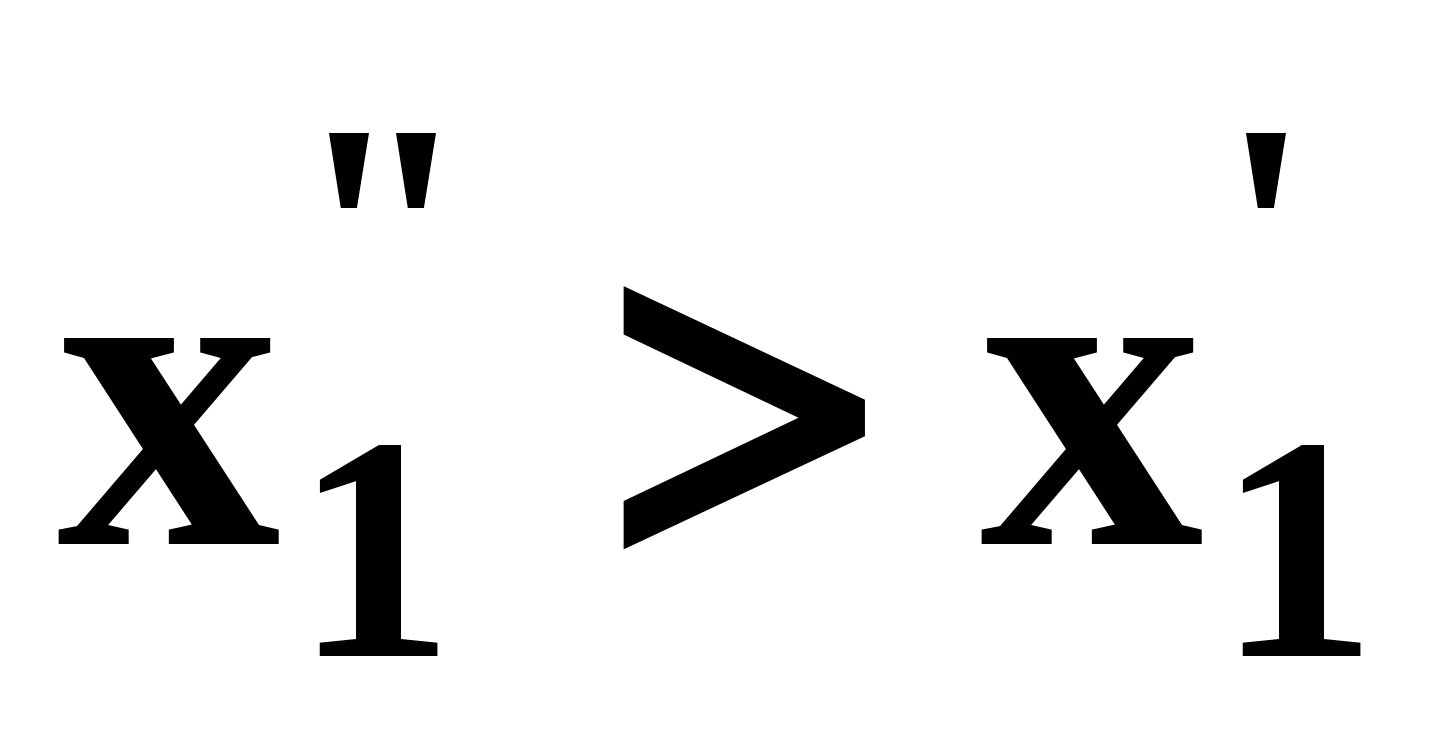 ) уменьшает температуру кипения вдоль изобары ( ) уменьшает температуру кипения вдоль изобары (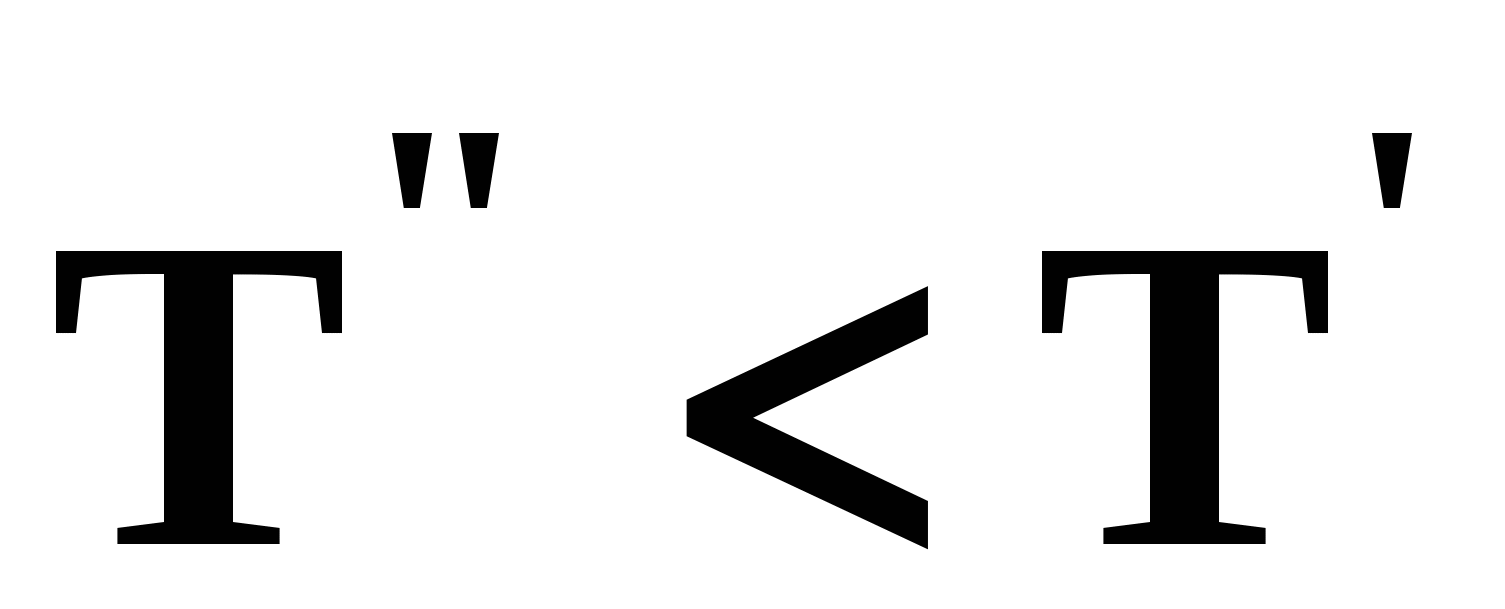 ). ).При Т=const (рис. 10б) пар обогащен компонентом 1 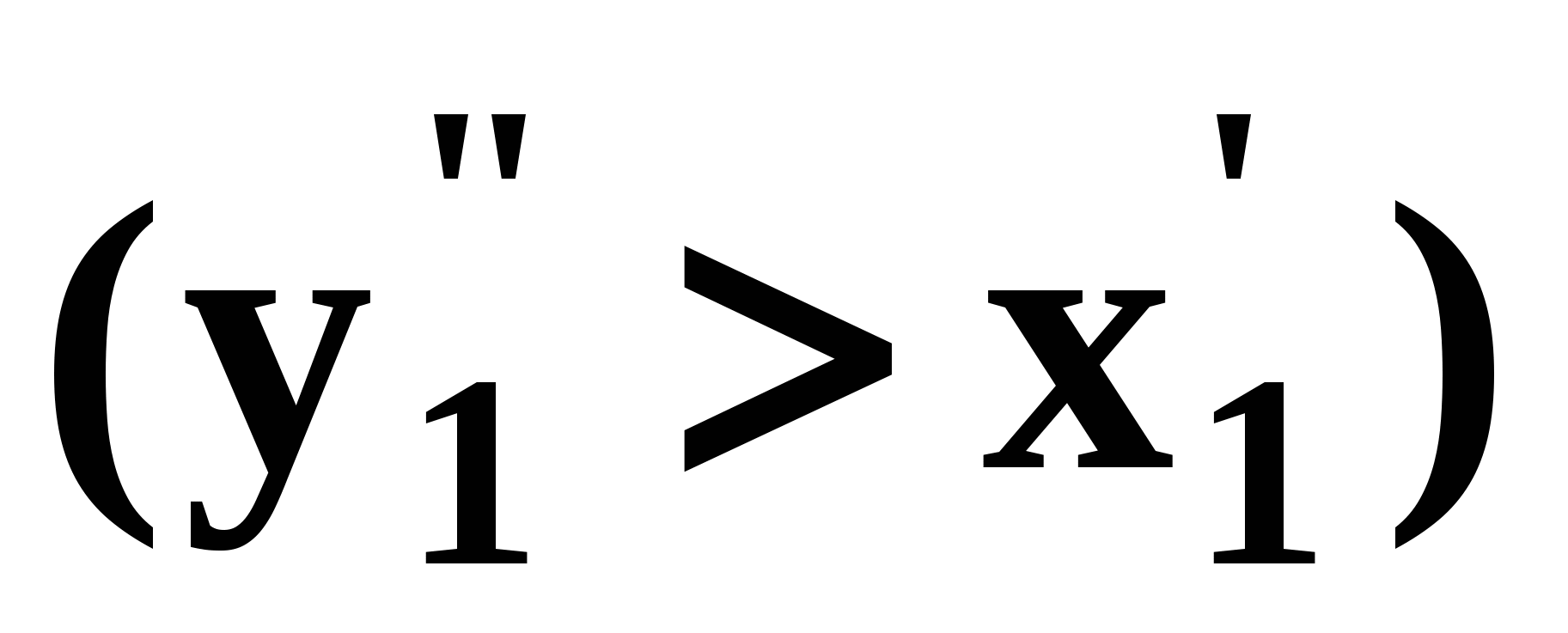 , добавление которого в жидкость ( , добавление которого в жидкость (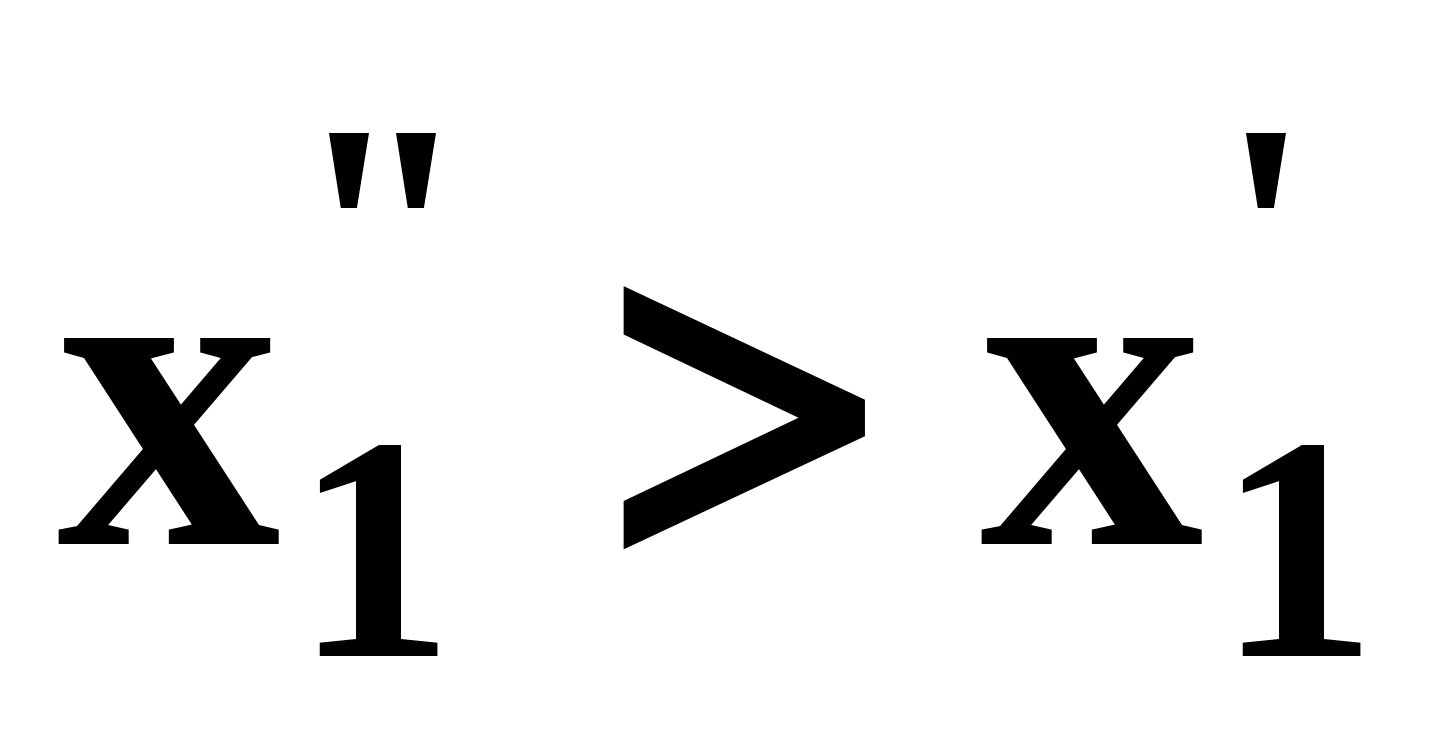 ) повышает давление в системе ( ) повышает давление в системе (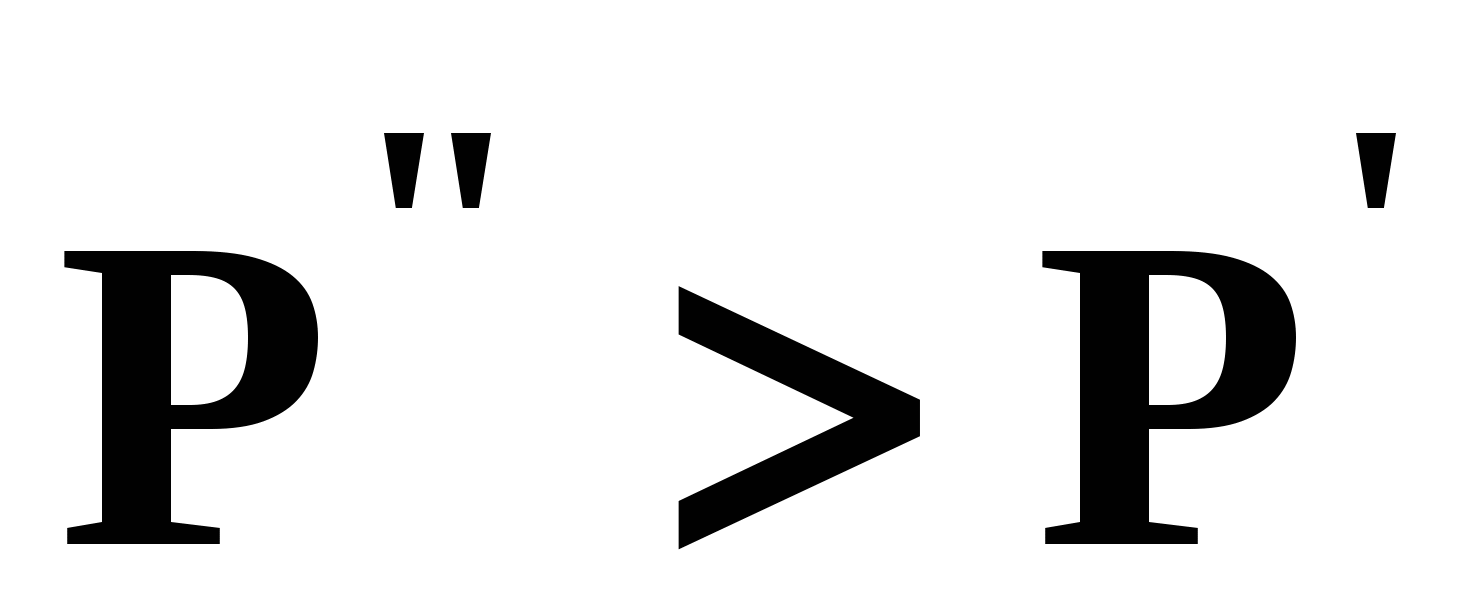 ). ).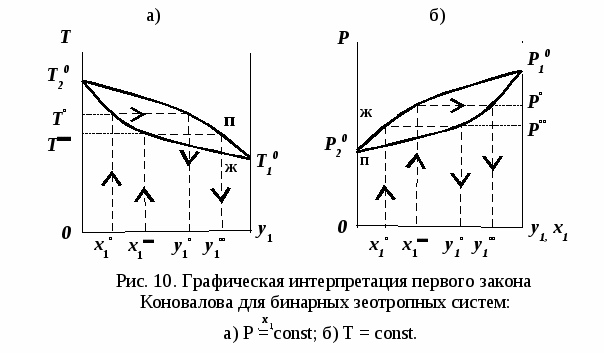 В таблице 1 приведены экспериментальные данные ПЖР, позволяющие проиллюстрировать закон Коновалова на примере системы с положительным азеотропом. Рассмотрим данные при 70 град. С (х1аз 90 мольн. %). Для области соcтавов жидкой фазы 0<x1<x1аз пар обогащен этанолом (y1 >x1), при добавлении которого к жидкой фазе общее давление над раствором растет. Для составов, расположенных «правее» азеотропа x1аз <x1< 1 пар обогащен водой (y2 > x2), при добавлении которой к жидкой фазе общее давление над раство- ром также увеличивается. Таким образом, в любой области составов пар по сравнению с жидкостью обогащен тем компонентом, добавление которого в жидкую фазу повышает давление над раствором. Таблица 1. Данные парожидкостного равновесия в системе этанол (1) –вода (2) [2].
Второй закон Коновалова Второй закон Коновалова справедлив для фаз любой природы: если температура и давление сосуществования двух бинарных фаз имеют экстремум (максимум или минимум), то составы фаз одинаковы. В случае систем жидкость – пар второй закон Коновалова относится к азеотропным точкам. Представим уравнения (31), (32) в виде: В точке азеотропа равны составы фаз: 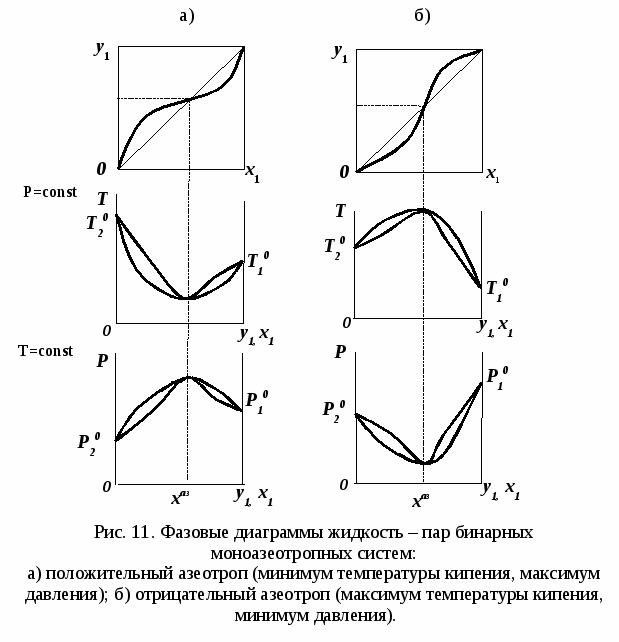 Приведем прямую и обратную формулировки закона: Если температура и давление сосуществования паровой и жидкой фаз имеют экстремум (максимум или минимум), то составы фаз одинаковы. Если бинарная смесь имеет точку, которая характеризуется равенством составов паровой и жидкой фаз, то на концентрационных зависимостях В точке азеотропа в силу равенства составов фаз коэффициенты распределения компонентов Точки азеотропов и чистых компонентов, в которых Коэффициенты активности компонентов в бесконечно разбавленном растворе Параметры бинарных азеотропов (состав, температура, давление) являются необходимой информацией при разработке принципиальных технологических схем разделения бинарных и многокомпонентных смесей. Вместе с данными ПЖР они публикуются в периодической физико-химической литературе, приводятся в справочниках [2-5], а также содержатся в специализированных банках данных [6]. Третий закон Коновалова Запишем частные формы уравнения Ван-дер-Ваальса для фазовых переходов жидкость пар (23) и пар жидкость (26) в изобарических условиях: После преобразования получим: 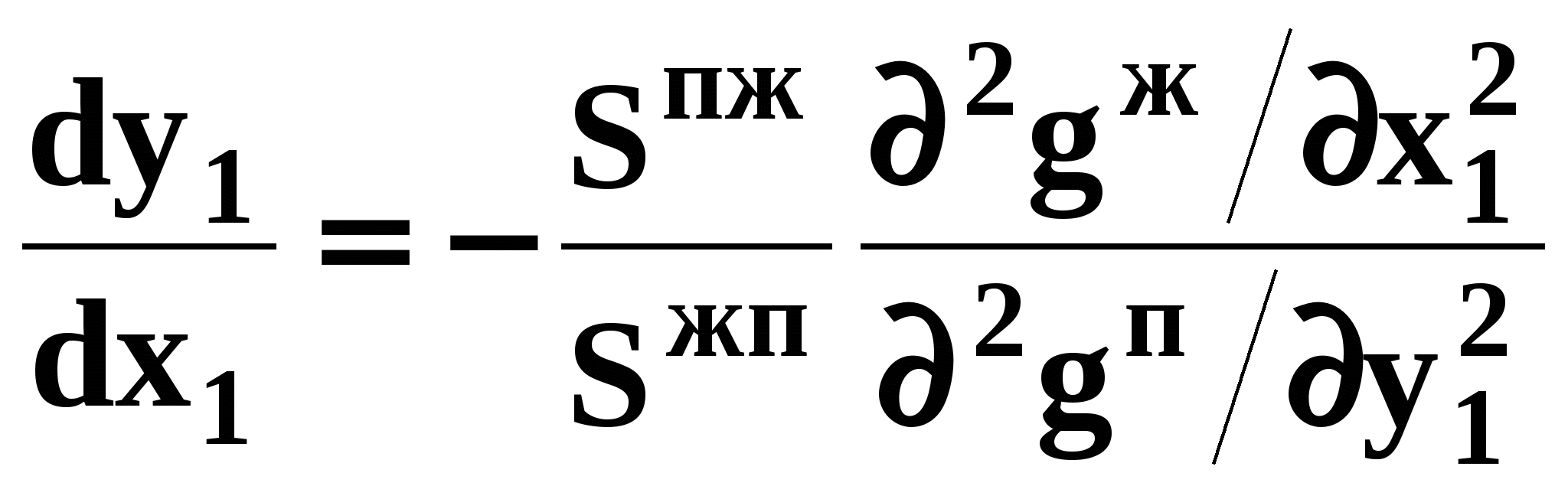 . (37) . (37)а) б) в) 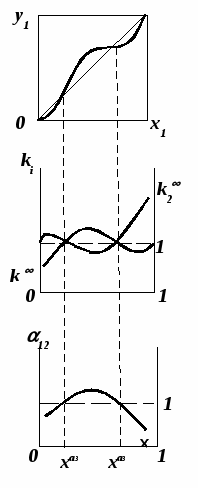 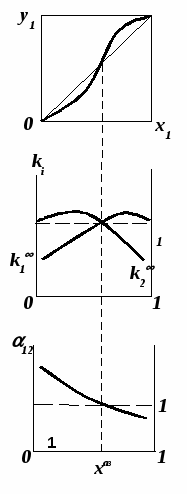 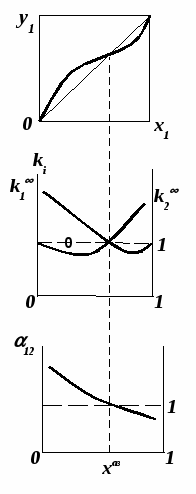 x1 Рис. 12. Зависимости коэффициентов распределения и относительных летучестей компонентов от состава в бинарных азеотропных системах: а) положительный азеотроп; б) отрицательный азеотроп; в) биазеотропная система. В силу устойчивости фаз вторые производные 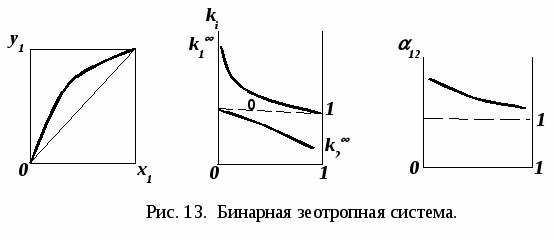 составы равновесных паровой и жидкой фаз в изотермических и изобарических условиях изменяются однонаправлено (симбатно). Положение о симбатности изменений составов пара и жидкости называют третьим законом Коновалова. На рисунке 14 дана графическая интерпретация закона. Независимо от типа системы при увеличении содержания первого компонента в жидкой фазе ( 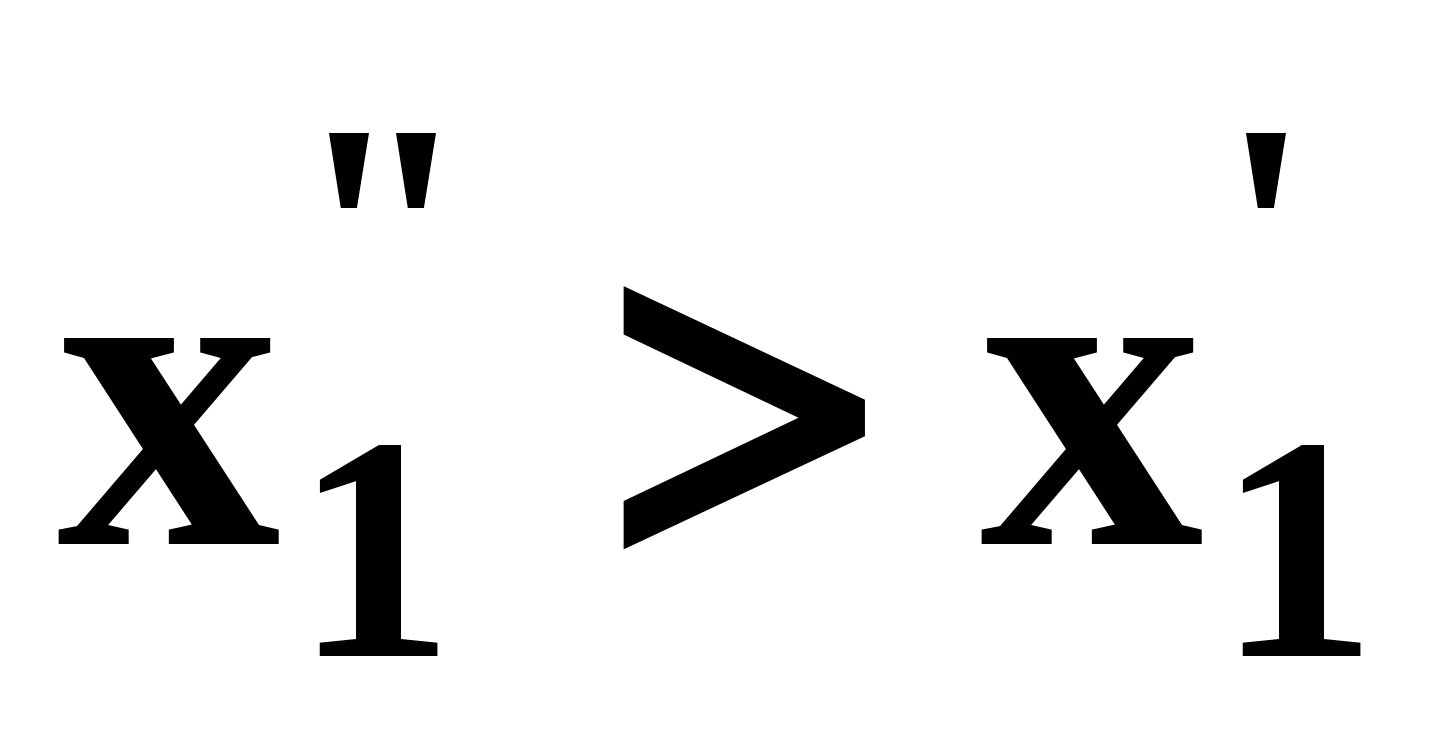 )увеличивается его концентрация в паре )увеличивается его концентрация в паре 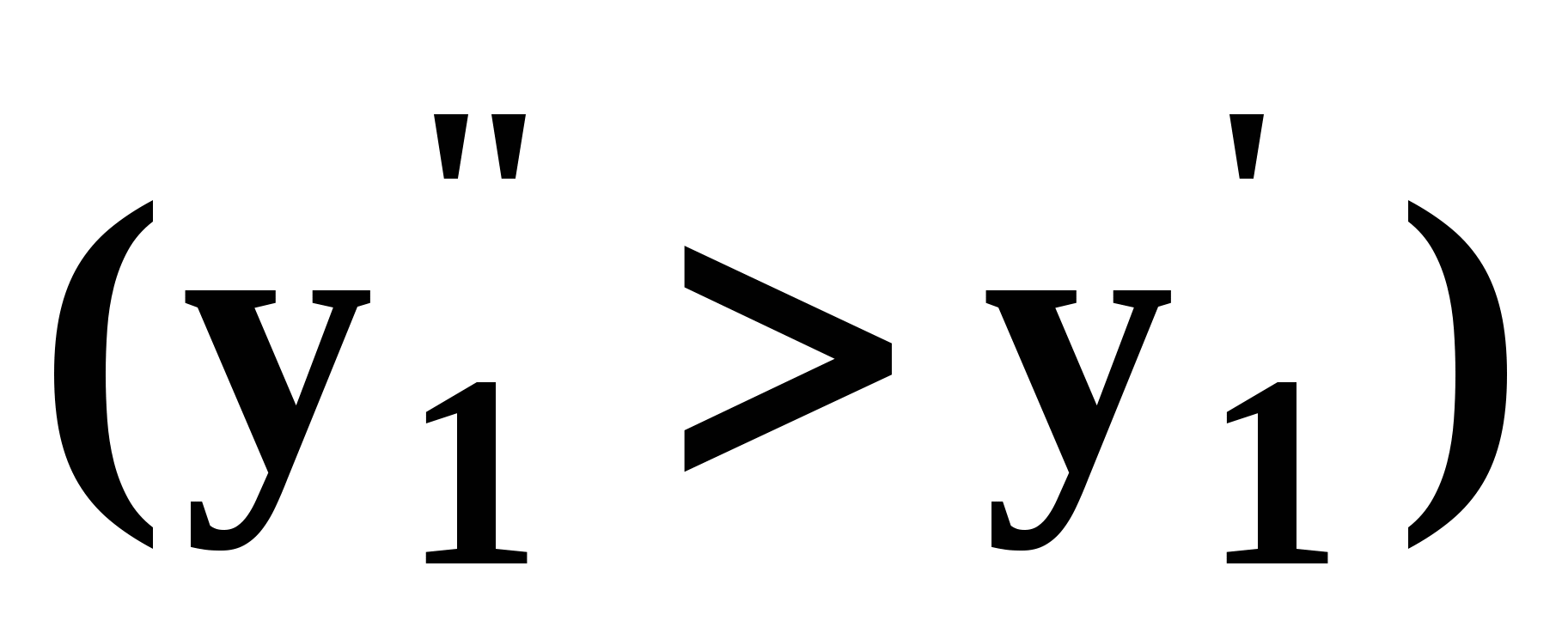 . .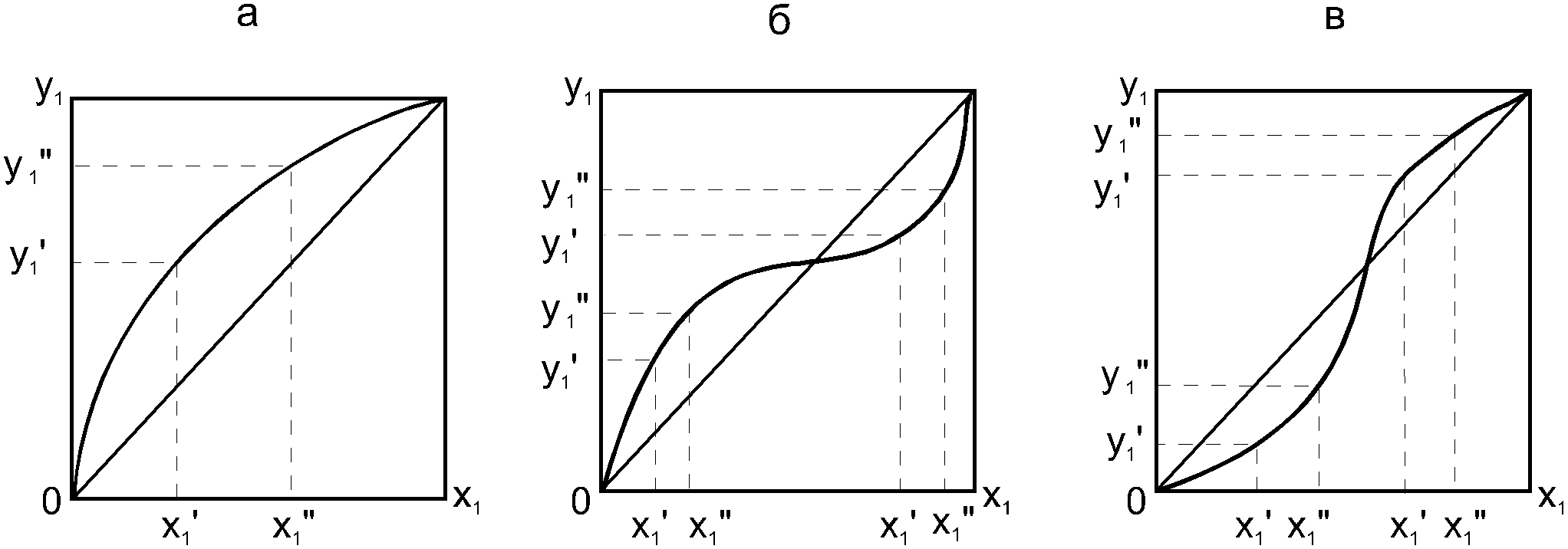 Рис. 14. Графическая интерпретация третьего закона Коновалова в системах с разным характером отклонения от идеального поведения: а) зеотропная система; б), в) азеотропные системы. В бинарных системах законы Коновалова справедливы для условий, удаленных от критических. 2.3. Законы Вревского Законы Вревского описывают поведение систем при варьировании внешних параметров (температура, давление) при закрепленном составе жидкой фазы. Для их математической интерпретации получим раскрытую форму условия фазового равновесия в виде: С учетом соотношений (20а), (21а) условие (38б) принимает вид: Раскроем полные дифференциалы разности химических потенциалов: 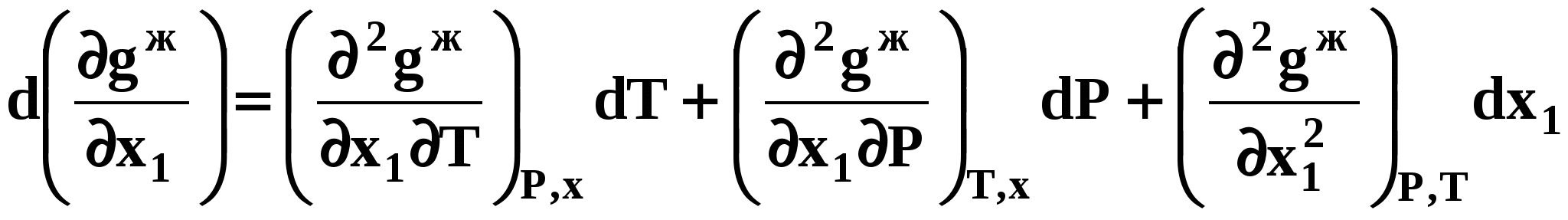 , (40а) , (40а)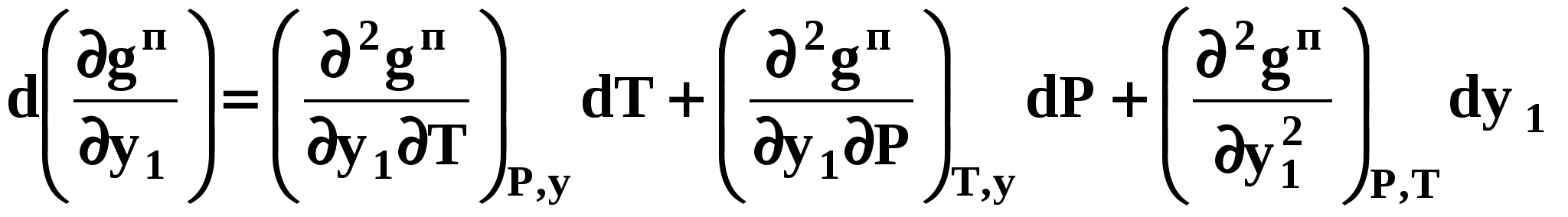 . (40б) . (40б)Величина второй производной не зависит от порядка дифференцирования (соотношения Максвелла). Тогда, если представить сомножители при переменных уравнений (39) в виде частных производных 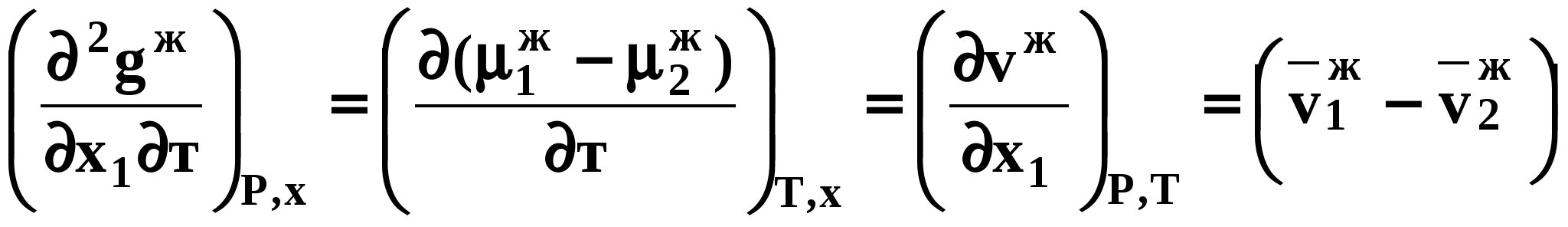 , (41) , (41)получим: 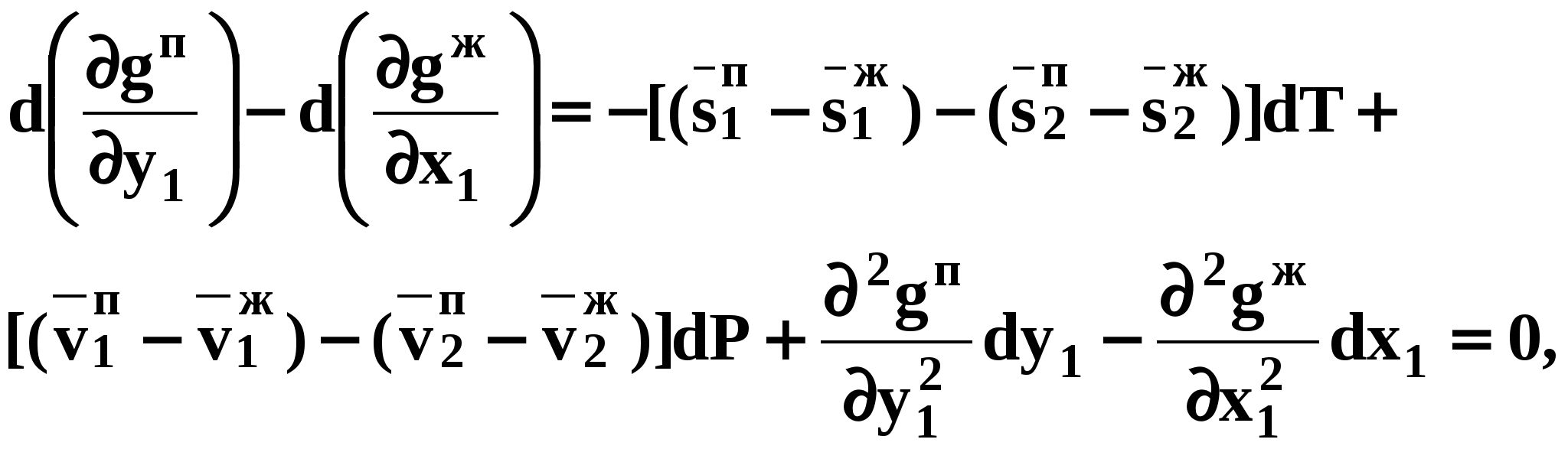 (42) (42)где верхней планкой обозначены парциальные величины. Последние были введены Льюисом для учета нелинейности зависимостей свойств бинарных смесей мы от состава. В окончательном виде раскрытая форма условия фазового равновесия выражается следующим образом: Здесь При допущении об идеальном поведении паровой фазы и в условиях, удаленных от критических, объемная составляющая в уравнении (43) обращается в нуль. Математический вывод законов Вревского базируется на анализе знаков всех величин, входящих в выражение (43).Их действие ограничено критическими точками фазового равновесия жидкость – пар. Первый закон Вревского Закон определяет характер влияния внешних параметров на содержание компонента в паровой фазе при закрепленном составе жидкой фазы. С учетом Для идеального пара ( При постоянном составе жидкой фазы и увеличении температуры пар всегда обогащается тем компонентом, парциальная молярная теплота парообразования которого больше. Парциальные молярные теплоты испарения определяются через теплоты испарения чистых веществ При отсутствии экспериментальных данных о теплотах смешения (избыточных энтальпиях) растворов парциальные молярные теплоты испарения Рисунок 15 иллюстрирует графическое определение парциальных величин. Значения интегральных теплот испарения совпадают с аддитивными значениями Второй закон Вревского Закон относится к изменению состава азеотропа при варьировании температуры (давления). Для азеотропа в уравнении (43) 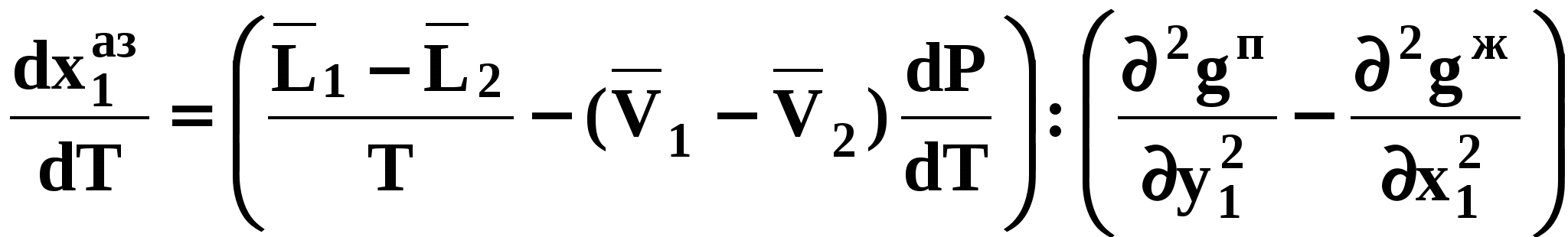 . (47) . (47)Для идеального пара получаем уравнение Сторонкина-Морачевского, которое является математическим выражением второго закона Вревского: 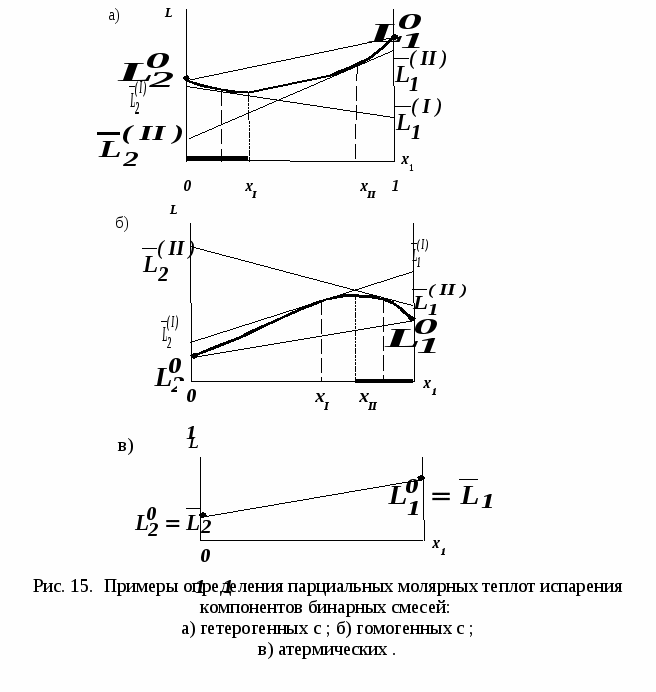 Второй закон Вревского 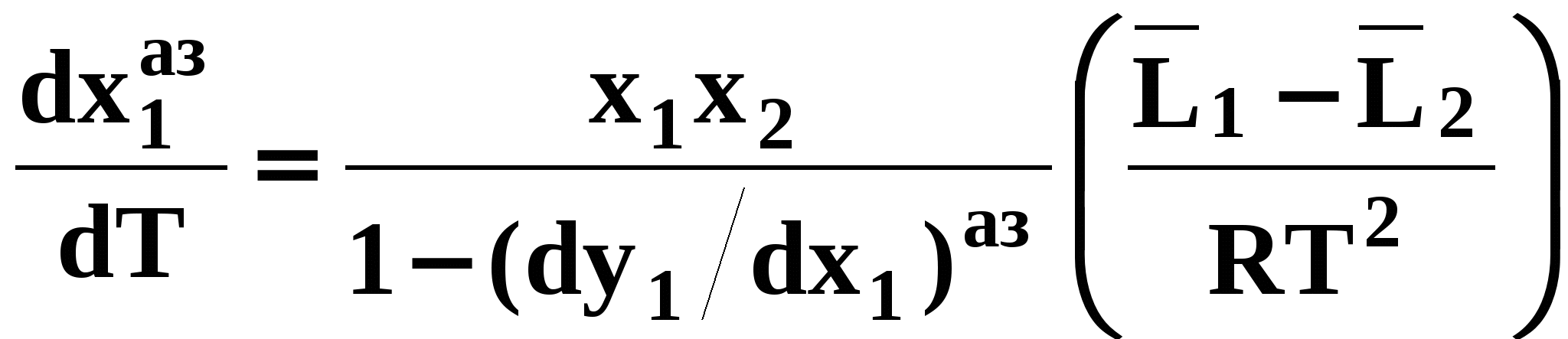 . (48) . (48)Знак производной положительного азеотропа имеем Формулировки второго закона Вревского для азеотропов разных типов: при увеличении температуры (давления) положительный азеотроп обогащается компонентом с большей парциальной молярной теплотой испарения: отрицательный азеотроп обогащается компонентом с меньшей парциальной молярной теплотой испарения: Эволюция бинарного азеотропа, представленная на рис. 16, характеризуется соотношениями: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
