|
|
Раева_Фролкова_Н_2013_end. Основные законы равновесия жидкость пар бинарных систем
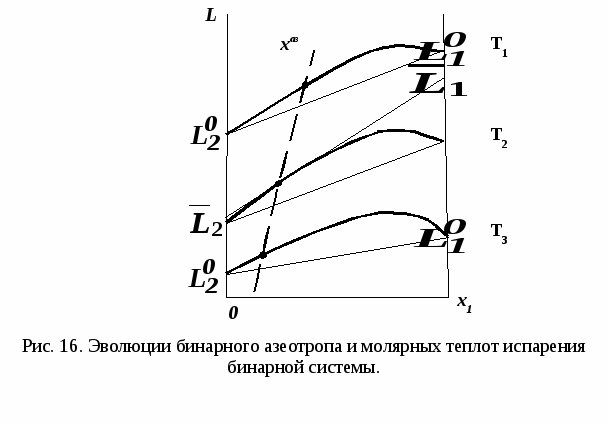
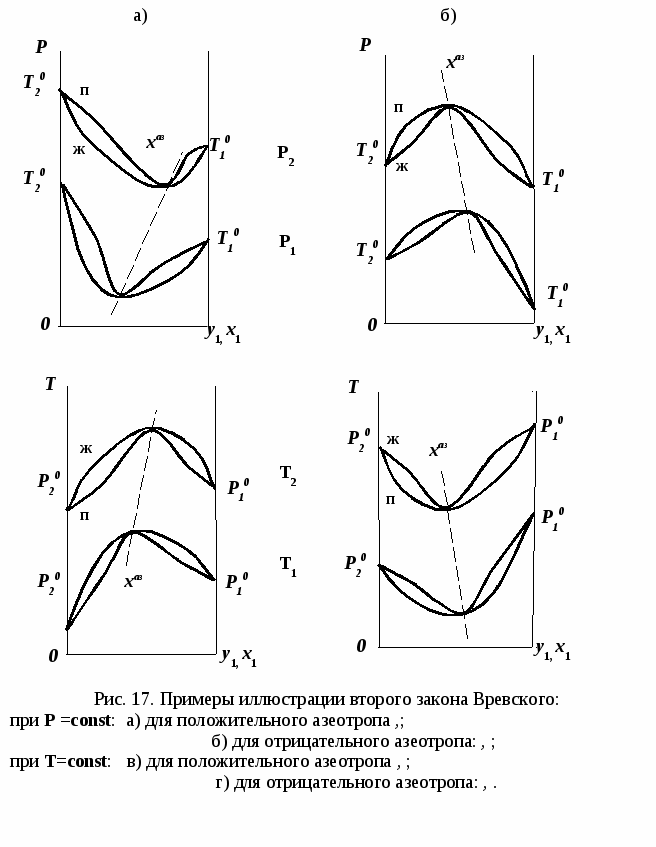
в) г)
Закон охватывает условия второго и первого законов, которые совместимы в бесконечно малый промежуток времени. Первоначально рассматривают точку азеотропа при определенных температуре и давлении (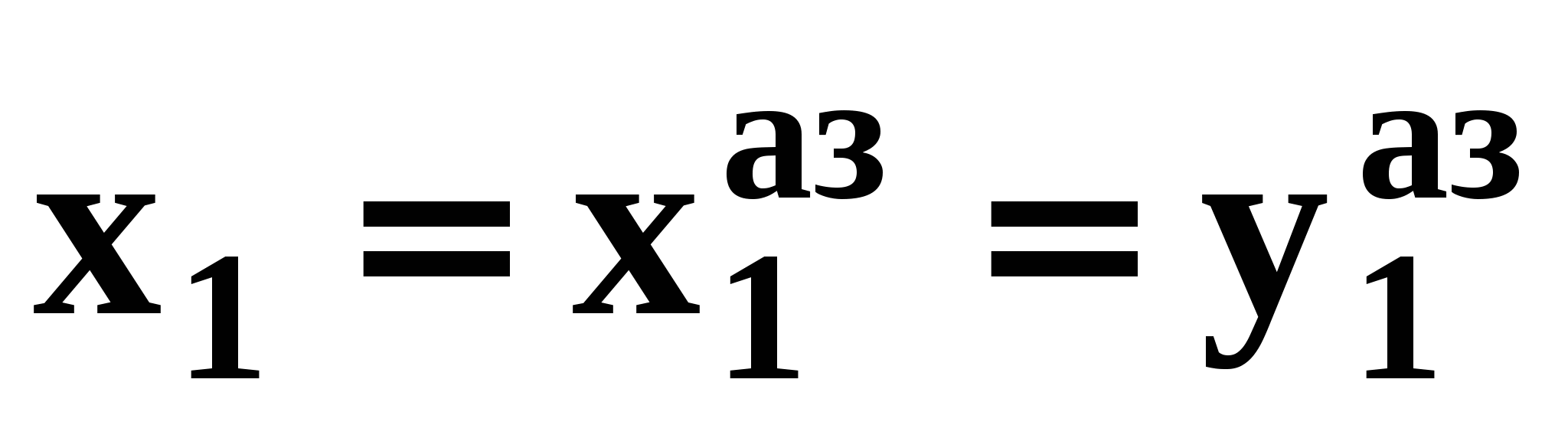 ), далее, закрепив этот состав ( ), далее, закрепив этот состав (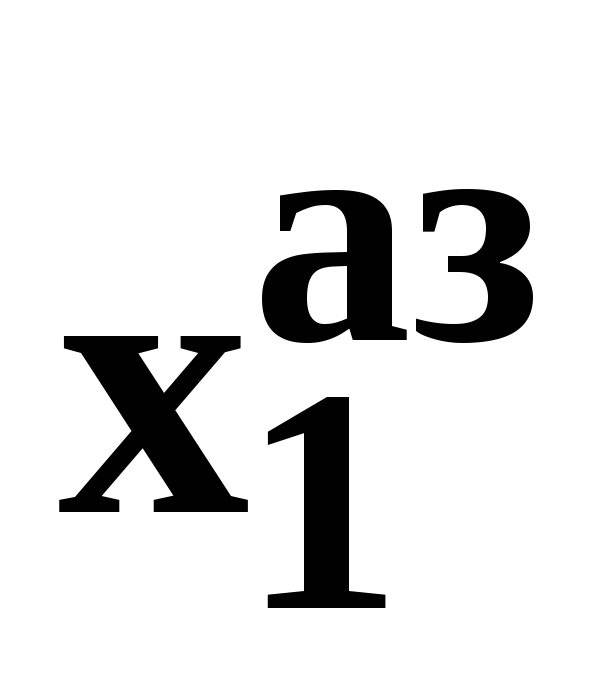 =const), исследуют изменение состава пара и азеотропа при варьировании температуры (давления). Следовательно, в начальный момент можно приравнять выражения в скобках, полученные из уравнений (44) и (47). =const), исследуют изменение состава пара и азеотропа при варьировании температуры (давления). Следовательно, в начальный момент можно приравнять выражения в скобках, полученные из уравнений (44) и (47).
В результате имеем результате имеем связь двух производных, отражающих эволюцию составов паровой фазы 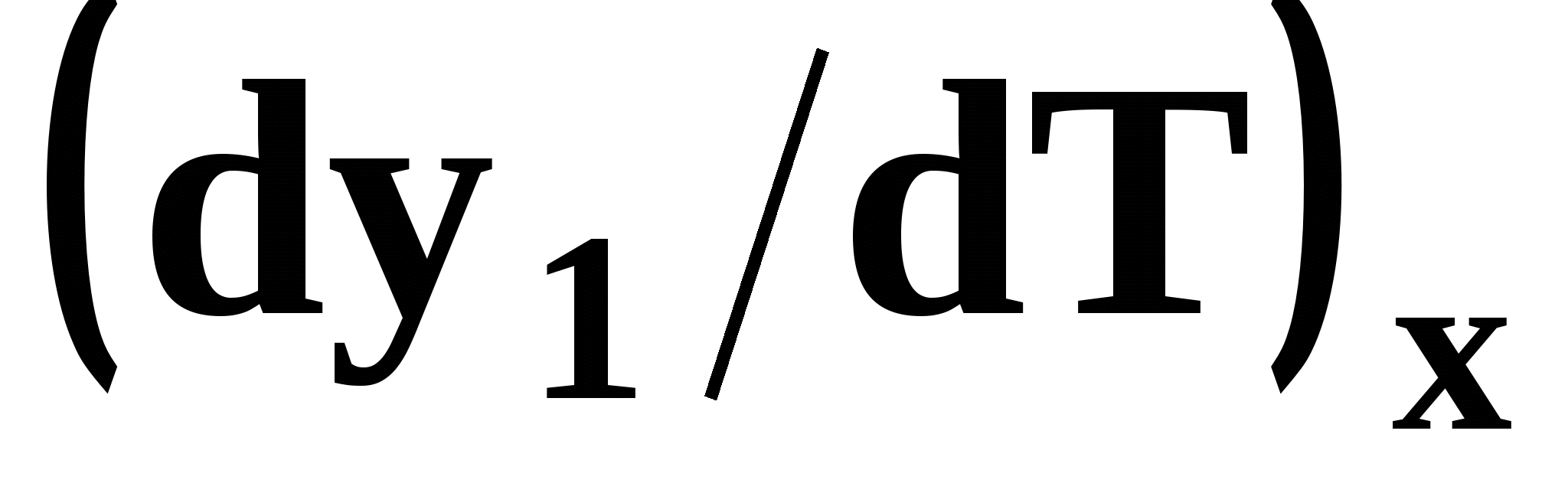 и азеотропа ( и азеотропа (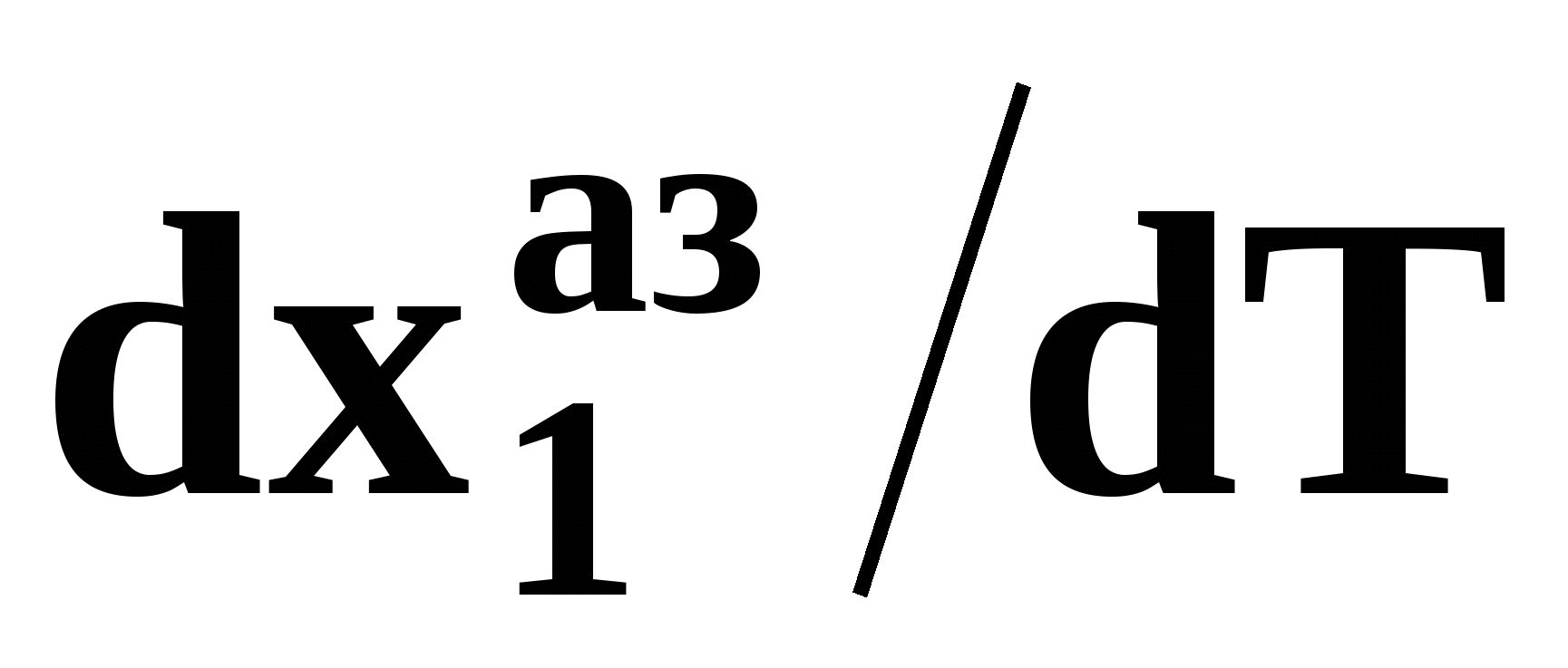 ): ):
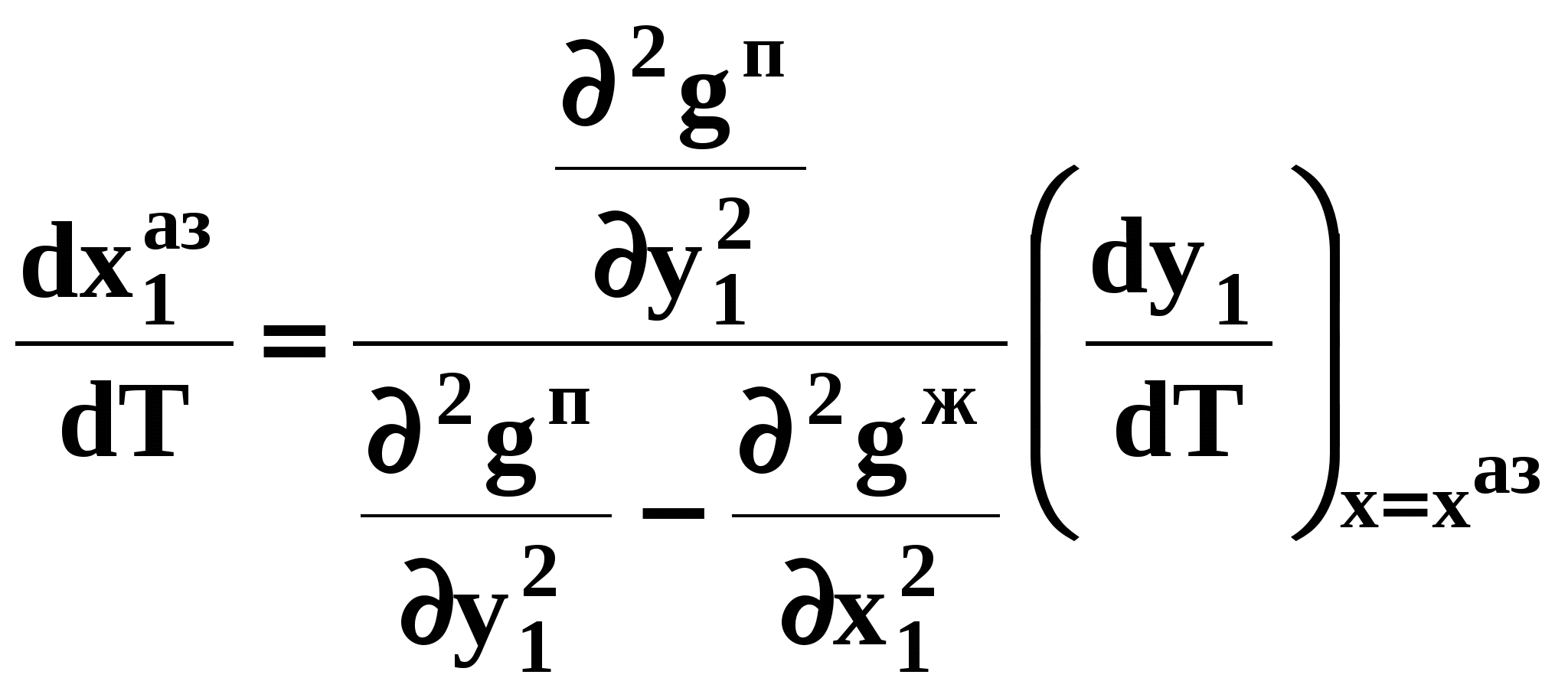 . (49) . (49) Для точки азеотропа из третьего закона Коновалова (37) выразим отношение вторых производных 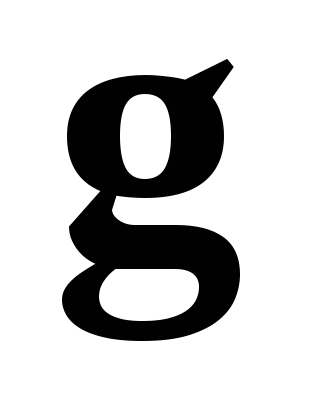 потенциала: потенциала:
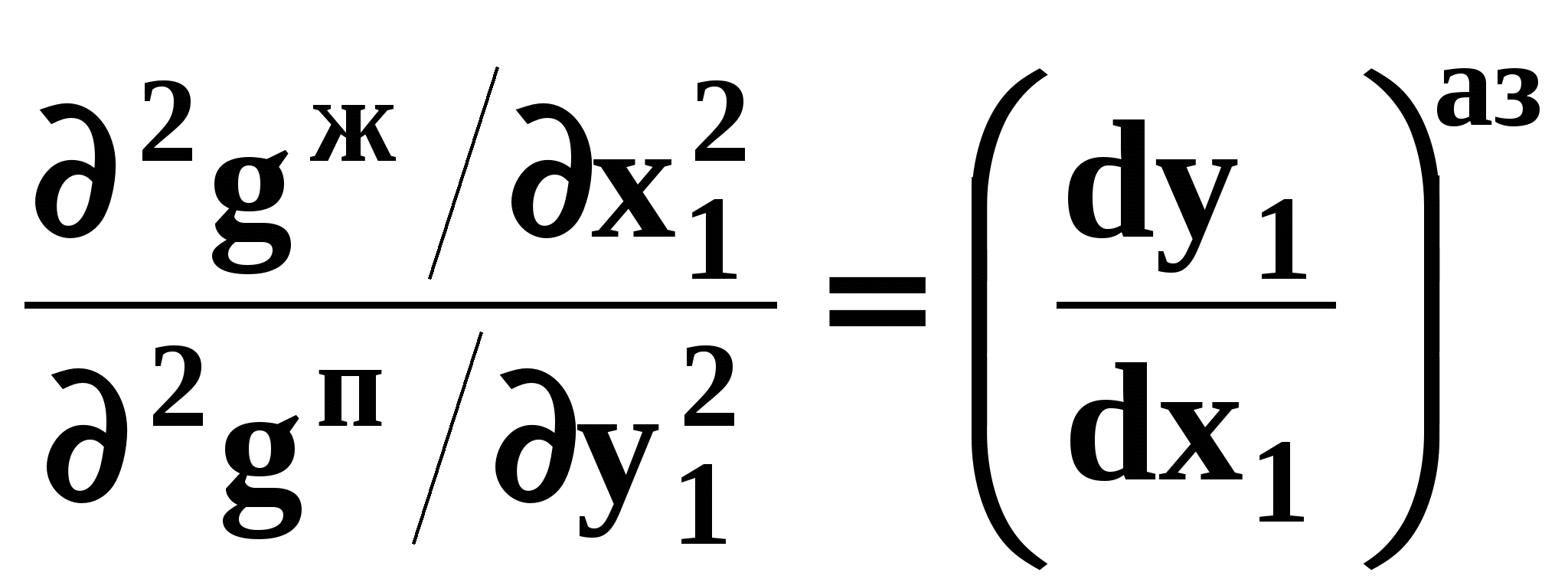 . (50) . (50)
С учетом (48) уравнение (46) имеет вид:
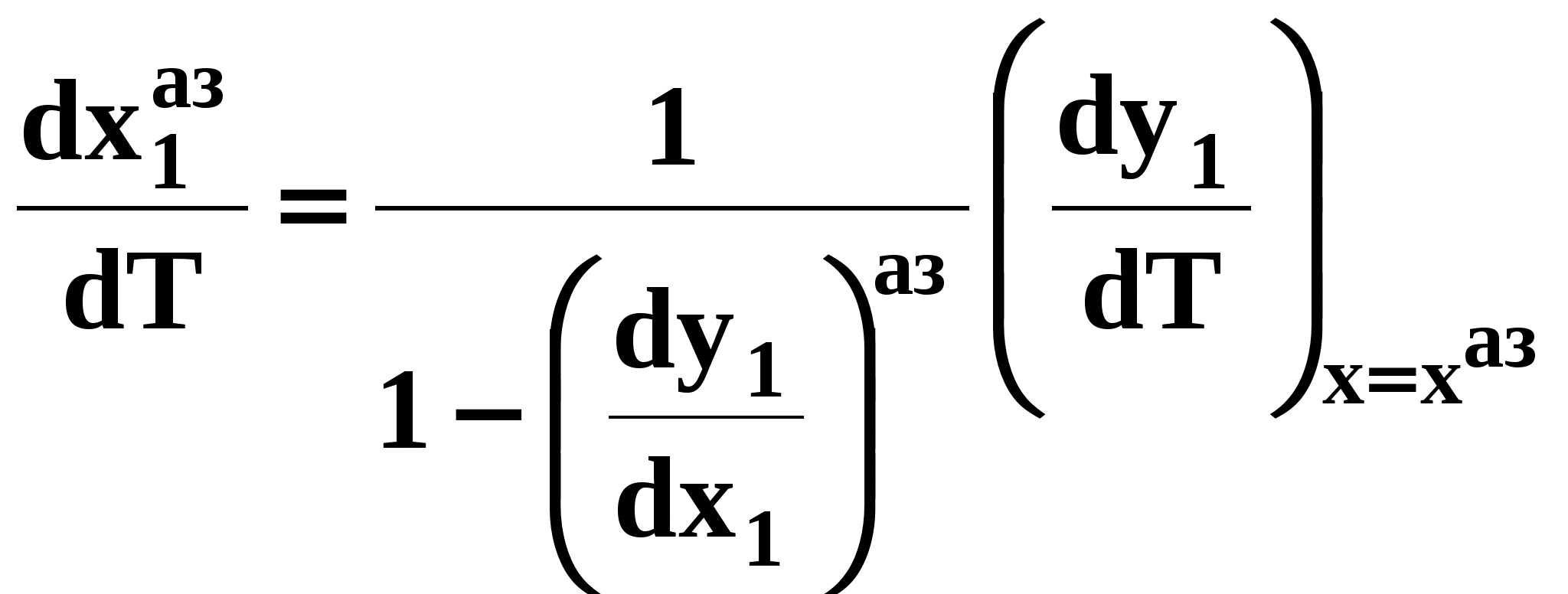 . (51) . (51)
Математический вывод третьего закона Вревского базируется на анализе знаков величин, входящих в уравнение (51). Для положительного азеотропа 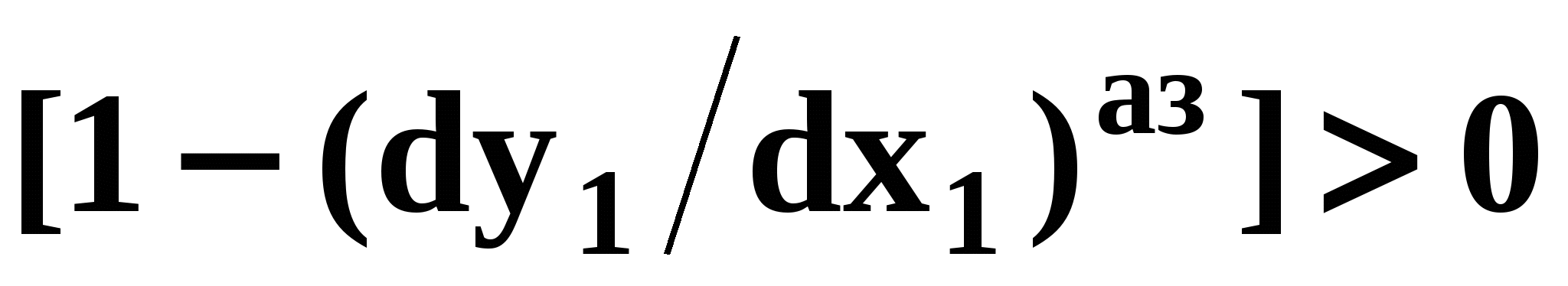 и, следовательно, и, следовательно, 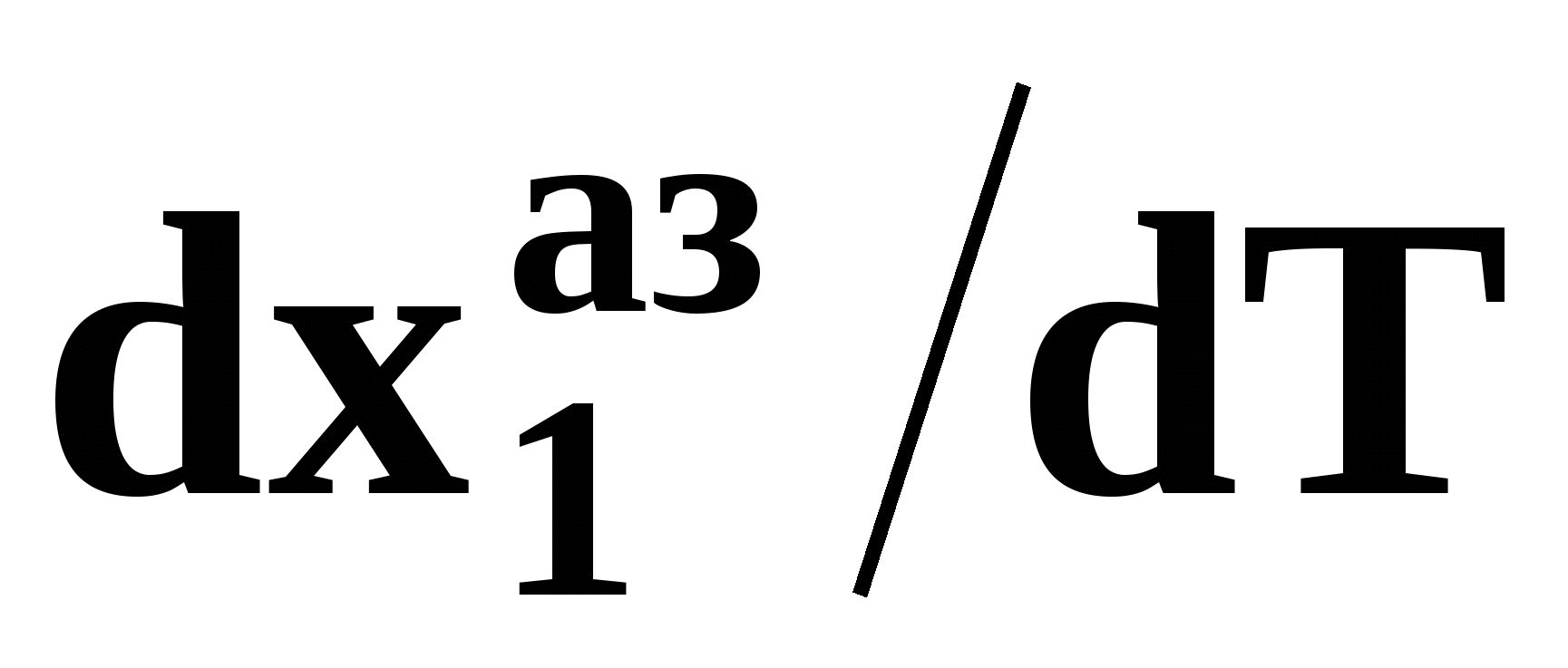 и и 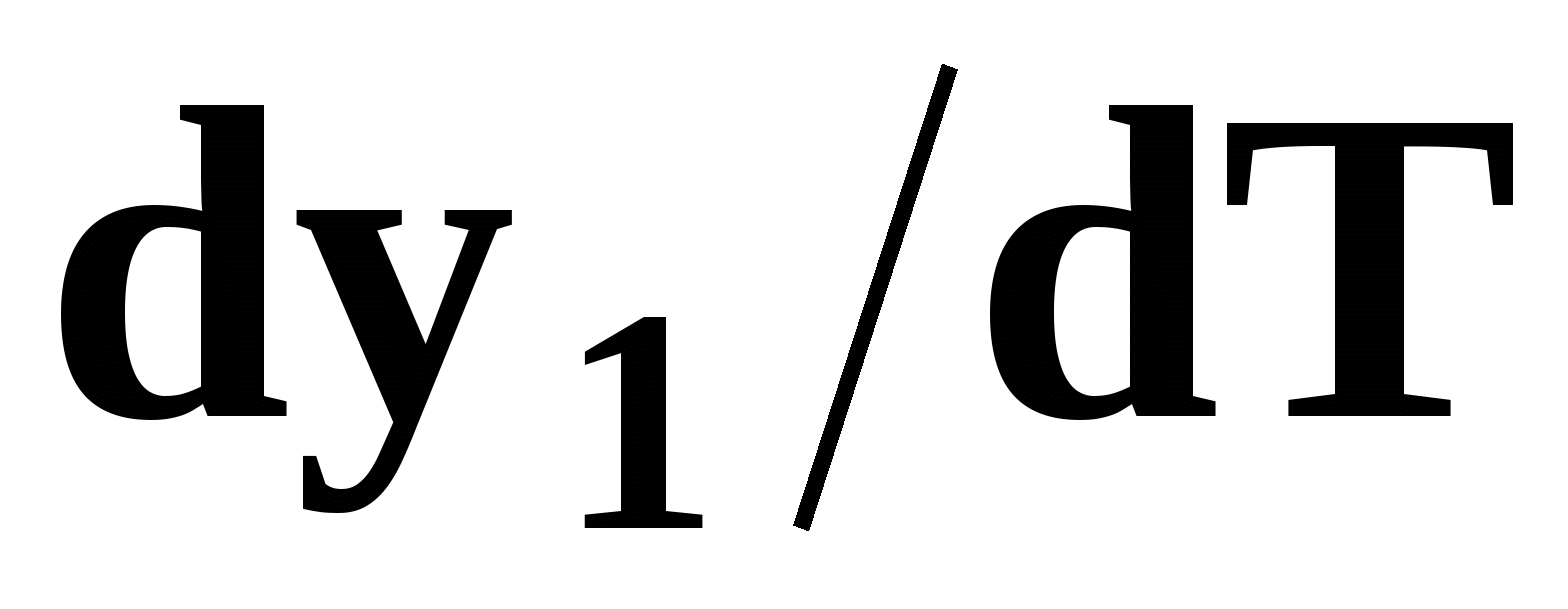 имеют одинаковые знаки. Для отрицательного азеотропа имеют одинаковые знаки. Для отрицательного азеотропа 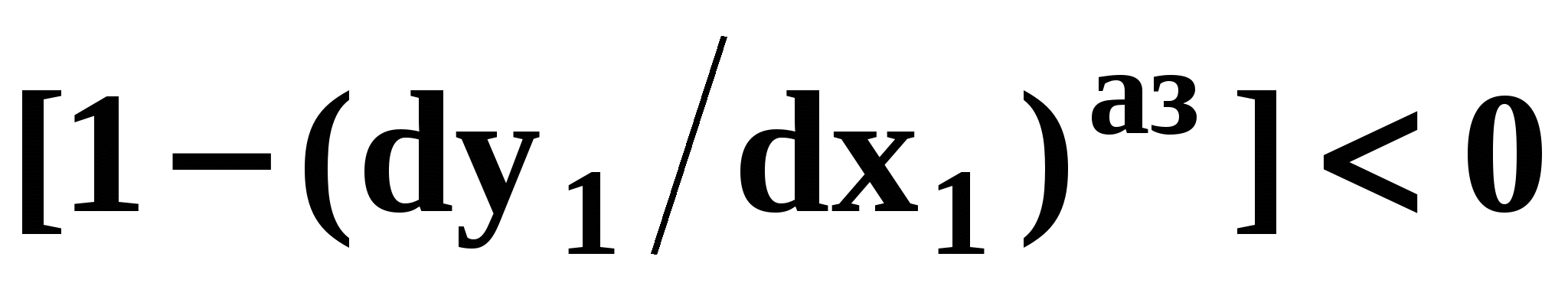 и производные и производные 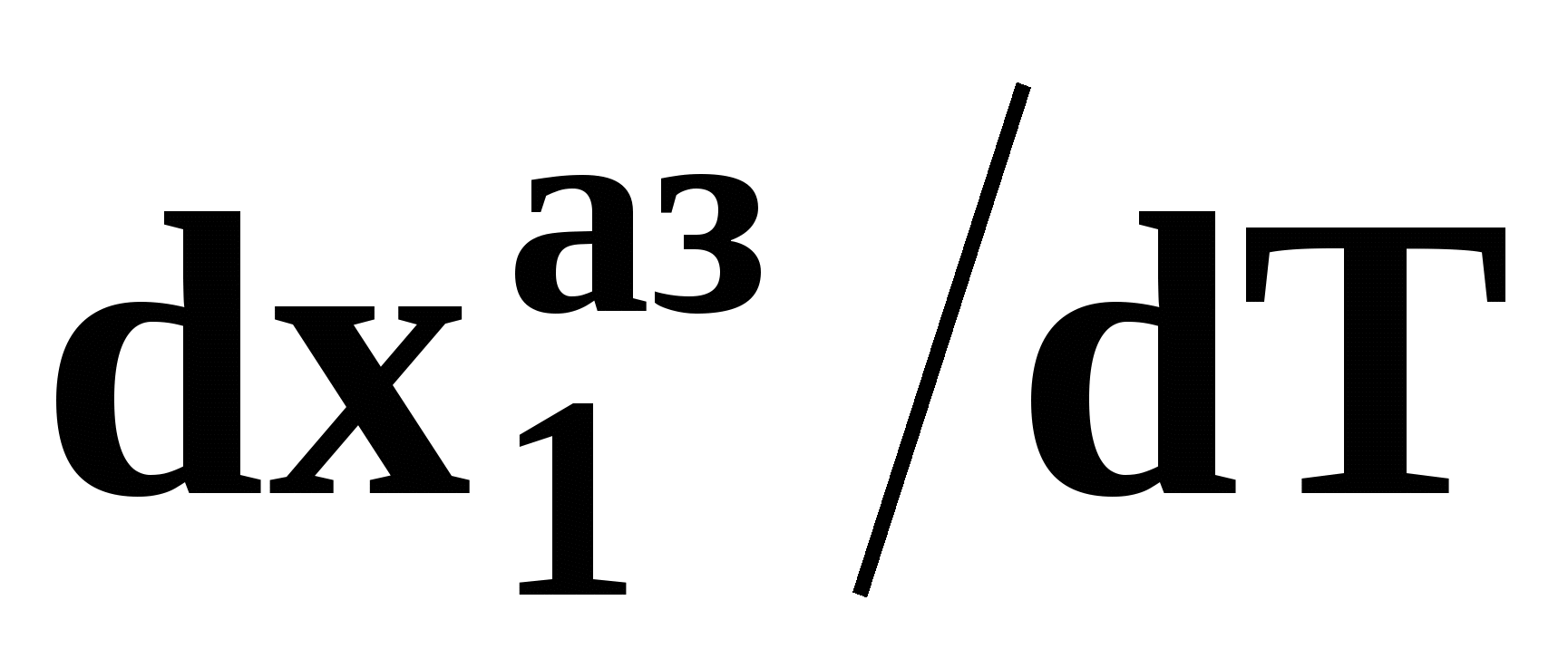 и и 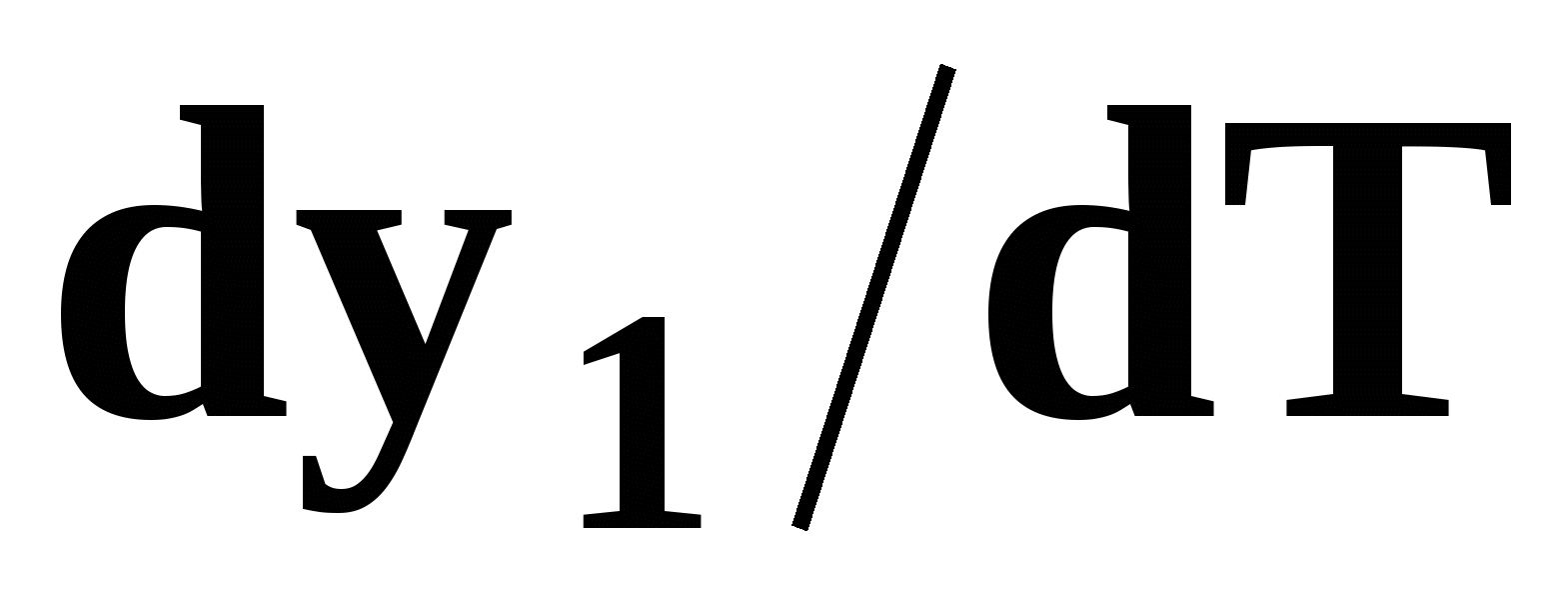 имеют разные знаки. имеют разные знаки.
Формулировка третьего закона Вревского: при увеличении температуры (давления) и для закрепленного состава жидкой фазы
для положительного азеотропа изменение составов пара и азеотропа происходит однонаправленно;
для отрицательного азеотропа изменение составов пара и азеотропа происходит разнонаправленно.
Проиллюстрируем действие закона в графическом виде. В системе с положительным азеотропом (рис. 18а) при увеличении температуры (давления) состав азеотропа обогащается компонентом 1. Для закрепленного состава жидкой фазы в паровой фазе также увеличивается содержание этого компонента (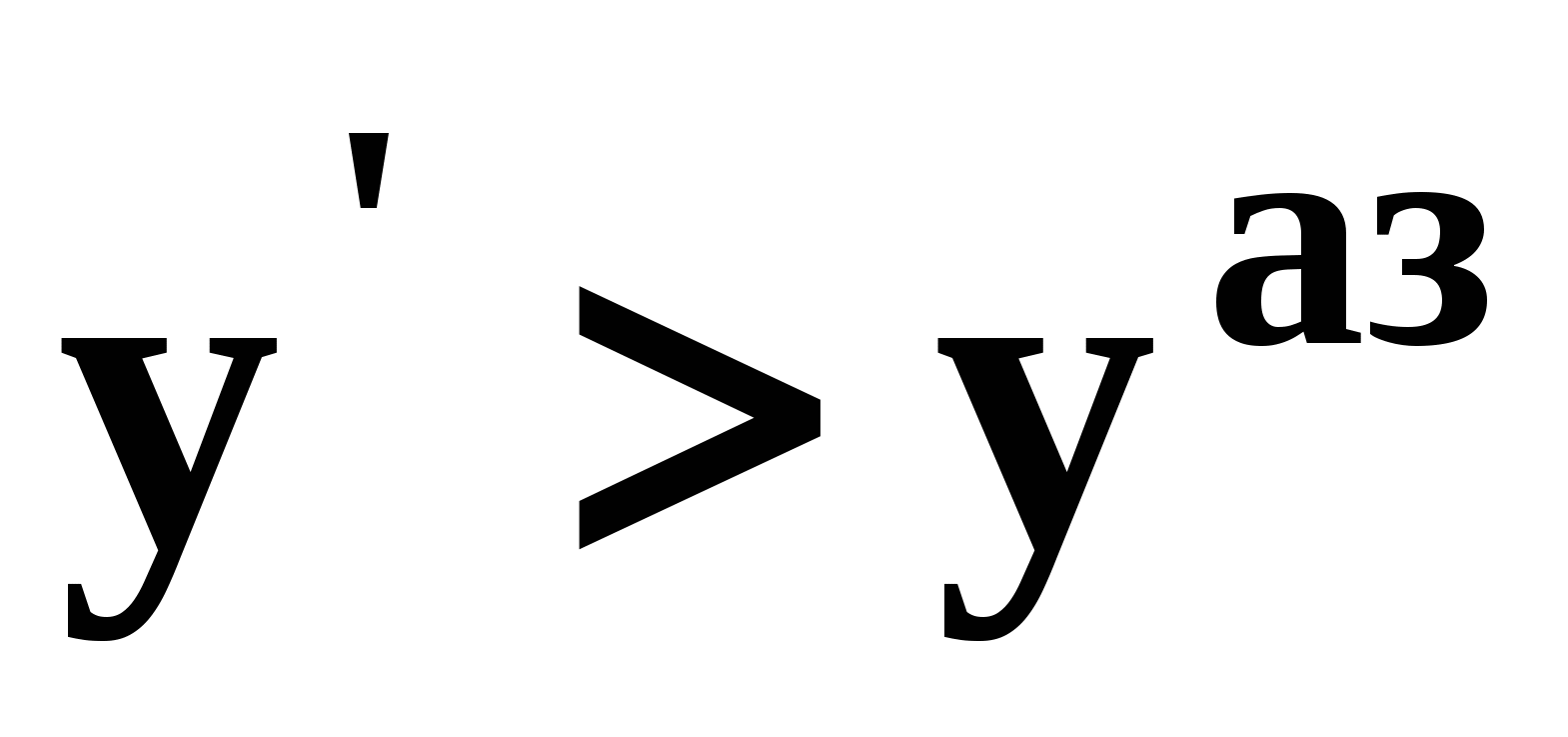 ). В системе с отрицательным азеотропом (рис. 18б) имеем иную картину: при увеличении температуры (давления) пар обогащается компонентом 2, а азеотроп компонентом 1 (разнонаправленное изменение). ). В системе с отрицательным азеотропом (рис. 18б) имеем иную картину: при увеличении температуры (давления) пар обогащается компонентом 2, а азеотроп компонентом 1 (разнонаправленное изменение).
а) б)
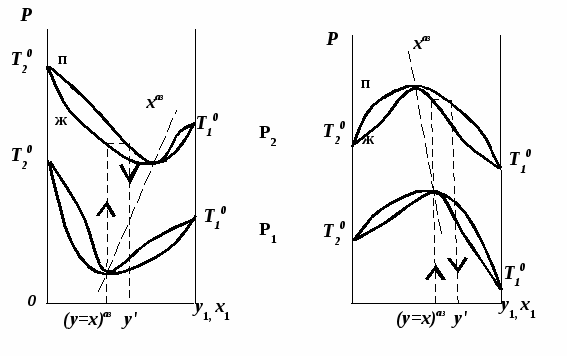
Рис. 18. Графическая интерпретация третьего закона
Вревского в системах с азеотропами разных типов:
а) положительным; б) отрицательным.
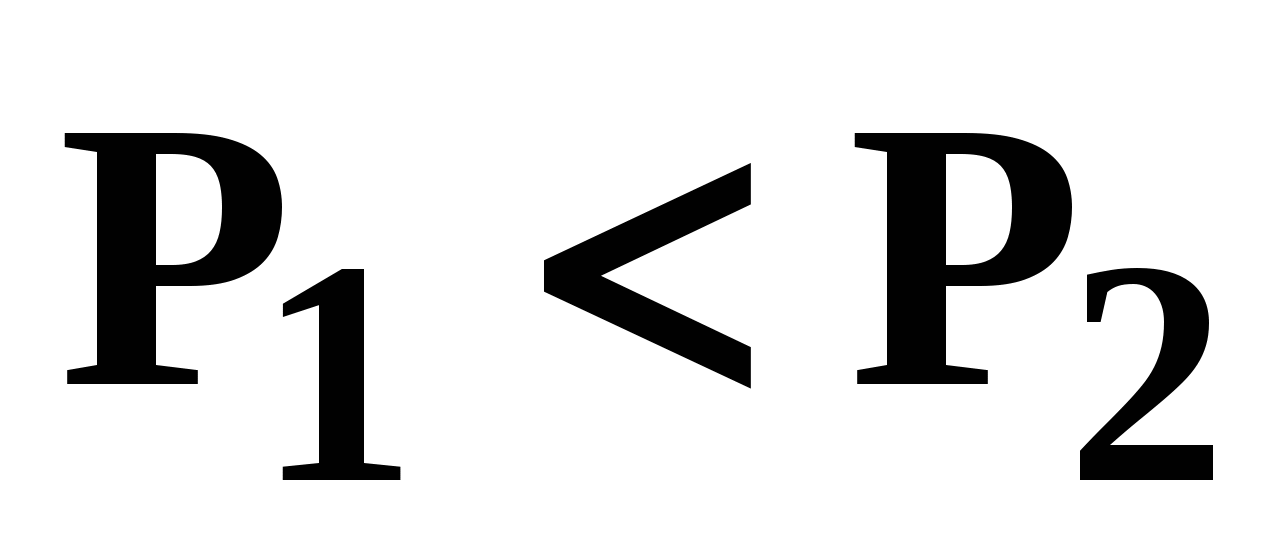
3. Эволюция бинарных азеотропов
Необходимым этапом синтеза возможных вариантов схем разделения азеотропных смесей является анализ физико-химических особенностей поведения системы. Обычной ректификацией в одной колонне не могут быть разделены азеотропные бинарные системы 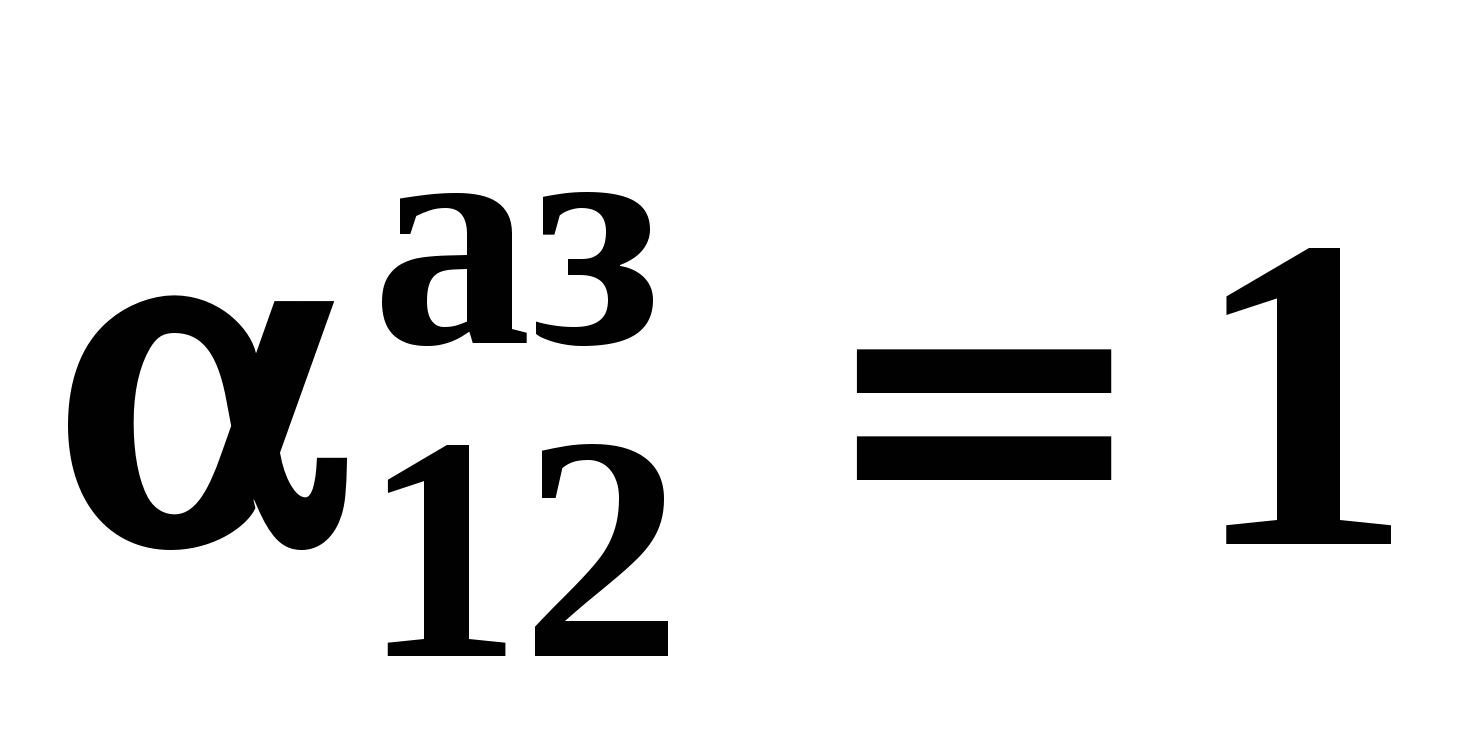 и смеси с и смеси с 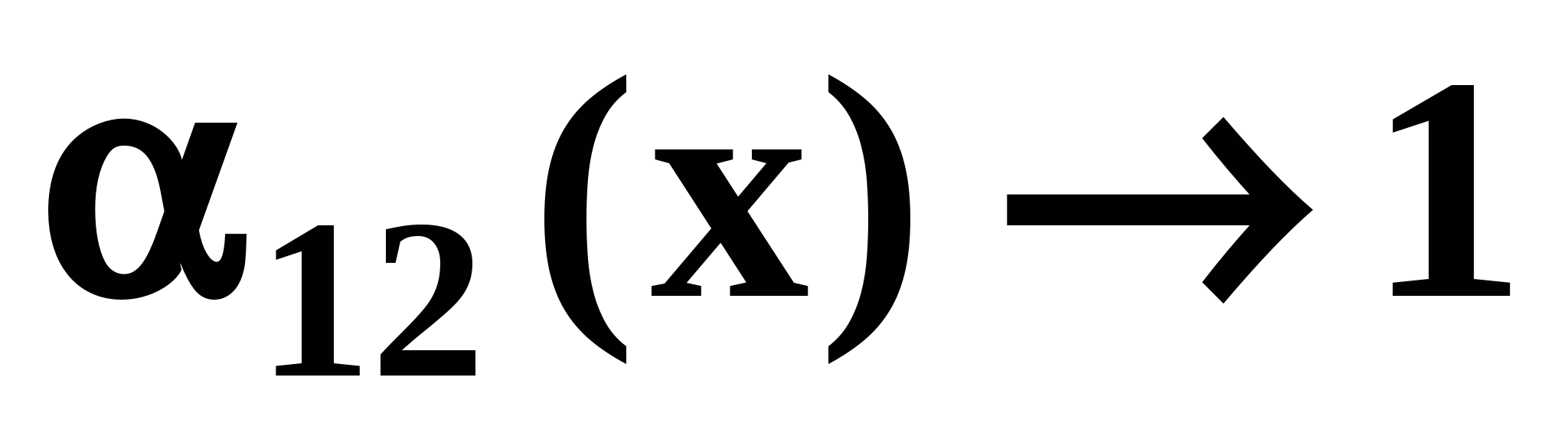 . .
Вывод о наличии либо отсутствии азеотропа можно сделать на основании экспериментальных данных (рис. 11-13). Особенности эволюции бинарных азеотропов (характер изменения составов азеотропов при варьировании внешних условий) учитываются при выборе специального метода ректификации.
Н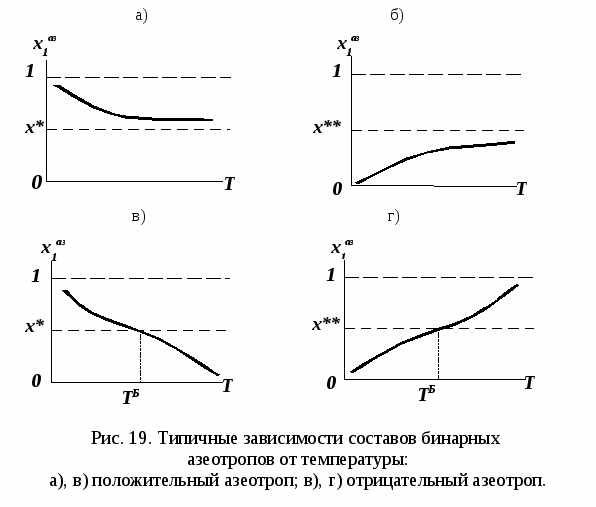 а рис. 19 приведены основные виды зависимостей составов бинарных азеотропов от температуры а рис. 19 приведены основные виды зависимостей составов бинарных азеотропов от температуры 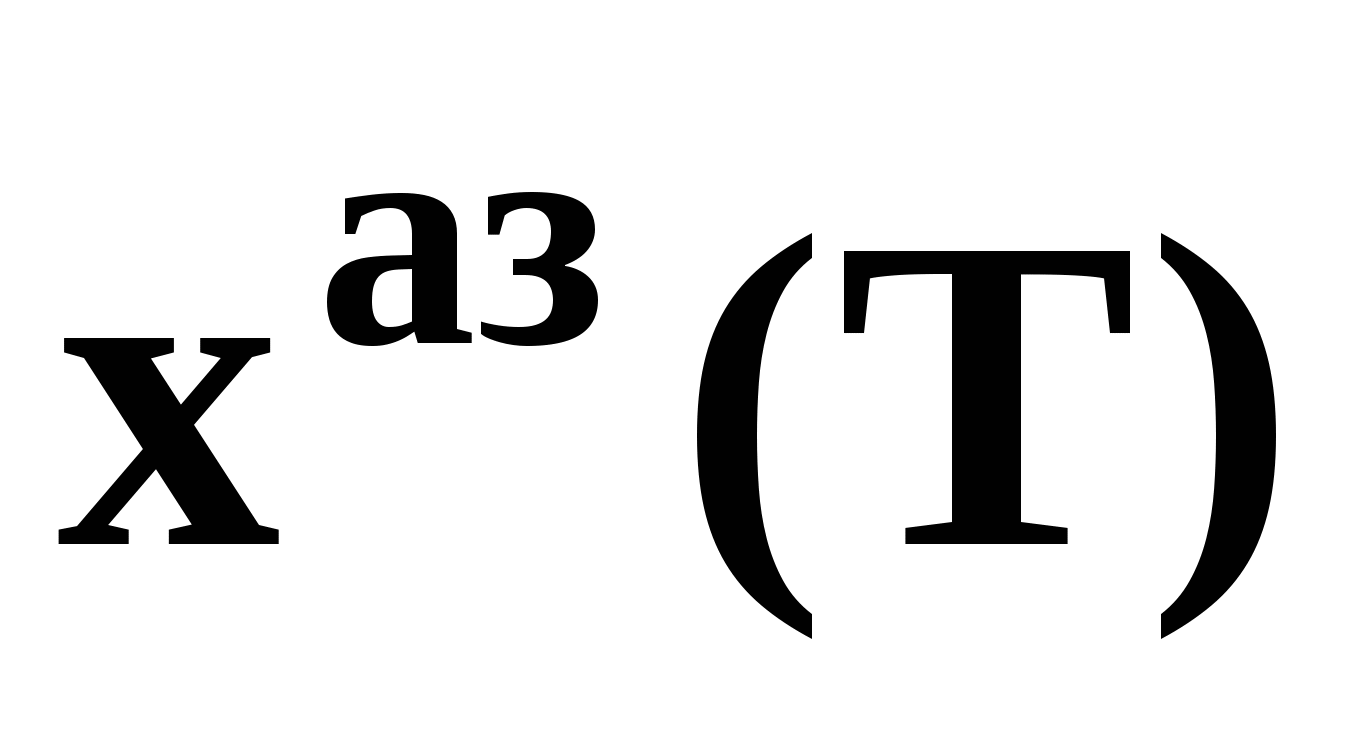 . Зависимости . Зависимости 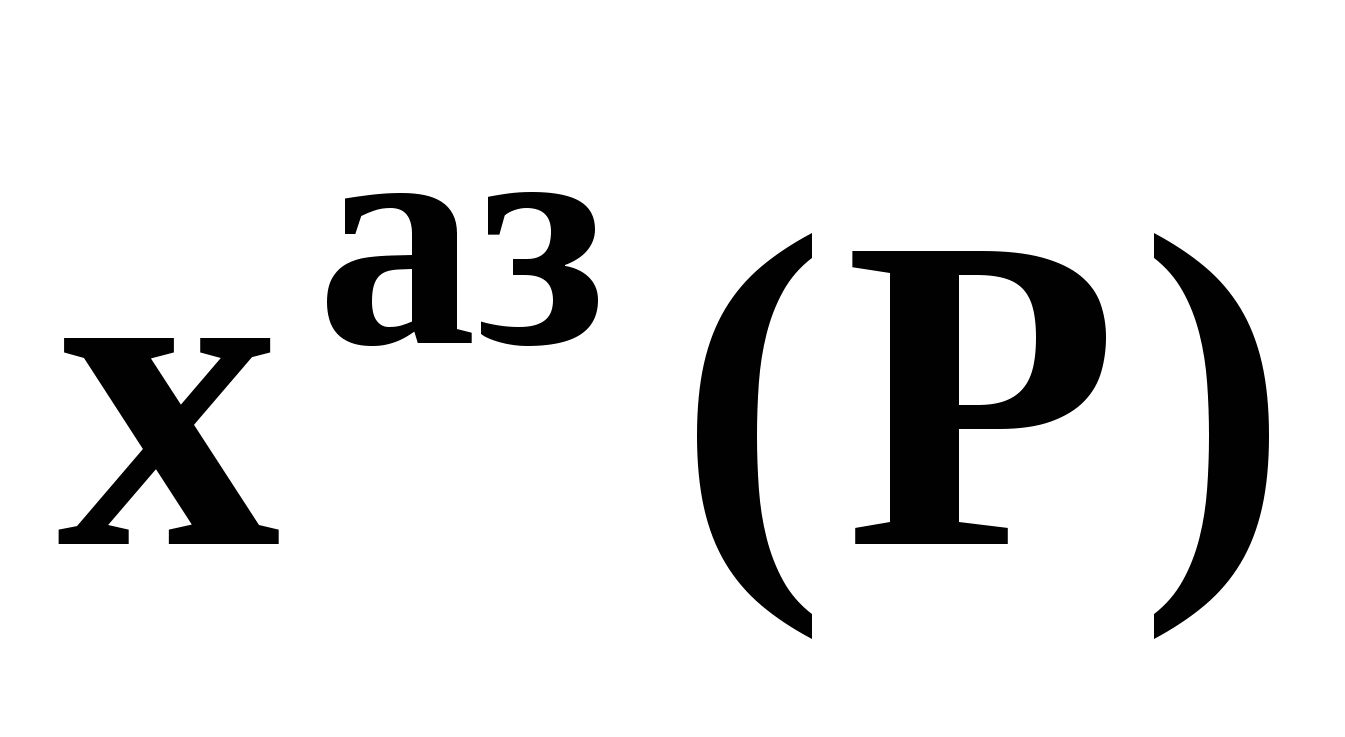 качественно аналогичны. ТБ – температура реализации условия Банкрофта: качественно аналогичны. ТБ – температура реализации условия Банкрофта: 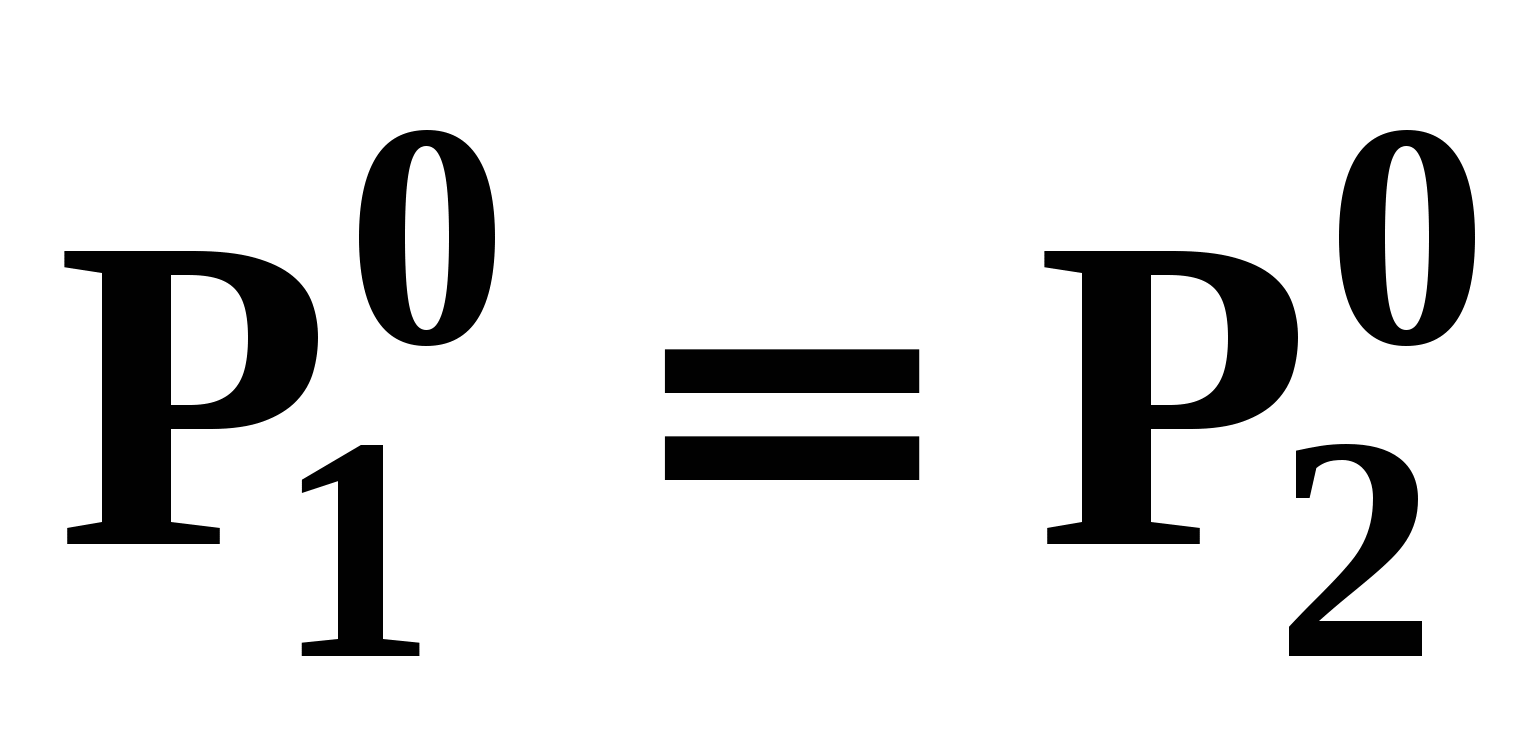 (рис. 20а). (рис. 20а).
1
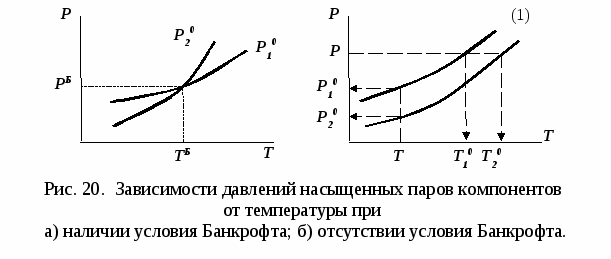
а) б)
(2)
При отсутствии условия Банкрофта компонент 1 во всем диапазоне условий существования равновесия жидкость – пар является легкокипящим: при постоянном давлении его температура кипения меньше 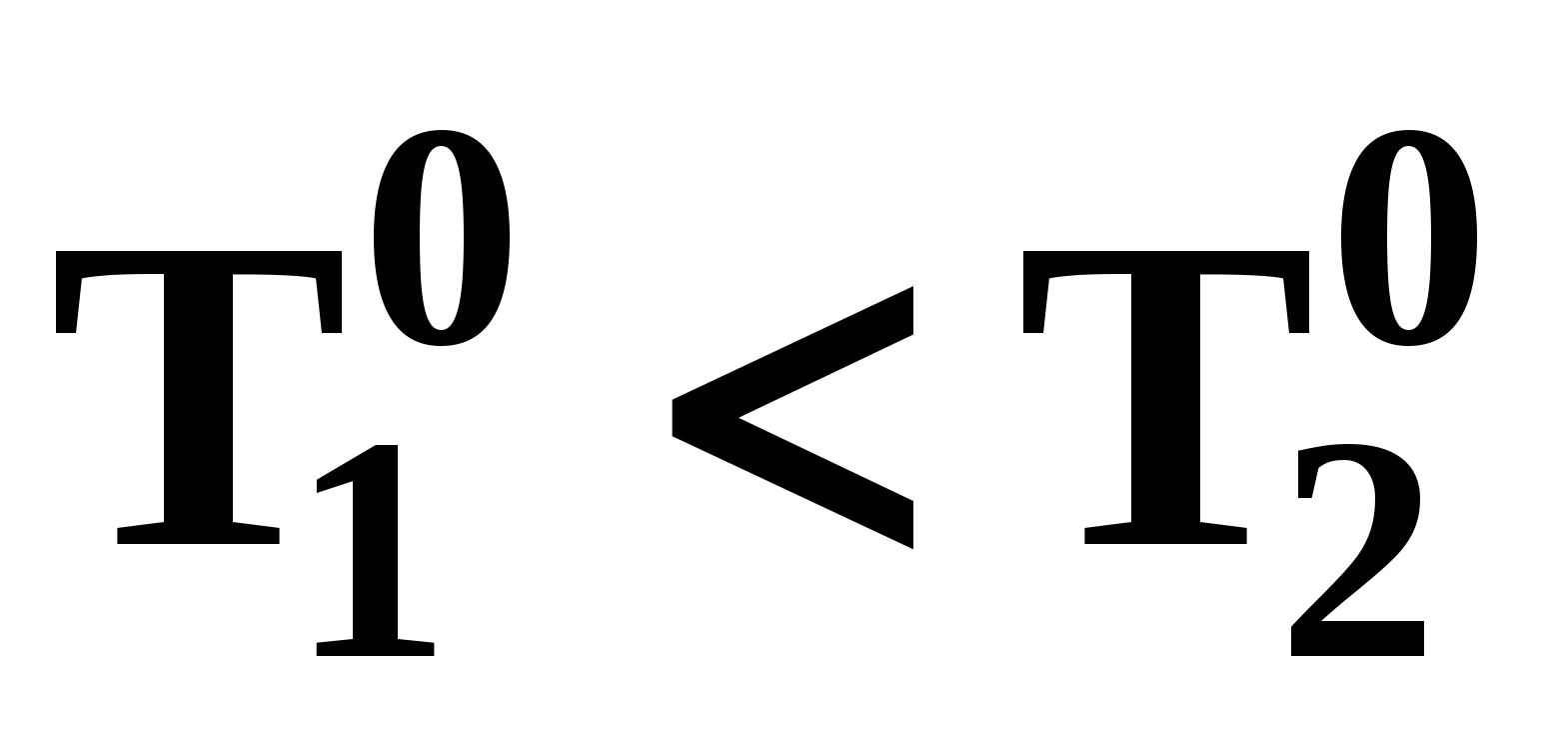 , и легколетучим, т.к. при постоянной температуре давление его насыщенных паров выше , и легколетучим, т.к. при постоянной температуре давление его насыщенных паров выше 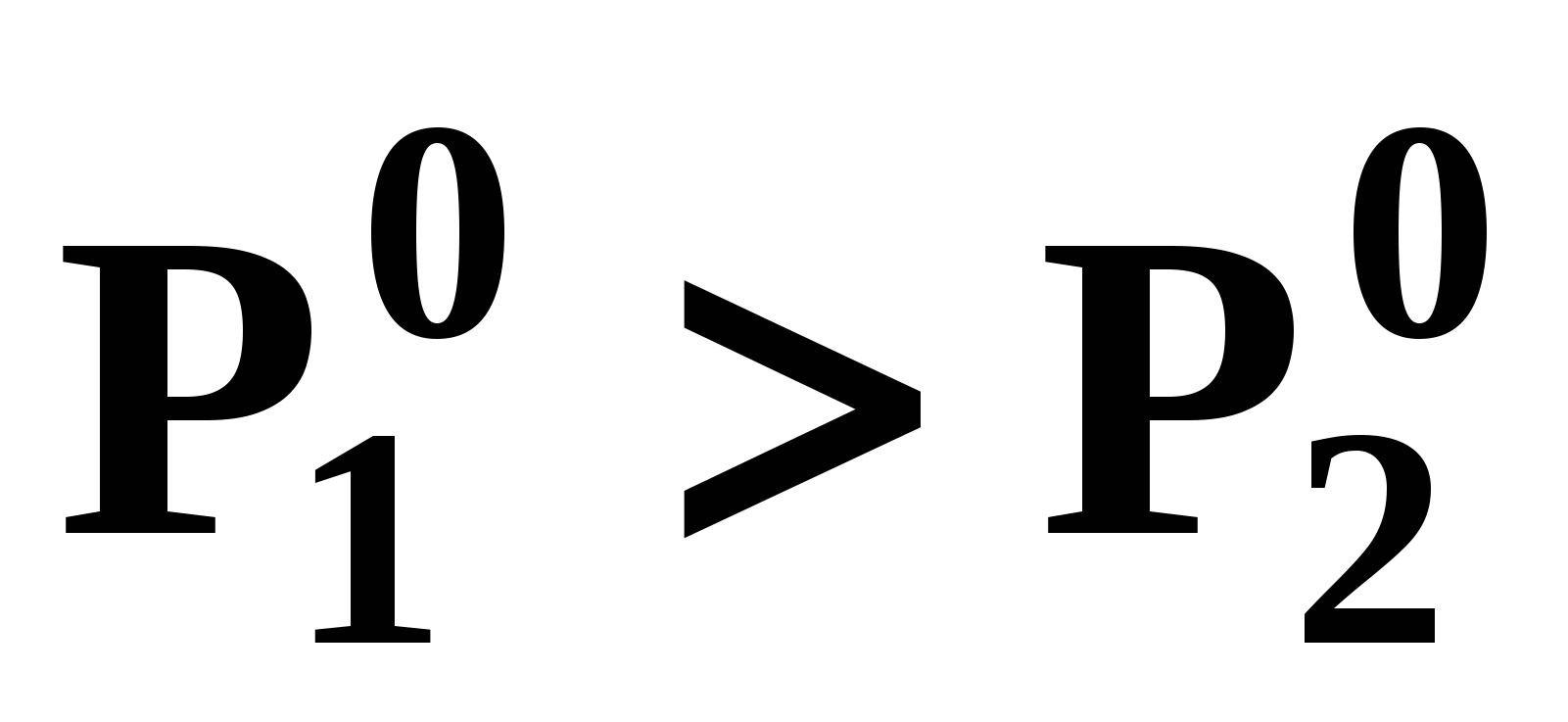 (рис. 20б). (рис. 20б).
При отсутствии в системе условия Банкрофта ТБ бинарный азеотроп расположен между точкой чистого компонента и псевдоидеальной точкой:
- положительный – между точкой легкокипящего компонента 1 и псевдоидеальной точкой 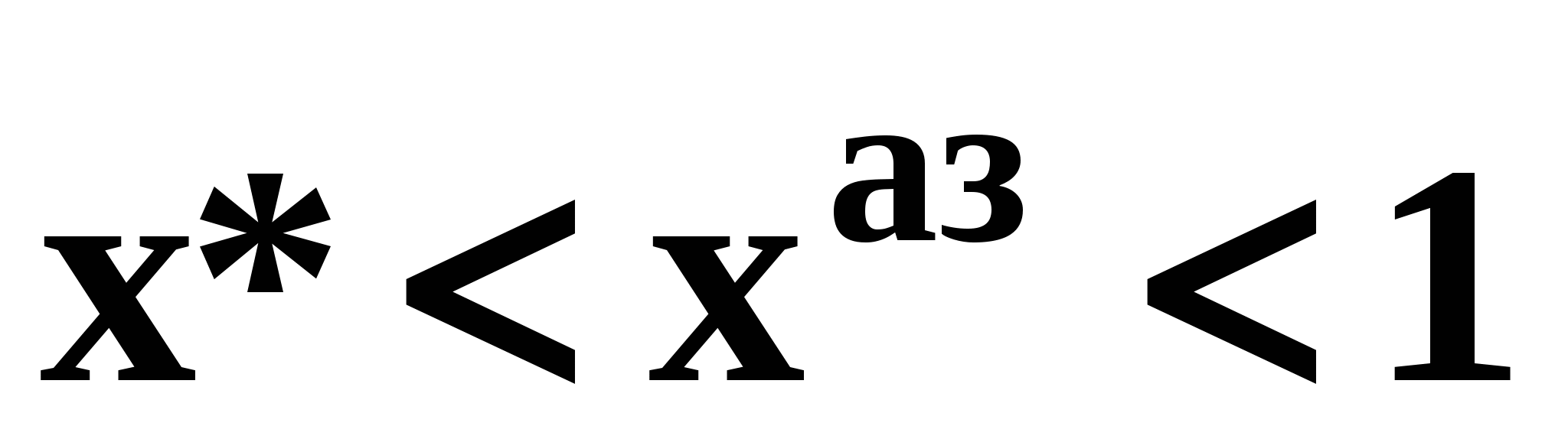 (рис. 19а), (рис. 19а),
- отрицательный – между точкой тяжелокипящего компонента 2 и псевдоидеальной точкой 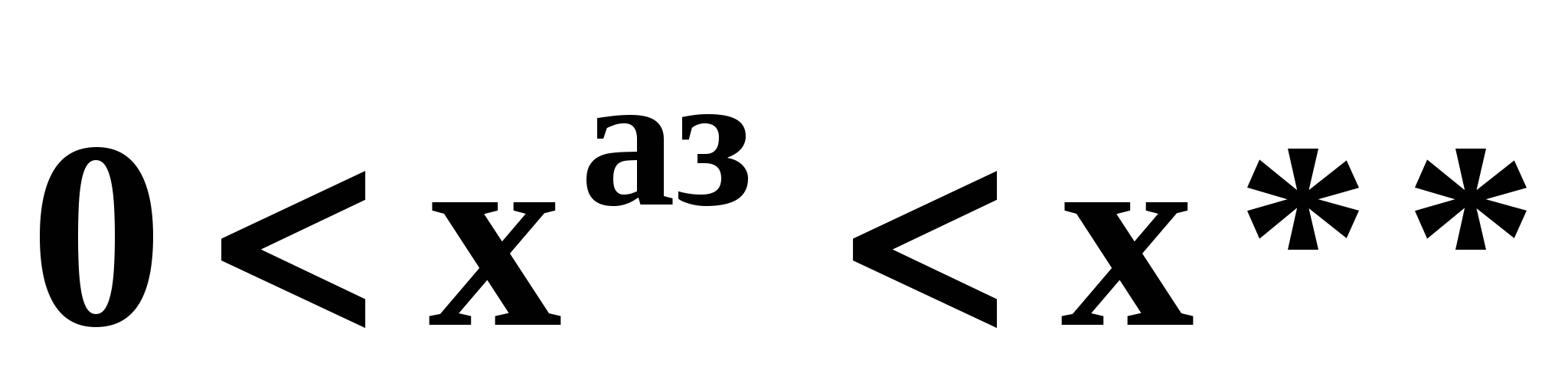 (рис. 19б). (рис. 19б).
Только при наличии в системе точки Банкрофта бинарный азеотроп может при изменении давления «проходить» весь концентрационный диапазон. Азеотроп может «исчезнуть» в точке чистого компонента, в этом случае бинарная смесь может быть разделена в одной ректификационной колонне (рис. 21 а, б). Однако такие случаи эволюции среди реальных азеотропных систем встречаются редко.
Если при варьировании условий состав азеотропа заметно меняется, то
возможно разделение бинарной азеотропной смеси в типовом комплексе ректификационных колонн, работающих под разным давлением (рис. 21 в, г). Если же состав азеотропа практически не меняется под воздействием давления, то используются другие специальные методы ректификации: экстрактивная (или реэкстрактивная) ректификация, сочетание ректификации и первапорации, ректификации и кристаллизации. Бинарные азеотропные расслаивающиеся смеси разделяют с использованием сепараторов и ректификационных колонн.
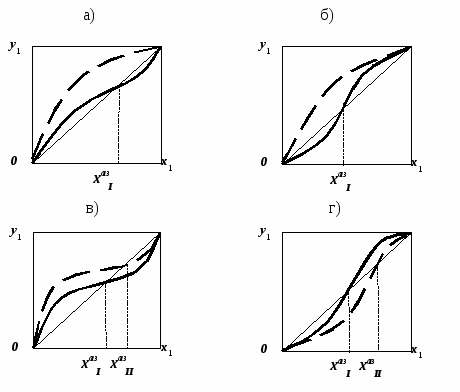
Рис. 21. Преобразование диаграмм у – х бинарных систем
при изменении давления (РI; РII):
а), б) положительные отклонения от идеального поведения;
в), г) отрицательные отклонения от идеального поведения.
Особенности эволюции бинарных биазеотропных систем подробно изложены в [7]. Поведение реальных объектов весьма многообразно. Более сложные примеры фазового поведения бинарных систем и эволюции азеотропов рассматриваются в специальной литературе, однако и в этих случаях справедливы законы парожидкостного равновесия, рассмотренные в данном пособии.
УСЛОВНЫЕ ОБОЗНАЧЕНИЯ И СОКРАЩЕНИЯ
-
Т
|
температура, К
|
Р
|
давление, Па
|
х
|
состав жидкой фазы, м.д.
|
у
|
состав паровой фазы, м.д.
|
k
|
коэффициент распределения компонента
|
|
относительная летучесть компонентов
|
|
коэффициент фугитивности компонента
|
|
коэффициент активности компонента
|
|
химический потенциал компонента
|
|
число фаз
|
f
|
число степеней свободы
|
n
|
число компонентов
|
L
|
молярная теплота испарения, Дж/моль
|
S
|
энтропия, Дж/К
|
g
|
молярная энергия Гиббса, Дж/моль
|
h
|
молярная энтальпия, Дж/моль
|
s
|
молярная энтропия, Дж/(моль К)
|
v
|
молярный объем, м3/моль
|
Индексы
|
аз
|
азеотроп
|
ид
|
|
кр
|
критическая точка
|
ж
|
жидкая фаза
|
п
|
паровая фаза
|
с
|
критические условия
|
тв
|
твердая фаза
|
ф
|
фаза
|
э
|
эвтектика
|
0
|
чистое вещество
|
1, 2, i
|
компоненты
|
Е
|
избыточное термодинамическое свойство
|
Сокращения
|
ВКТР
|
верхняя критическая точка растворимости
|
НКТР
|
нижняя критическая точка растворимости
|
ПЖР
|
парожидкостное равновесие
|
ЛИТЕРАТУРА
1. Термодинамика равновесия жидкость – пар / Под ред. А.Г. Морачевского. – Л.: Химия, 1989. 344 с.
2. Людмирская Г.С., Барсукова Т.В., Богомольный А.М. Равновесие жидкость пар. Справочник. Л.: Химия, 1987. 336 с.
3. Коган В.Б., Фридман В.М., Кафаров В.В. Равновесие между жидкостью и паром. Справочное пособие, в 2-х томах. М.-Л.: Наука, 1966. 1440 с.
4. Огородников С.К., Лестева Т.М., Коган В.Б. Азеотропные смеси. Справочник. Л.: Химия, 1971. 848 с.
5. Gmehling J., Onken U., Rarey J.R. Vapor-Liquid Equilibrium Data Collection. Published by DECHEMA. Editors: Reiner Eckermann, Gerhard Kreysa.
6. Решетов С.А. Банк данных по физико-химическим свойствам компонентов и их смесей RSA DB. Методическое пособие. – М.МИТХТ, 2007. 32 с.
7. Челюскина Т.В., Серафимов Л.А. Закономерности поведения бинарных биазеотропных систем. Учебное пособие. – М. МИТХТ, 2003. 44 с.
Издание учебное
Раева Валентина Михайловна
Фролкова Анастасия Валериевна
ОСНОВНЫЕ ЗАКОНЫ РАВНОВЕСИЯ ЖИДКОСТЬ – ПАР
БИНАРНЫХ СИСТЕМ
Учебное пособие
Подписано в печать ………………Формат 6084/16. Бумага писчая. Отпечатано на ризографе. Усл. печ. листов ……. Тираж 100 экз. Заказ № ……….
ГОУ ВПО «Московский государственный университет тонких химических технологий имени М.В. Ломоносова»
Издательско-полиграфический центр
119571, Москва, пр. Вернадского, 86.
|
|
|
 Скачать 1.12 Mb.
Скачать 1.12 Mb.


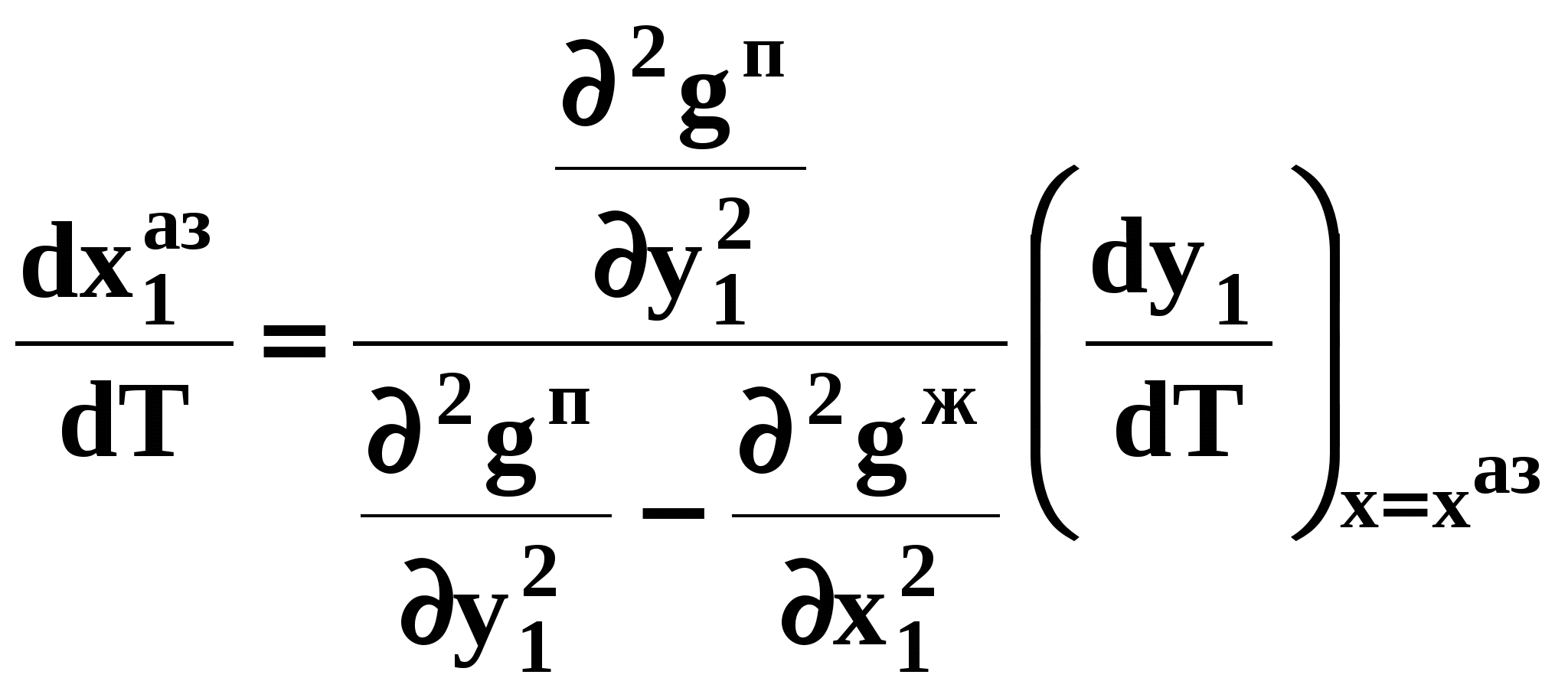 . (49)
. (49)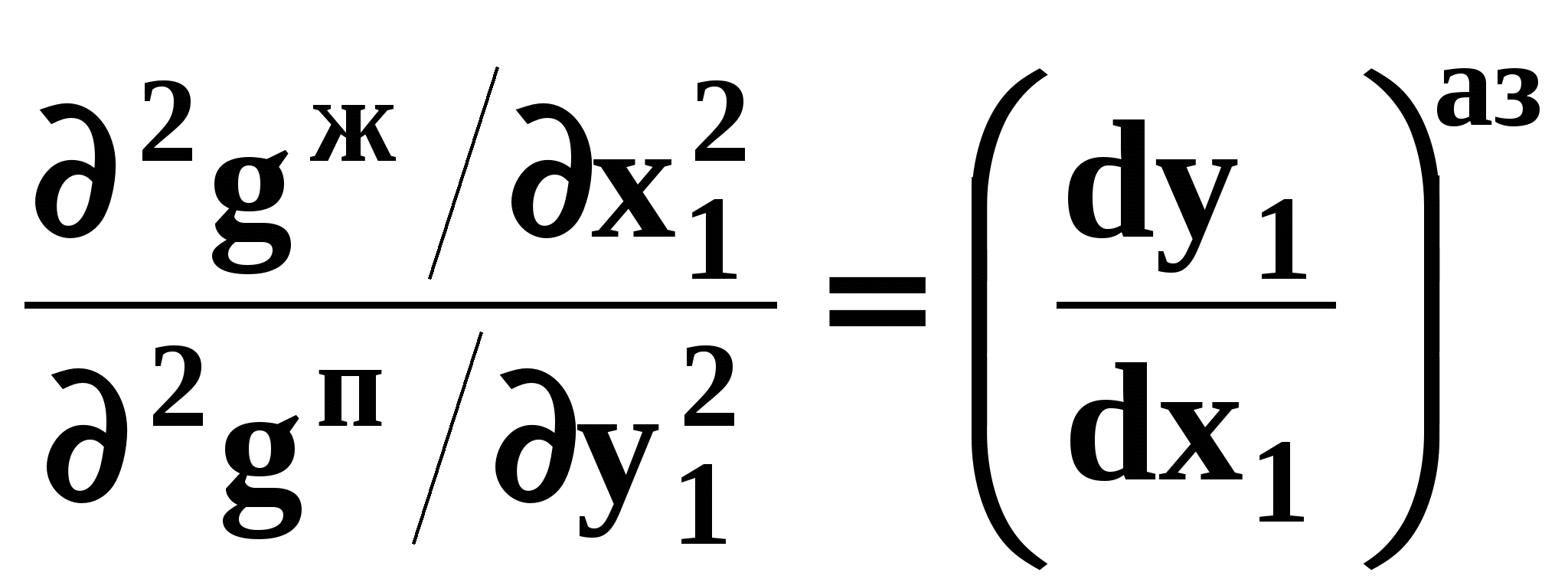 . (50)
. (50)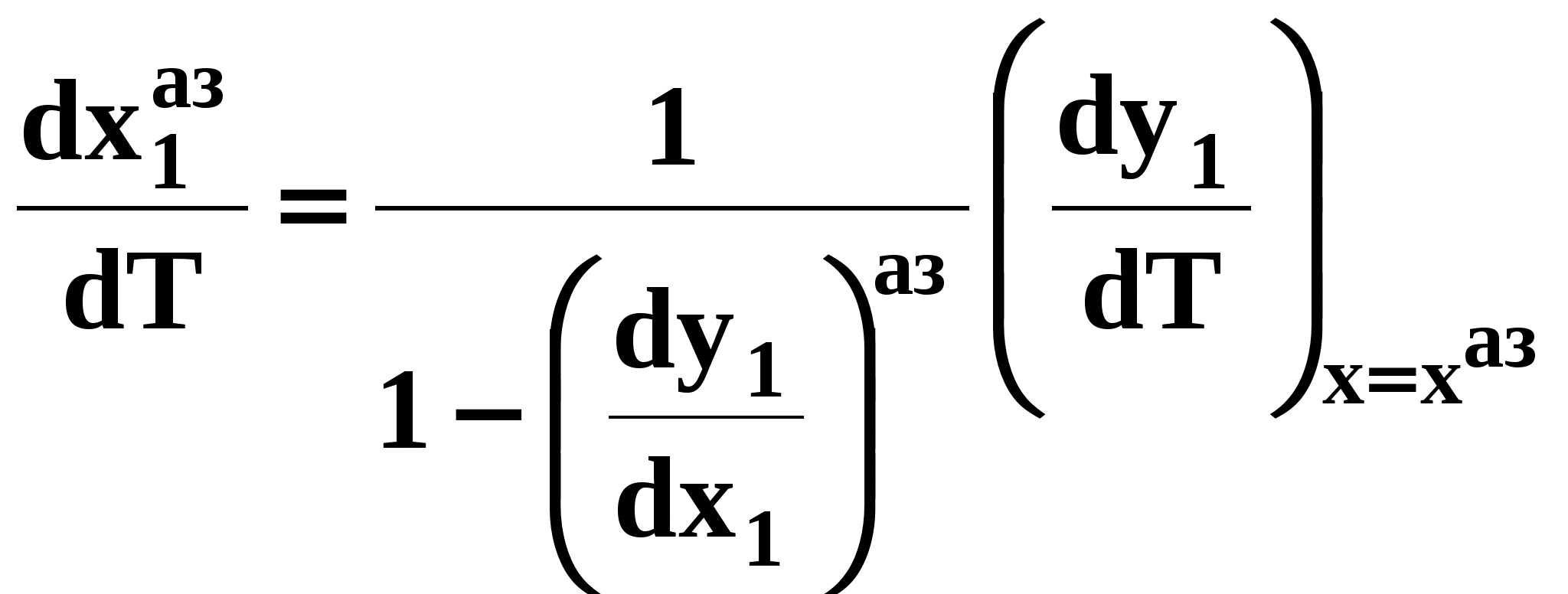 . (51)
. (51)
 а рис. 19 приведены основные виды зависимостей составов бинарных азеотропов от температуры
а рис. 19 приведены основные виды зависимостей составов бинарных азеотропов от температуры 
