Отчёт R Studio Laba6 ZOW. Отчет к лабораторной работе 6 R по дисциплине Интеллектуальный анализ данных Работу
 Скачать 274 Kb.
|
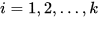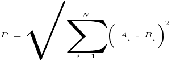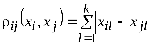                             ФГБОУ ВО Уфимский государственный авиационный технический университет Кафедра Вычислительной математики и кибернетики Отчет к лабораторной работе №6 «R» по дисциплине «Интеллектуальный анализ данных» Работу выполнили студенты группы ПРО-412 Звягинцева И.А. Онищенко В.И. Ветошников М.О. Проверила: Харисова Э.А. Уфа 2019 Задание для самостоятельного выполнения 1) Разбейте множество объектов из набора данных pluton на 3 кластера методом центров тяжести (kmeans). Сравните качество разбиения в зависимости от макисмального числа итераций алгоритма. 2) Сгенерируйте набор данных в двумерном пространстве, состоящий из 3 кластеров, каждый из которых сильно «вытянут» вдоль одной из осей. Исследуйте качество кластеризации методом clara в зависимости от 1)использования стандартизации; 2)типа метрики. Объясните полученные результаты. 3) Постройте дендрограмму для набора данных votes.repub (число голосов, поданных за республиканцев на выборах с 1856 по 1976 год). Проинтерпретируйте полученный результат. Выполнение задания:
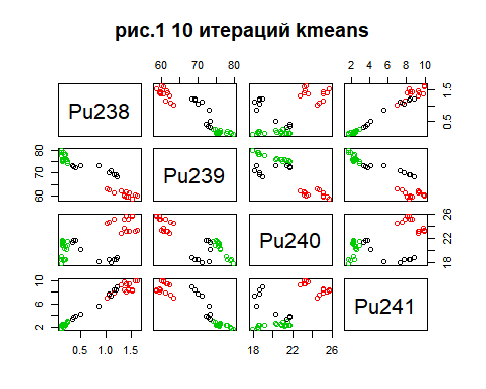
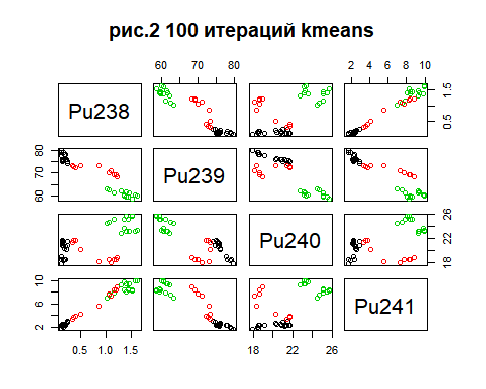
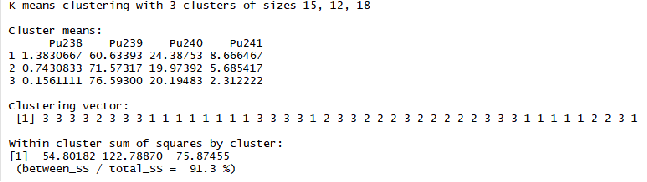
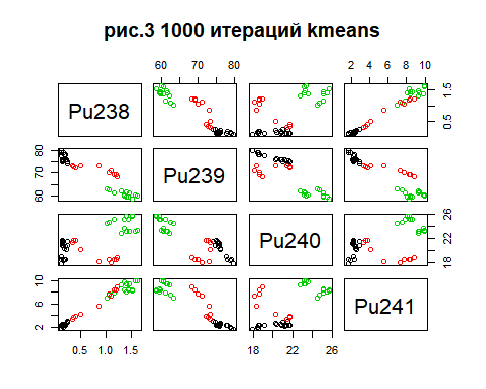
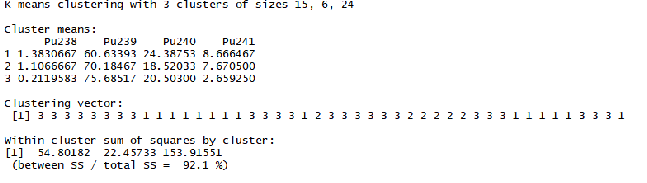
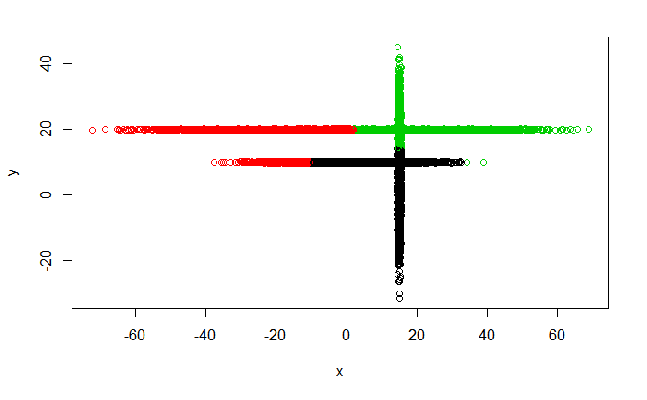
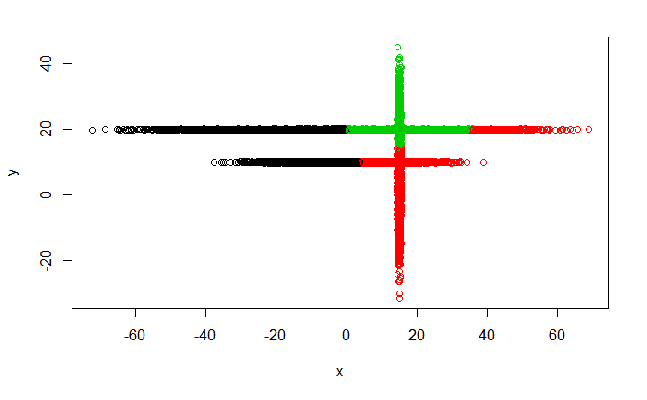
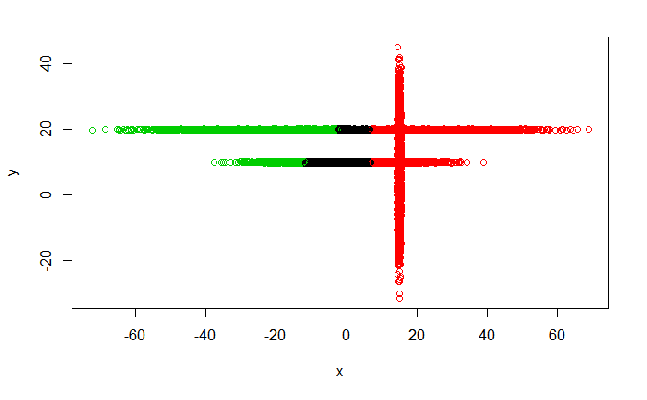
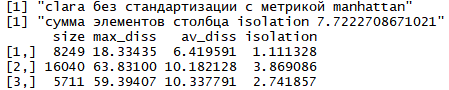
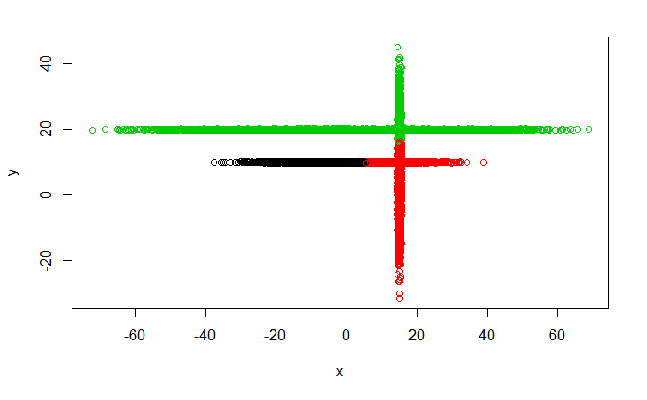
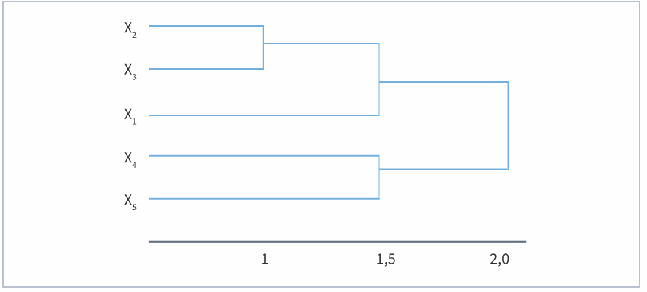
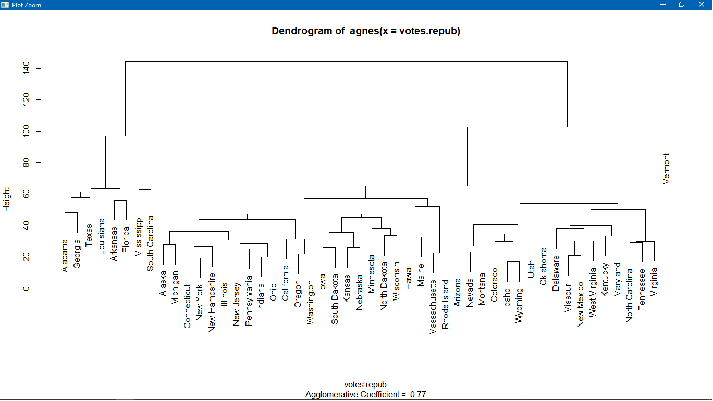
Метод k-средних (англ. k-means) — наиболее популярный метод кластеризации. Был изобретён в 1950-х годах математиком Гуго Штейнгаузом и почти одновременно Стюартом Ллойдом. Особую популярность приобрёл после работы Маккуина. Действие алгоритма таково, что он стремится минимизировать суммарное квадратичное отклонение точек кластеров от центров этих кластеров: 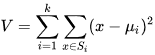 где  — число кластеров,  — полученные кластеры,  , а  — центры масс всех векторов  из кластера .По аналогии с методом главных компонент центры кластеров называются также главными точками, а сам метод называется методом главных точек и включается в общую теорию главных объектов, обеспечивающих наилучшую аппроксимацию данных.  Часть данных датасета Pluton Подключим библиотеку 'cluster' с датасетом pluton (набор данных состоящий из 45 строк и 4 столбца, содержащие проценты изотопного состава 45 плутониевых партий) и запустим алгоритма kmeans c 10,100,1000 максимальными итерациями. Затем выведем получившиеся графики кластеров и посмотрим кол-во фактических итераций, которые понадобились kmeans для кластеризации. library(cluster) #Загрузка библиотеки clusterc датасетом pluton data10 <- kmeans(pluton, 3, iter.max = 10) #Запуск kmeans с 10 итерациями data100 <- kmeans(pluton, 3, iter.max = 100) #Запуск kmeans с 100 итерациями data1000 <- kmeans(pluton, 3, iter.max = 1000) #Запуск kmeans с 1000 итерациями plot(pluton, col = data10$cluster, main = "рис.1 10 итераций kmeans") #Вывод графика результатов kmeans с 10 итерациями plot(pluton, col = data100$cluster, main = "рис.2 100 итераций kmeans")#Вывод графика результатов kmeans с 100 итерациями plot(pluton, col = data100$cluster, main = "рис.3 1000 итераций kmeans")#Вывод графика результатов kmeans с 1000 итерациями paste("Кол-во фактических итераций", data10$iter, "Кол-во максимальных итераций 10") paste("Кол-во фактических итераций", data100$iter, "Кол-во максимальных итераций 100") paste("Кол-во фактических итераций", data1000$iter, "Кол-во максимальных итераций 1000") 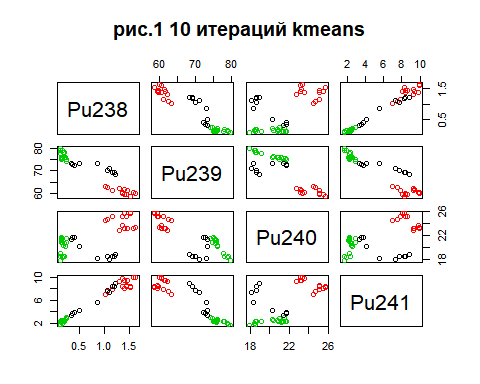 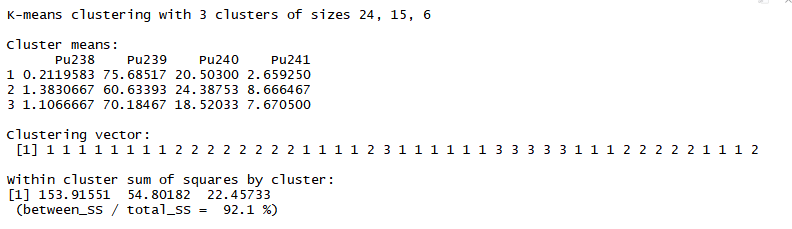 Рисунок 1 – Результаты кластеризации методом центров тяжести при максимальном числе итераций равном 10. Пояснить, что в результате. 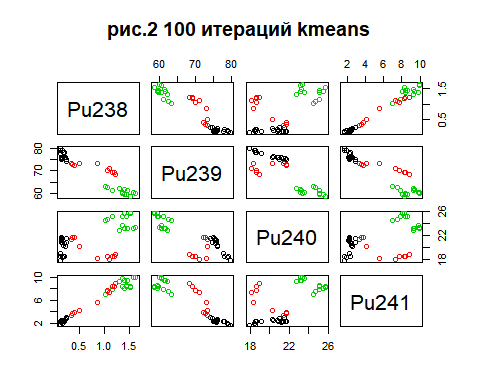 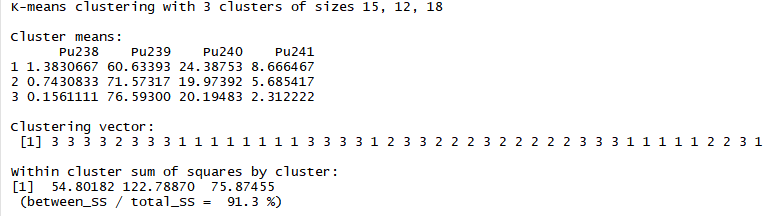 Рисунок 2 – Результаты кластеризации методом центров тяжести при максимальном числе итераций равном 100. 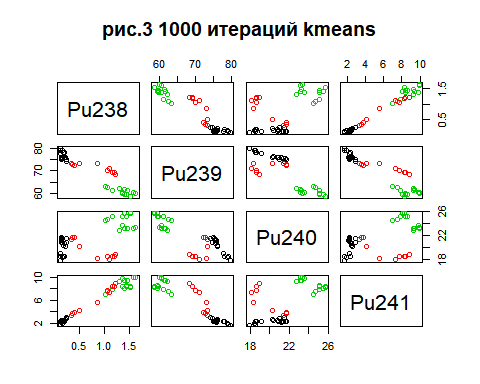 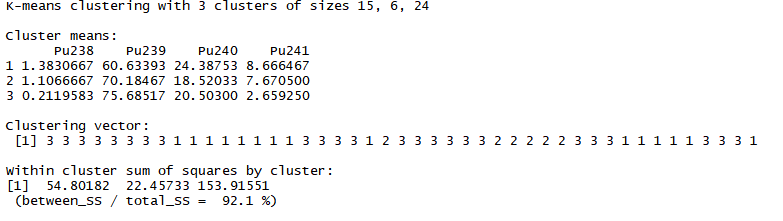 Рисунок 3 – Результаты кластеризации методом центров тяжести при максимальном числе итераций равном 1000. Как видно на графиках, уже при 100 итерациях ничего не изменяется. При заданных 10 максимальных итерациях, kmeans уже завершает свои расчеты.  В выводе мы наблюдаем подтверждение наших предположений. Уже при 10, 100, 1000 заданных нами итераций, kmeans потребовалось всего лишь 2 итерации. Значит и 10 итераций будет много для таких данных, поскольку, фактически, kmeans сделал всего 2 итерации. Так же отношение межкластерной дисперсии к внутрикластерной равно 92,1 %, что является хорошим показателем, означающим что объекты, входящие в один и тот же кластер, были расположены в пространстве переменных близко, а входящие в разные кластеры - далеко друг от друга. Сlustering vector показывает, к какому классу был отнесен каждый элемент. А средние значения в каждом кластере для каждого столбца данных представлено в разделе Cluster Means. 2) Сгенерируйте набор данных в двумерном пространстве, состоящий из 3 кластеров, каждый из которых сильно «вытянут» вдоль одной из осей. Исследуйте качество кластеризации методом clara в зависимости от 1)использования стандартизации; 2)типа метрики. Объясните полученные результаты. Следующий шаг к улучшению масштабируемости k-medoids — это довольно известная модификация PAM, называемая CLARA. Из исходного графа случайным образом выбирается подмножество вершин, и кластеризуется подграф, образованный этими вершинами. Затем (в предположении связности графа) оставшиеся вершины просто распределяются по ближайшим медоидам из подграфа. Вся соль clara состоит в последовательном прогоне алгоритма на разных подмножествах вершин и выборе наиболее оптимального из результатов. Выбор объёма подвыборки для CLARA также представляет собой компромисс между качеством и скоростью. Чем больше кластеров присутствует в данных, тем меньше наши возможности для семплинга: некоторые кластеры могут просто не попасть в выборку. Если разница в размерах кластеров большая, то такой подход вообще противопоказан. По всей видимости, CLARA изначально предназначался для уменьшения времени выполнения алгоритмов кластеризации, чья вычислительная сложность растет быстрее, чем число вершин (когда прогнать несколько раз на подграфе быстрее, чем один раз на полном графе). Поэтому польза CLARA при использовании улучшенной эвристики (линейная сложность) резко падает. В алгоритме CLARA используется стандартизация и метрики расстояния. Представить начальный сгенерированный набор данных Cгенерируем набор данных состоящий из трех кластеров, каждый из которых вытянут вдоль прямой. Исходные данные представляют собой x- случайно сгенерированные нормально распределенные наборы данных состоящий из 10000 элементов каждый со средним значением mean и стандартным отклонением, равным sd. x <- rbind(cbind(rnorm(10000, mean = 0, sd = 10), rnorm(10000, mean = 10, sd = 0.1)),cbind(rnorm(10000,mean = 0,sd = 20),rnorm(10000, mean = 20, sd = 0.1)), cbind(rnorm(10000, mean = 15, sd = 0.2), rnorm(10000,mean = 8, sd = 10))) Метрики расстояния: Сходство или различие между объектами классификации устанавливается в зависимости от выбранного метрического расстояния между ними. Если каждый объект описывается  свойствами (признаками), то он может быть представлен как точка в -мерном пространстве, и сходство с другими объектами будет определяться как соответствующее расстояние. При классификации используются различные меры расстояния между объектами. 1. Евклидово расстояние Это, пожалуй, наиболее часто используемая мера расстояния. Она является геометрическим расстоянием в многомерном пространстве и вычисляется следующим образом: 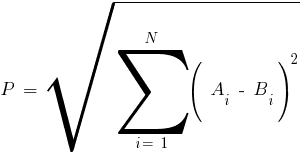 2. Хеммингово расстояние Также называется манхэттенским, сити-блок расстоянием или расстоянием городских кварталов. Это расстояние является разностью по координатам. В большинстве случаев эта мера расстояния приводит к таким же результатам, как и для обычного расстояния Евклида. Однако отметим, что для этой меры влияние отдельных больших разностей (выбросов) уменьшается (так как они не возводятся в квадрат). Хеммингово расстояние вычисляется по формуле:  .Стандартизация: Стандартизация(standardization) или нормирование (normalization) приводит значения всех преобразованных переменных к единому диапазону значений путем выражения через отношение этих значений к некой величине, отражающей определенные свойства конкретного признака. Чтобы проследить зависимость качества кластеризации методом clara от метрики и наличия стандартизации будем использовать в объекте clusinfo, возвращаемым алгоритмом CLARA, cумму элементов столбца isolation (максимальное различие между наблюдениями в кластере и медоидом скопления, поделенное на минимальное различие между медоидом скопления и медоидом любого другого скопления. Если это соотношение мало, кластер хорошо отделен от других кластеров). x <- rbind(cbind(rnorm(10000,0,10),rnorm(10000,10,0.1)),cbind(rnorm(10000,0,20),rnorm(10000,20,0.1)), cbind(rnorm(10000,15,0.2), rnorm(10000,8,10))) clarax <- clara(x, 3, stand=TRUE, metric = "euclidean") #clara со стандартизацией с метрикой "euclidean" print(sum(clarax$clusinfo[,4])) print(clarax$clusinfo) plot(x,col=clarax$clustering, xlab="x", ylab="y") #отрисовка для clara со стандартизацией с метрикой "euclidean" clarax <- clara(x,3, stand=FALSE, metric = "euclidean") #clara без стандартизации с метрикой "euclidean" print(sum(clarax$clusinfo[,4])) print(clarax$clusinfo) plot(x,col=clarax$clustering, xlab="x", ylab="y") #отрисовка для clara без стандартизации с метрикой "euclidean" clarax <- clara(x,3, stand=FALSE, metric = "manhattan") #clara без стандартизации с метрикой "manhattan" print(sum(clarax$clusinfo[,4])) print(clarax$clusinfo) plot(x,col=clarax$clustering, xlab="x", ylab="y") #отрисовка для clara без стандартизации с метрикой "manhattan" clarax <- clara(x,3, stand=TRUE, metric = "manhattan") #clara со стандартизацией с метрикой "manhattan" print(sum(clarax$clusinfo[,4])) print(clarax$clusinfo) plot(x,col=clarax$clustering, xlab="x", ylab="y") #отрисовка для clara со стандартизацией с метрикой "manhattan" 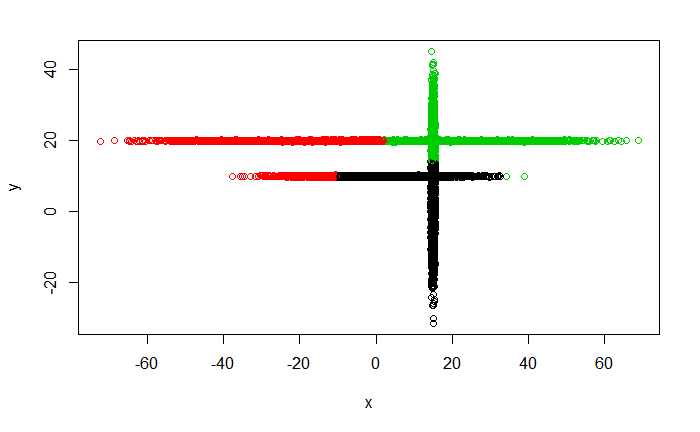 Рисунок 4 - Кластеризация с использованием евклидова расстояния и стандартизацией  Вывести результаты использования всех метрик. Ошибки. На каком основании вы делаете какие-то выводы? 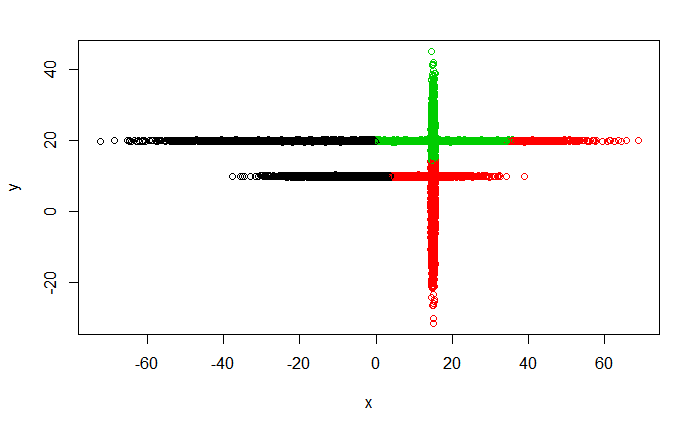 Рисунок 5 - Кластеризация с использованием евклидова расстояния без стандартизации  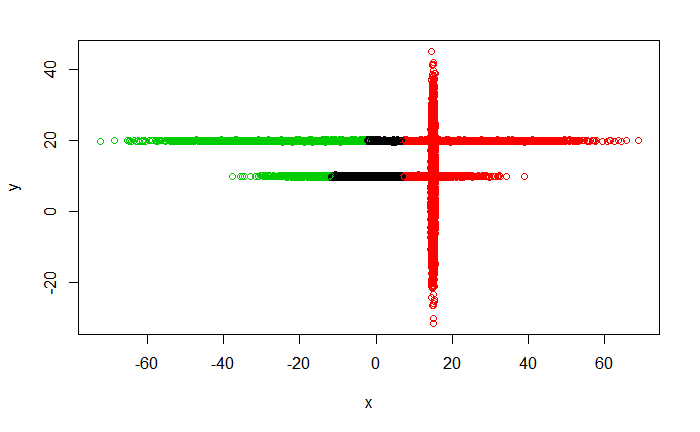 Рисунок 6 - Кластеризация с использованием манхэтонского расстояния и без стандартизации  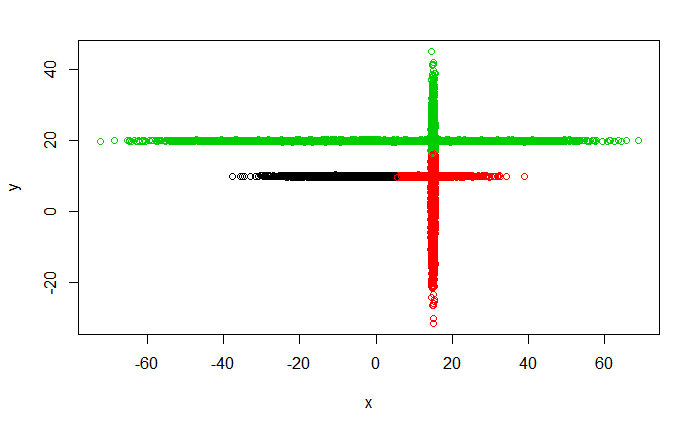 Рисунок 7 - Кластеризация с использованием манхэтонского расстояния и стандартизации  В выводе мы наблюдаем, что самая наименьшая сумма элементов столбца isolation у CLARA с стандартизацией и метрикой manhattan. Исходя из полученных результатов можно сделать вывод, что алгоритм CLARA c стандартизацией и метрикой manhattan самый лучший. 3) Постройте дендрограмму для набора данных votes.repub (число голосов, поданных за республиканцев на выборах с 1856 по 1976 год). Проинтерпретируйте полученный результат. Дендрограмма показывает степень близости отдельных объектов и кластеров, а также наглядно демонстрирует в графическом виде последовательность их объединения или разделения. Количество уровней дендрограммы соответствует числу шагов слияния или разделения кластеров. В нижней части рисунка расположена шкала, на которой откладывается расстояние между объектами в пространстве признаков. 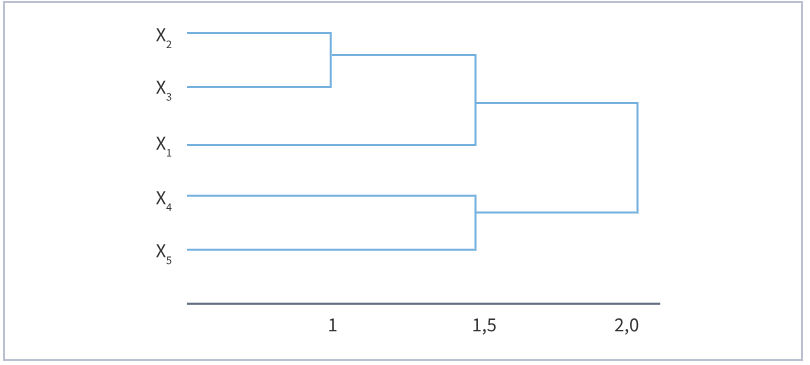 Рисунок 8 – Пример дендрограммы В дендрограмме, представленной на рисунке, на первом шаге группируются объекты x2 и x3, образуя кластер (x2,x3) с минимальным расстоянием (например, Евклидовым) между объектами, примерно равным 1. Затем объекты x4 и x5 и группируются в другой кластер (x4,x5) с расстоянием между ними, равным 1,5. Дистанция между кластерами (x2,x3) и (x1) также оказывается равной 1,5, что позволяет сгруппировать их на том же уровне, что и (x4,x5). И наконец два кластера (x1,x2,x3) и (x4,x5) группируются на самом высоком уровне иерархии кластеров с расстоянием 2. Иерархические агломеративные методы (Agglomerative Nesting, AGNES) Эта группа методов характеризуется последовательным объединением исходных элементов и соответствующим уменьшением числа кластеров. В начале работы алгоритма все объекты являются отдельными кластерами. На первом шаге наиболее похожие объекты объединяются в кластер. На последующих шагах объединение продолжается до тех пор, пока все объекты не будут составлять один кластер. Построим дендрограмму голосов республиканцев полученных в разных городах в разные года и выведем ее. plot(agnes(votes.repub)) #Построение и вывод дендрограммы голосов республиканцев 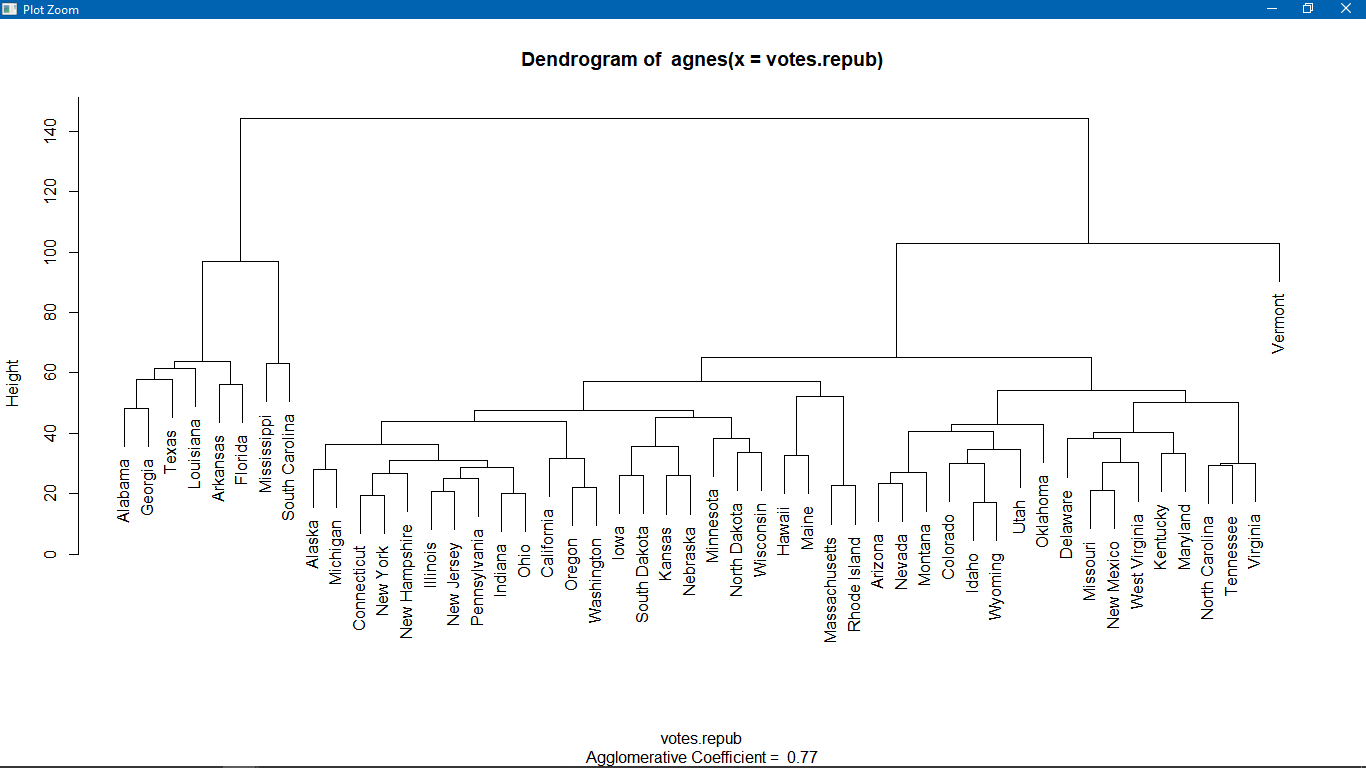 Рисунок 9 – Дендрограмма кластеризации голосов республиканцев На дендрограмме разделения данных по количеству голосов, отданных за республиканцев мы можем наблюдать что наши данные разбились на два кластера. Каждый из двух больших кластеров разделен на подкластеры. На дендрограмме по вертикали отображается расстояние (или иная мера сходства), при котором произошло объединение. Расстояние влияет на объединение в кластеры. К первому кластеру относятся штаты, в которых республиканцы практически не одерживали побед на выборах в период с 1856 по 1976(Alabama, Georgia, Texas, Louisiana, Arkansas, Florida, Mississippi, South Carolina). Ко второму кластеру отнесены штаты, в которых граждане чаще отдавали предпочтение республиканцам на выборах Alaska, Michigan, Connecticut, New York, New Hampshire, Illinois, New Jersey, Pennsylvania, Indiana, California, Oregon, Washington DC, Iowa, South Dakota, Wisconsin, Hawaii, Maine, Massachusetts, Rhode Island, Arizona,Nevada,Montana,Colorado,Idaho,Wyoming,Utah,Oklahoma,Delaware,Missouri,New Mexico,West Virginia,Kentucky,Mary Land,North Carolina,Tennessee,Virginia,Vermont. Чем правее расположен подкластер, тем более выражено преимущество республиканцев над демократами в штатах, входящих в данный подкластер. Таким образом в период с 1856 по 1976 самым демократичным штатом оказалась Алабама, а самым республиканским – Вермонт. В этом легко убедиться если рассмотреть сколько раз республиканцы одерживали победу в период с 1856 по 1964 в любом штате из первого кластера и второго кластера. Например, в Алабаме республиканцы выиграли всего несколько количество раз.  Рисунок 10 – Распределение голосов в штате Алабама Во втором кластере, напротив находятся штаты где победу чаще одерживали республиканцы. Например, в Вермонте демократы победили всего 1 раз.  Рисунок 11 – Распределение голосов в штате Вермонт |