Отчет о лабораторной работе № 1 (вариант №3). 1 лабораторная. Отчет о лабораторной работе 1 (вариант 3) Разветвляющийся вычислительный процесс по дисциплине Программирование
 Скачать 104.76 Kb. Скачать 104.76 Kb.
|
|
Министерство науки и высшего образования РФ Федеральное государственное бюджетное образовательное учреждение высшего образования ИРКУТСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Институт информационных технологий и анализа данных Отчет о лабораторной работе № 1 (вариант №3) «Разветвляющийся вычислительный процесс» по дисциплине «Программирование»
Иркутск 2022 Условие задачи Даны действительные числа Х, Y. Если оба числа отрицательны, то каждое число заменить его модулем; если отрицательное только одно из них, то оба значения увеличить на 0.5; если оба числа положительны и ни одно из них не принадлежит отрезку [ 0.5, 2.0 ], то оба значения уменьшить в 10 раз; в остальных случаях числа оставить без изменения. Введем следующие обозначения: 1var – первое условие с 2 отрицательными числами; 2var – второе условие с одним отрицательным числом; 3var – третье условие с 2 положительными числами не принадлежащий отрезку; 4var – остальные случаи; Таблица 1 – Внешние спецификации
Алгоритмизация Блок-схема представлена на рис 1. 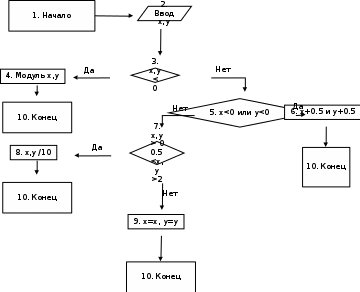 Рисунок 1. Проектирование тестов Таблица 2 – таблица тестов
Тест 1: блоки 1,2,3,4; Тест 2: блоки 1,2,3,5,6; Тест 3: блоки 1,2,3,5,7,8; Тест 4: блоки 1,2,3,5,7,9; Кодирование алгоритма или запись алгоритма на языке С++ #include"math.h" #include using namespace std; int main() { float x, y; cout << "Введите число x: "; cin >> x; cout << "Введите число y: "; cin >> y; if (x < 0 && y < 0) { x = fabs(x); y = fabs(y); } else if (x < 0 || y < 0) { x = x + 0.5; y = y + 0.5; } else if ((x > 0 && y > 0) && (x < 0.5 || x > 2.0) && (y < 0.5 || y > 2.0)) { x = x / 10; y = y / 10; } cout << "x = " << x << endl; cout << "y = " << y << endl; return 0; } Условие задачи Заданы действительные числа X и Y. Определить, принадлежит ли точка с координатами (X,Y) заштрихованной части плоскости.(см. рис. 2). 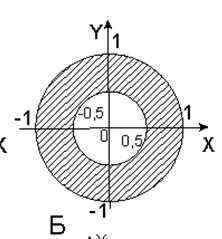 Рис. 2 Математическая модель Для определения заштрихованной области используем формулу окружности x^2+y^2=R^2. Так мы сможем создать условие нахождения заштрихованной области между двумя окружностями. Таблица 1 – Внешние спецификации
Таблица сообщений: С1: «Точка принадлежит заштрихованной части плоскости.» С2: «Точка не принадлежит заштрихованной части плоскости.» Алгоритмизация 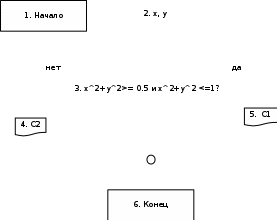 Рисунок 1 – Блок-схема алгоритма Проектирование тестов
Проверка правильности алгоритма с помощью таблицы: Тест 1: блоки 1,2,3,5,6 Тест 2: блоки 1,2,3,4,6 Кодирование алгоритма или запись алгоритма на языке С++ #include #include using namespace std; int main() { float x,y; cout << "Введите координату x: "; cin >> x; cout << "Введите координату y: "; cin >> y; if (((x*x+y*y) >= 0.5) && ((x*x+y*y) <= 1)) { cout << "Точка принадлежит заштрихованной части плоскости" << endl; } else { cout << "Точка не принадлежит заштрихованной части плоскости" << endl; } return 0; } Условие задачи: Пусть D - заштрихованная часть плоскости (см. рис. 3) и пусть задана точка своими координатами (X,Y). Запись (X,Y) D означает, что точка с координатами X, Y лежит внутри заштрихованной области D. Определить значение функции U следующим образом: 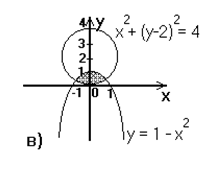  Математическая модель: Используем уравнение окружности x^2+(y-2)^2=4 и уравнение параболы y=1-x^2. Таблица 1 – Внешние спецификации
Алгоритмизация 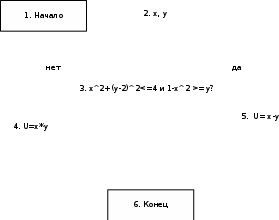 Проектирование тестов
Проверка правильности алгоритма с помощью таблицы Тест1: блоки 1,2,3,5,6 Тест2: блоки 1,2,3,4,6 Кодирование алгоритма или запись алгоритма на языке С++ #include #include using namespace std; int main() { float x,y,u; cout << "Введите координату x: "; cin >> x; cout << "Введите координату y: "; cin >> y; if ((pow(x,2)+pow(y-2,2) <= 4) && (1-pow(x,2) >= y) ) { u = x-y; cout << "U = " << u << endl; } else { u = x*y; cout << "U = " << u << endl; } return 0; } |
