отчет 2. Отчет о практической работе Расчет показателей надежности по эмпирическим данным при малой выборке

• Название: Отчет о практической работе Расчет показателей надежности по эмпирическим данным при малой выборке
• Анкор: отчет 2
• Дата: 22.01.2023
• Размер: 103 Kb.
• Имя файла: Otchet PR 2 - OTN - BMR-19 Familia.doc
• Тип: Отчет; #897951

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Уфимский государственный нефтяной технический университет»

Кафедра «Технологические машины и оборудование»

Отчет

о практической работе

«Расчет показателей надежности

по эмпирическим данным при малой выборке»

Студент гр. БНН 19-01 А.А. Петров
Доцент А.Х. Габбасова


Уфа 2020

Цель. Для возможности прогнозирования надежности объекта выбрать закон распределения при заданных значениях наработки до отказа ряда аналогичных объектов.
Задание

Выявить закон распределения, который отражает с высокой степенью достоверности реальную картину потери надежности объекта, работающего на нефтеперерабатывающем предприятии. Статистическая проработка позволила установить наработки до отказов ряда аналогичных объектов, ч:

Номер варианта	Наработка до отказа аналогичных объектов, ч
33	123, 218, 230, 210, 234, 217, 200, 157

Оценить параметры закона распределения.

Решение
1) Определяем к какому типу относится статистическая выборка (малая или большая). Количество испытанных объектов (объем выборки) N = 8 < 20 – малая выборка.

2) Строим вариационный ряд наработки

t₁ < t₂ < t₃ < t₄ < … < t_n, (1)

где t_i - наработка до отказа i – го объекта, ч.

123 157 200 210 217 218 230 234

3) Для каждого значения определяем показатели надежности P_i(t), F_i(t), _i(t). Результаты сводятся в таблицу 1.

В таблице 1 оценка вероятности безотказной работы в i-й по порядку момент времени t_i определяется:

P(t_i)= , (2)

где i – номер по порядку в вариационном ряду.

Оценка вероятности безотказной работы в первый по порядку момент времени t₁:

P(123)=

Вероятность отказа в i-й по порядку момент появления отказа t_i оценивается как:

, или F(t_i)=1 - P(t_i). (3)

Вероятность отказа в первый по порядку момент появления отказа t₁:

F(123)=1 - P(123) = 1 - 0,917 = 0,083.

Интенсивность отказов в i-й по порядку момент времени t_i определяется следующим образом:

, (4)

где t_i+1 – наработка до отказа в следующий по порядку момент времени.

Интенсивность отказов в первый по порядку момент времени t₁=123 ч:

=
Таблица 1 – Результаты расчетов показателей надежности

Номер по порядку	1	2	3	4	5	6	7	8
ti, ч	123	157	200	210	217	218	230	234
Pi(t)	0,917	0,798	0,680	0,560	0,440	0,320	0,202	0,083
F(t)	0,083	0,202	0,320	0,440	0,560	0,680	0,798	0,917
i(t)	0,0038	0,0035	0,0175	0,0310	0,2730	0,0310	0,1470	-

4) Строим гистограммы P_i(t), F(t) и график изменения _i(t) во времени (рисунок 1).

По виду графика изменения _i(t) во времени высказываем гипотезу о законе распределения.

Поскольку график изменения _i(t) во времени имеет минимум и максимум в середине интервала (рисунок 1), то предполагаем, что имеет место нормальный закон распределения случайных величин наработок до отказа.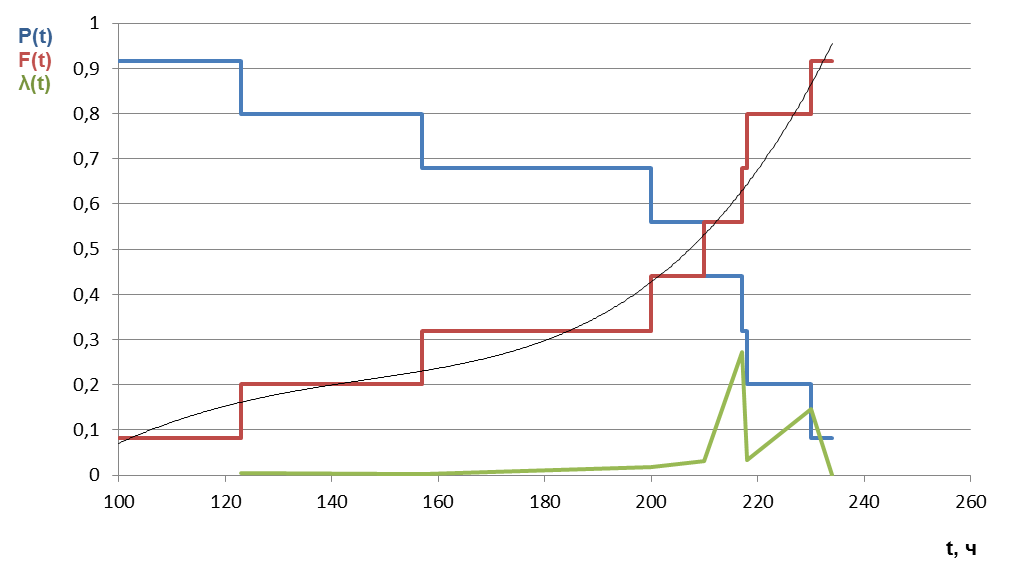

Р(t)

F(t)

F_(t)

D_max

Рисунок 1 - Гистограммы P_i(t), F_i(t) и график изменения _i(t) во времени
5) Оценка параметров предполагаемого закона распределения

Среднее арифметическое значение случайной величины

. (5)

.

Среднее квадратическое отклонение случайной величины: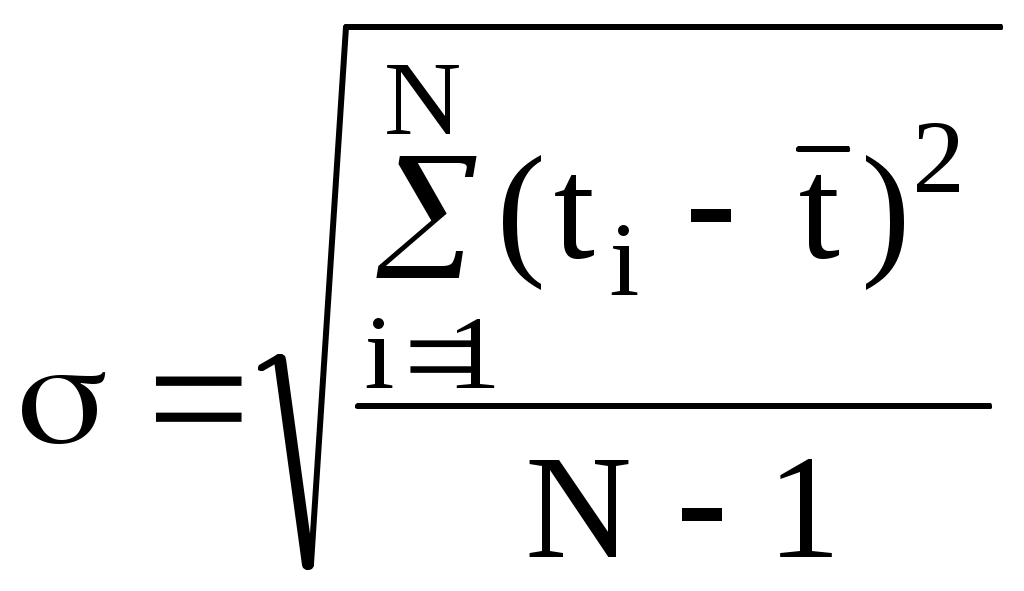

. (6)

.

Коэффициент вариации

. (7)


6) Проверка гипотезы о предполагаемом законе распределения по критерию Колмогорова

Строим теоретическую функцию распределения значения вероятности отказа F*(t) – выравнивающую сглаживающую кривую изменения вероятности отказа во времени (см. рисунок 1) – линию тренда в Excel (рекомендуется полиномиальная линия тренда). Построить либо в Excel, либо на миллиметровой бумаге – оси обозначить, единицы измерения указать!!!

Критерий Колмогорова определяется из графиков как наибольшее абсолютное отклонение между статистической F(t) и теоретической F*(t) функциями вероятностей отказов (см. рисунок 1). На рисунке D_max показать:

D_max=max |F*(t) - F(t)|. (8)

D_max= max |F*(t) - F(t)|=0,17.

Определяем условную интенсивность:

.



Далее по справочным данным (приложение А) по значению * определяется условная вероятность Р(*).

Если вероятность Р(*) не является малой ( 0,5), то гипотеза о предполагаемом законе распределения не противоречит опытным данным.

Итак,

Р(*) = Р(0,5) = 0,964 > 0,5.
Вывод

Поскольку условная вероятность Р(*) > 0,5, то гипотеза о предполагаемом законе распределения не противоречит опытным данным. Для возможности прогнозирования надежности объекта принимаем нормальный закон распределения случайных величин.