Отчет о работе выполняется в виде пояснительной записки. В отчет включаются следующие разделы задание, технические условия, постановка задачи, математическое обеспечение (математические методы и алгоритмы),

• Название: Отчет о работе выполняется в виде пояснительной записки. В отчет включаются следующие разделы задание, технические условия, постановка задачи, математическое обеспечение (математические методы и алгоритмы),
• Дата: 30.06.2022
• Размер: 172.88 Kb.
• Имя файла: kr-1ch.docx
• Тип: Отчет; #621701

Введение

 

Для выполнения контрольной работы требуется изучить теоретический материал и разработать программу в соответствии с Вашим вариантом. Номер варианта соответствует порядковому номеру студента в журнале учебной группы.

Отчет о работе выполняется в виде пояснительной записки. В отчет включаются следующие разделы – задание, технические условия, постановка задачи, математическое обеспечение (математические методы и алгоритмы), программная реализация, экспериментальная часть, заключение, список литературных источников, приложения.

Защита проводится либо в форме видеоконференции, либо в виде тестовых вопросов с ограничением времени на подготовку ответа.

1. Структуры данных

Данные – набор знаков, которые изображают некоторую информацию, которую можно извлечь, если известен смысл, приписываемый данным.

В общем случае ЭВМ выполняет обработку данных или, другими словами, информации.

Строка – упорядоченный набор элементов, каждый из которых, кроме первого, имеет предшественника и, кроме последнего, последователя.

Получить доступ к элементам строки можно только путем последовательного просмотра элементов с одного из концов строки. Входной структурой данных для транслятора является строка.

Массив – набор элементов, с каждым из которых связан кортеж (вектор) целых чисел, компоненты которого называются индексами.

Очереди и стеки – одномерные динамически изменяемые упорядоченные наборы элементов, новый элемент добавляется всегда к одному и тому же концу.

Элемент из очереди извлекается с противоположного конца, т. е. – по принципу FIFO. Элемент из стека удаляется с того же конца, куда производится добавление, т. е. по принципу LIFO. Для стека существует понятие вершины. Очереди, как правило, оформляются в виде циклической структуры и используются для реализации буферов. Стеки используются в синтаксических распознавателях и в семантических программах, осуществляющих генерацию объектного кода.

Таблица – набор элементов, каждый из которых имеет отличительный признак, называемый ключом.

Поиск в таблице производится по ключу. Кроме ключа элемент таблицы содержит специфичные данные, содержащие определённую информацию, например, в компиляторах используются таблицы символических имён. Ключом в этой таблице является идентификатор.

Таблица 1 – Таблица и ее элементы
Ключ	Данные
	тип	адрес	значение
R12	float	6000 0102	5.3
j	int	4000 0200	0

Двоичное дерево – элемент, который состоит из набора узлов (вершин), каждый из которых помимо данных содержит два указателя.

Единственный узел самого верхнего уровня называется корнем, а узлы самого нижнего уровня называются листьями. В дереве существует лишь один путь от корня к конкретному узлу. При помощи деревьев представляются иерархические отношения между данными. Например, для оператора присваивания y=a+b*c можно представить порядок вычисления с помощью дерева: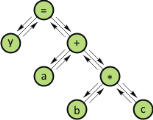

Рисунок 1 – Двоичное дерево

Ориентированный граф отличается от дерева тем, что на узел может указывать более чем один указатель. Для отличия указывающих узлов от указываемых на графе ставятся стрелки. В ориентированном графе возможен путь из узла к самому себе.

Используются ориентированные графы для описания схем алгоритмов.

2. Хранение структурированных данных

 

Структурированные данные хранятся в памяти ЭВМ в виде различных структур хранения. Набор структур хранения ограничен, так как память ЭВМ представляет собой упорядоченную последовательность непосредственно адресуемых байтов. Структуры хранения состоят из элементов. Элемент может образовываться из нескольких байт и наоборот, в одном байте может быть размещено несколько элементов. Типичными структурами хранения являются вектор, список и сеть.

Вектор – набор элементов хранения одинакового размера, которые располагаются в памяти последовательно.

Вектор определяется базой, которая является адресом первого элемента вектора. Кроме этого, в определение вектора входят размер элемента и их количество. Если элементы вектора имеют одинаковые размеры, то доступ к i-тому элементу вектора можно осуществлять с помощью выражения:

l(i-1),

где l – длина элемента.

Список – набор элементов, каждый из которых состоит из двух полей: данные и указатель.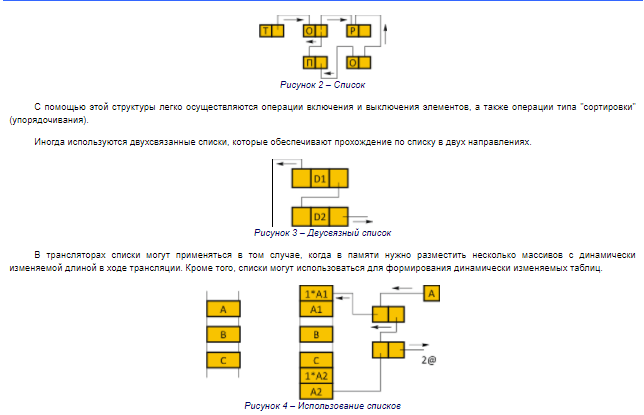

Для массива А есть элемент продолжения, то есть элемент списка, который содержит указатель на начало массива. В начале каждого элемента массива может стоять длина. Эта длина используется для поиска.

Сети – структуры, состоящие из элементов, каждый из которых содержит поле данных и два поля указателей.

Используются сети для представления бинарных деревьев.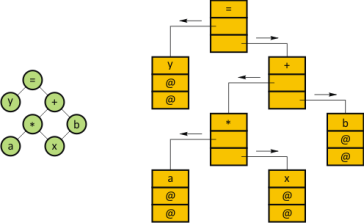

Рисунок 5 – Сеть для представления бинарного дерева выражения y=ах+b

3. Cоответствие структур данных и способов их хранения

3.1. Строки

Строки элементов одинакового размера хранятся в виде векторов. Строки с элементами большой длины хранятся в виде списков. Хранение в виде списков используются в том случае, когда требуется выполнение над строками специальных операций: конкатенация, выделение хвоста (Tail), выделение головы (Head) и тому подобное.

3.2. Массивы

Как правило хранятся в виде одномерного вектора. Это связано с тем, что при таком способе хранения формализуются способы поиска элементов массива. Различают хранение одномерных массивов:

• 
  по столбцам (1);
  
• 
  по строкам (2).
  

где:

• 
  при отображении строками:
  

D_n = 1; D_m = (k_m+1 – i_m+1+1) D_m+1, m = n-1, n-2, …1;

• 
  при отображении столбцами:
  

D₁ = 1; D_m = (k_m-1 – i_m-1+1) D_m-1, m = 2, 3, … n.

Если вектор T имеет базу b, то формула для нахождения адреса b в векторе t представляется в таком виде:



3.3. Контрольные вопросы

Для студентов предлагаются следующие контрольные вопросы:

1. 
   приведите вывод формулы индекса вектора отображения для индексированной переменной многомерного массива размещенного по столбцам;
   
2. 
   приведите вывод формулы индекса вектора отображения для индексированной переменной многомерного массива размещенного по столбцам;
   
3. 
   объявите на языке С++ обобщенный стек;
   
4. 
   объявите на языке С++ обобщенную очередь;
   
5. 
   объявите на языке С++ обобщенное бинарное дерево;
   
6. 
   объявите на языке С++ обобщенный список.
   

4. Организация таблиц

4.1. Общие положения

Таблицы являются одной из наиболее употребляемых структур данных, используемых в трансляторах. В таблицах хранят основные символы входного языка, которые используются для распознавания синтаксических конструкций и коды операций объектного языка, необходимые для генерирования объектного кода.

Указанные типы таблиц указываются заранее и являются постоянными.

Кроме постоянных таблиц в ходе работы транслятора вырабатываются временные таблицы. К временным таблицам относятся:

1. 
   таблица символических имен (идентификаторы);
   
2. 
   таблица литералов (константы).
   

Основной характеристикой способа организации таблиц является время поиска одной записи. Это время пропорционально средней длине поиска, под которой понимается среднее количество записей, просматриваемых для отыскания требуемой записи.

4.3. Древовидные таблицы

Иногда в качестве временных таблиц используются древовидные таблицы, которые представляются в виде бинарного дерева, отображенного в памяти ЭВМ сетью. Каждая запись в такой таблице сопровождается двумя указателями. Первый указатель содержит адрес хранения записи с меньшим указателем ключа, а второй – с большим.

Новые записи добавляются в таблицу подряд. После добавления в таблицу новой записи значение ее ключа сравниваются со значением ключа первой записи. По результату сравнения с помощью указателя определяется адрес сравнения следующей записи, с ключом которой необходимо сравнивать добавляемую запись. Это продолжается до тех пор, пока не будет найдена запись с пустым указателем. В этот указатель нужного направления записывается адрес хранения добавляемой записи.

Пример:

Пусть поступают записи, имеющие значения ключей соответственно 6, 3, 5, 7, 1.

Дерево будет иметь вид, представленный на рисунке.

Рисунок 6 – Дерево для последовательности ключей – 6, 3, 5, 7, 1

Записи в таблице будут расположены в соответствии с приведенным для примера деревом.

Таблица 2 – Последовательность ключей
200	6		6				6						6								6
201	@	@		202		@			202			@				202				206					202					206
202			3				3						3								3
203			@		@			@			204				@				204					208					204
204							5						5								5
205							@			@				@				@					@					@
206													7								7
207													@				@					@					@
208																					1
209																					@					@

Поиск в древовидной таблице осуществляется путем сравнения искомого ключа с ключом первой записи. В результате определяется адрес (направление) следующего ключа для сравнения и так далее. Например, поиск ключа 5 имеет вид:

[200]→6→[202]→3→[204]→5 = 5.

Средняя длина поиска зависит от порядка поступления записей. В худшем случае, когда записи поступают в порядке возрастания ключа (или убывания), дерево будет иметь одну единственную ветвь и длина поиска приблизительно будет равна n/2.

Для сбалансированных деревьев, которые имеют вид: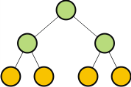

Рисунок 7 – Сбалансированное дерево

Средняя длина поиска вычисляется по формуле:

D₂ = log₂(n+2).

Это следует из того, что в сбалансированном двоичном дереве число ветвей n связано с числом уровней дерева Х соотношением:

2^Х-2 = n.

В общем случае (когда несбалансированное дерево) применяют формулу:

D₂=sqrt(n/2·D₂).

Недостаток данных таблиц – избыточное количество памяти по сравнению с неупорядоченными.

Кроме древовидных таблиц применяются упорядоченные таблицы, где упорядоченными могут быть по принципу возрастания (убывания) ключа либо по принципу наиболее высокой частоты обращения записи.

Упорядочивание может производиться различными методами. Наиболее простыми являются метод пузырька и метод перестановок.

4.4. Таблицы с вычисляемыми входами

Если в таблице из m записей все записи имеют разные значения ключа: k₁, …, k_m, и таблица отображается на вектор A[1…n], причём m<n, а также определена функция f(k_j) такая, что для любого k_j j меняется от 1 до m, а f(k_j) принимает значения от 1 до n целого типа, и f(k_j) <> f(k_j) при i<>j и при i, j, изменяющихся от 1 до m. В этом случае табличная запись с ключом k однозначно отображается в элемент вектора A[f(k)]. Следует отметить, что это отображение является взаимно однозначным.

Таким образом определяемая функция f(k) называется функцией расстановки или ХЕШ-функцией. Подбор функции расстановки, обеспечивающей взаимно однозначное отображение, применяется лишь для постоянных таблиц. Для таблиц временного значения, динамически изменяющихся, от требований взаимной однозначности отказываются.

Длина доступа в ХЕШ таблице D₃=1.

Учитывая то, что взаимную однозначность преобразования ключа в номер записи, в общем случае достичь практически невозможно, от этого требования отказываются, и в этом случае на одну позицию таблицы претендует некоторое множество ключей. В этом случае функцию расстановки подбирают из условия наиболее равномерного распределения отображения ключей в номера строк. Таблицы, построенные по такому принципу, называются таблицами со случайными перемешиванием. Случайное перемешивание не устраняет наложения записи одной на другую, поэтому нужно принимать дополнительные меры. Такое наложение записей называется коллизией.

Известны два метода решения задач о коллизии:

• 
  1-й метод - рехеширование;
  
• 
  2-й метод - метод цепочек переполнения.
  

Рехеширование

ХЕШ-функция возвращает индекс h. Пусть при хешировании символа s обнаруживается, что соответствующая позиция занята, тогда проверяется элемент таблицы с адресом:

(h+p₁)_modN,

где N – длина таблицы.

Если обнаруживается, что и этот элемент занят, то вычисляется следующий индекс (h+p₂)_modN и т.д. Если обнаруживается ситуация, что p_i=0, то таблица занята.

Для вычисления p_i используют разные методы:

1. 
   Линейное рехеширование.
   

Алгоритм линейного рехеширования:

• 
  Вычислить j=i=f(s).
  
• 
  Если при включении новой записи в таблицу позиция свободна, а при выборке содержит искомый ключ s, то поиск завершен, в противном случае - пункт 3).
  
• 
  Положить i=(i+1)_modN. Если i<>j, то пункт 2), иначе пункт 4).
  
• 
  Ошибка.
  

Пример

В таблице имен, имеющей 8 позиций, требуется разместить идентификаторы a, c1, a3, b1, a4, h, h1. Пусть идентификатор начинается с одной из 8-и букв от а до h, а значение функции расстановки равняется порядковому номеру в алфавите 1-ой буквы идентификатора.

Рисунок 8 – Таблица с линейным рехешированием

При линейном рехешировании возникает проблема скопления элементов, поэтому иногда применяют случайное рехеширование. В этом методе p_i вычисляется случайным образом, и если длина таблицы N=2^k, то можно использовать в качестве p_i случайное двоичное число, состоящее из k разрядов.

2. 
   Рехеширование сложением.
   

Здесь используется формула p_i=i·h, где h-исходный ХЕШ-индекс, т.е. проверяются h, 2h, 3h, … Этот метод можно использовать только тогда,когда N – простое число.

3. 
   Квадратичное рехеширование.
   

В этом случае:

p_i = a_i²+b_i+c,

где N – простое число;

коэффициенты a, b, c – произвольные числа, которые выбираются из определенных условий.

Этот метод ослабляет проблему скопления.

Устранение коллизий методом цепочек переполнения

Для записи цепочек переполнения в создают дополнительную таблицу. В дополнительной таблице записи переполнения связываются в цепочку. В этом случае таблица будет иметь вид, показанный на рисунке.

Пусть последовательность поступающих на вход идентификаторов имеет вид:

а, с1, а3, b1, a4, h, h1.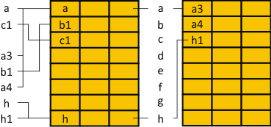

Рисунок 9 – Таблица с цепочками переполнения

Используется также этот метод с внутренними цепочками, при этом заполнение позиций отображающего вектора состоит из двух этапов: используется дополнительная таблица переполнения, а после формирования основной и дополнительной таблиц производится перенесение записи из дополнительной таблицы в основную.

Рисунок 10 – Таблица с внутренними цепочками переполнения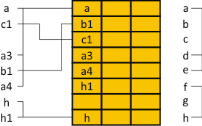

4.5. Контрольные вопросы

1. 
   Какие бывают типы упорядоченных таблиц?
   
2. 
   Как вычислить среднюю длину поиска в древовидной таблице?
   
3. 
   Что влияет на использование таблиц с вычисляемыми входами?
   
4. 
   Какие методы используются для преодоления коллизий?
   
5. 
   В чем заключается принцип линейного рехеширования?
   
6. 
   Для чего используются при построении таблиц цепочки переполнения записей?
   

ДАНЗадание:

Таблица 3 – Задания к контрольной работе
№ вар.	Задание	Структура хранения	Тип таблицы	Отчетность
1.	Определить класс «многомерный массив». Хранение по строкам	1
2.	Определить класс «многомерный массив». Хранение по столбцам.	2
3.	Определить класс «таблица»	1	1
4.	Определить класс «таблица»	2	2
5.	Определить класс «таблица»	1	2
6.	Определить класс «таблица»	2	1
7.	Определить класс «Хеш-таблица». Ключ – однолитерный идентификатор с малыми английскими буквами	1	3
8.	Определить класс «Хеш-таблица». Ключ – двулитерный идентификатор с малыми английскими буквами	2	3
9.	Определить класс «Хеш-таблица». Ключ – двулитерный идентификатор с малыми английскими буквами и цифрами	1	3
10.	Определить класс «Хеш-таблица». Ключ – идентификатор с малыми английскими буквами и цифрами	2	4
11.	Определить класс «Хеш-таблица». Ключ – идентификатор с малыми английскими буквами и цифрами	1	5
12.	Определить класс «Хеш-таблица». Ключ – идентификатор с малыми английскими буквами и цифрами	2	6
13.	Определить класс «Хеш-таблица». Ключ – идентификатор с малыми английскими буквами и цифрами	1	7
14.	Определить класс «Хеш-таблица». Ключ – идентификатор с малыми английскими буквами и цифрами	2	8
15.	Определить класс «многомерный массив». Хранение по строкам	3
16.	Определить класс «многомерный массив». Хранение по столбцам.	4
17.	Определить класс «таблица»	3	1
18.	Определить класс «таблица»	4	2
19.	Определить класс «таблица»	3	2
20.	Определить класс «таблица»	4	1
21.	Определить класс «Хеш-таблица». Ключ – однолитерный идентификатор с малыми английскими буквами	3	3
22.	Определить класс «Хеш-таблица». Ключ – двулитерный идентификатор с малыми английскими буквами	4	3
23.	Определить класс «Хеш-таблица». Ключ – двулитерный идентификатор с малыми английскими буквами и цифрами	3	3
24.	Определить класс «Хеш-таблица». Ключ – идентификатор с малыми английскими буквами и цифрами	4	4
25.	Определить класс «Хеш-таблица». Ключ – идентификатор с малыми английскими буквами и цифрами	3	5
26.	Определить класс «Хеш-таблица». Ключ – идентификатор с малыми английскими буквами и цифрами	4	6
27.	Определить класс «Хеш-таблица». Ключ – идентификатор с малыми английскими буквами и цифрами	3	7
28.	Определить класс «Хеш-таблица». Ключ – идентификатор с малыми английскими буквами и цифрами	4	8

Код структуры хранения

1. 
   – вектор;
   
2. 
   – список;
   
3. 
   – множество;
   
4. 
   – бинарное дерево поиска;
   
5. 
   – дерево
   

Код таблицы

1. 
   – неупорядоченная таблица;
   
2. 
   – упорядоченная таблица по ключу;
   
3. 
   – упорядоченная таблица по частоте обращения ;
   
4. 
   – хеш-таблица;
   
5. 
   – хеш-таблица – линейное рехеширование;
   
6. 
   – хеш-таблица – рехеширование сложением;
   
7. 
   – хеш-таблица – квадратичное рехеширование;
   
8. 
   – хеш-таблица – устранение коллизий цепочками переполнения;
   
9. 
   – хеш-таблица – устранение коллизий внутренними цепочками переполнения.