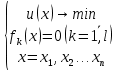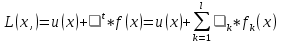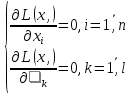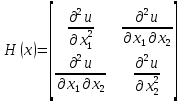Диплом 1 Ракова. Квадратичное программирование
 Скачать 106.64 Kb. Скачать 106.64 Kb.
|
|
МИНОБРНАУКИ РОССИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» Математический факультет Кафедра математического анализа КВАДРАТИЧНОЕ ПРОГРАММИРОВАНИЕ Выпускная квалификационная работа бакалавра 02.03.01 Математика и компьютерные науки Математические методы в экономике и финансах Допущено к защите в ГЭК __.__.20__
Воронеж 20__ СОДЕРЖАНИЕ
ВВЕДЕНИЕ Оптимизационные задачи находят применение в различных сферах и областях науки и являются популярной темой исследования для ученых математиков, экономистов и инженеров всего мира на протяжении последних четырехсот лет. Решать проблемы оптимизации ресурсов посредством использования математических методов как главного инструмента стало возможным в восемнадцатом веке после того, как были впервые представлены работы по методам дифференциального и вариационного исчисления. Особый вклад в развитие данного направления науки был сделан такими учеными, как Лагранж, Фурье, Гаусс и Остроградский. Их труды послужили справочным материалом и для данной работы. Однако наиболее актуальны вопросы оптимизации стали с середины двадцатого века, когда одной из главных макроэкономических задач стало решение проблемы ограниченности ресурсов. Решение задач на нахождение экстремумов функции на множестве ограничений посредством математических методов носит название математического программирования. На сегодняшний день различные типы задач вариационного исчисления называют задачами линейного и нелинейного программирования, и они используются для решения многих экономических проблем, связанных с оптимизацией тех или иных ресурсов, минимизации затрат и максимизации прибыли. К наиболее распространенным примерам подобных задач относятся: задача оптимизации транспортных перевозок (рассматривается проблема ограниченности времени и топлива), задача о наилучшем использования сырья на производстве, задача о составлении оптимального плана работ и рабочих смен и многие другие. Таким образом, задачи оптимизации находят широкое применение в прикладной экономике, а исследование математических методов проблем оптимизации дает возможность составлять и решать задачи самой различной сложности, что обуславливает актуальность и практическую значимость проблематики настоящей работы. Цель работы: Изучить предмет задачи оптимизации и основные методы решения оптимизационных задач квадратичного типа и на основе полученных знаний решить прикладную задачу квадратичного программирования на примере воронежского литейного завода, используя наиболее подходящий под условие задачи метод. Задачи: Исследовать предмет задач квадратичного программирования Исследовать основные методы решения задач квадратичного программирования Рассмотреть примеры решения задач вышерассмотренными методами Составить модель квадратичного типа заданной задачи, используя исходные данные Определить наиболее оптимальные из приведенных методов для решения составленной модели Найти решение данной модели В данной работе рассматриваются различные методы решения оптимизационных задач на примере одного из типов задач нелинейного программирования, а именно квадратичного программирования. В процессе исследования приводятся различные методы решения задач квадратичного программирования. Практический смысл работы: Планируется использовать полученные из решения прикладной задачи данные для применения на ООО «Воронежский литейный завод» с целью оптимизации производства и максимизации прибыли предприятия. Работа выполнена на 42 страницах, содержит 8 рисунков, 13 таблиц, список литературы включает 25 наименований. ТЕОРЕТИЧЕСКИЙ ОБЗОР ПРЕДМЕТА ТЕОРИИ ОПТИМИЗАЦИИ Общая теория оптимизации С развитием математических дисциплин и внедрением их в науки, стало возможно решать задачи с помощью математических методов, что быстро набрало популярность в самых различных сферах. Для того, чтобы приступить к решению подобной задачи, необходимо составить математическую модель. Понятие модели какой-либо задачи, которую предстоит решать математическими методами, представляет собой эквивалент данной проблемы, выраженный на математическом языке. Мы рассматриваем применение методов математики в приложении к задачам, которые связаны с экономическими процессами. Однако данная глава в основном посвящена общей теории задач оптимизации и математического программирования. Задачи оптимизации обыкновенно представляются как математическая модель в виде системы, в которую входят целевая функция и набор ограничений. Задачи математического программирования различаются в зависимости от наличия ограничений, типов переменных, типа целевой функции и некоторых других факторов. Н  езависимо от типа модели, при решении задач математического программирования следует руководствоваться следующим алгоритмом (рис.1.1). езависимо от типа модели, при решении задач математического программирования следует руководствоваться следующим алгоритмом (рис.1.1). Рис. 1.1. Этапы решения задач оптимизации Первым этапом нахождения решения любой задачи оптимизации является определение самой проблемы и формулировка задачи. Далее начинается этап составления модели, доступной для решения задачи с помощью математического программирования. После следует этап выбора наиболее эффективного метода решения составленной модели. Это необходимо, так как для каждого типа моделей оптимизационных задач существуют набор стандартных методов решения. По различным признакам выбирается наиболее эффективный способ решения для каждой конкретной системы. Непосредственное решение задачи выбранным методом (методами) составляет следующий этап, и завершающим этапом становится написание программы для компьютерной реализации. Мы будем анализировать первые четыре этапа решения задачи оптимизации ресурсов на примере воронежского чугунно-литейного завода, опуская этап компьютерной реализации. Общий вид моделей оптимизационных задач представляется следующим образом (1.1):
Целевая функция – это закон, который показывает зависимость рассматриваемых ресурсов, представленных в виде переменных, друг от друга. Решение задачи оптимизации подразумевает поиск максимального (или минимального) значения целевой функции 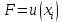 и величин переменных и величин переменных 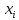 , при которых было получено соответствующее значение. , при которых было получено соответствующее значение. Таким образом, нахождение оптимального значения целевой функции показывает наиболее верное распределение тех или иных ресурсов при заданных ограничениях. Система ограничений 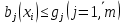 , , 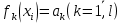 и граничные условия и граничные условия 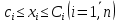 отражают непосредственно ситуацию ограниченности ресурсов в данной конкретной задаче. Ограничения могут быть представлены в виде равенств отражают непосредственно ситуацию ограниченности ресурсов в данной конкретной задаче. Ограничения могут быть представлены в виде равенств 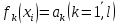 и неравенств и неравенств 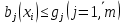 . .Суть подобной постановки задачи заключается в необходимости найти такие значения 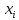 , при которых целевая функция , при которых целевая функция 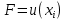 принимала бы оптимальное значение и при которых соблюдались бы все ограничения принимала бы оптимальное значение и при которых соблюдались бы все ограничения 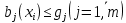 , , 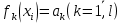 и граничные условия и граничные условия 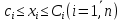 . .С 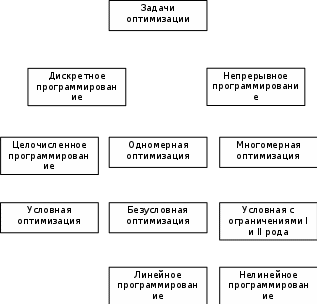 огласно пособию Е.А. Кочегуровой «Теория и методы оптимизации» [3] существует следующая классификация моделей математического программирования (рис. 1.2). огласно пособию Е.А. Кочегуровой «Теория и методы оптимизации» [3] существует следующая классификация моделей математического программирования (рис. 1.2).Рис. 1.2. Классификация моделей математического программирования В данной работе мы рассматриваем лишь задачи условной многомерной оптимизации и более подробно останавливаемся на этой ветви классификации. В зависимости от вида целевой функции различаются два типа задач оптимизации. Примеры, в которых целевая функция имеет линейный вид, называют задачами линейного программирования. Если же целевая функция представлена в виде нелинейной, то и тип проблемы носит название задачи нелинейного программирования. Пример модели задачи линейного программирования: 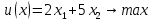 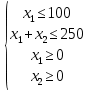 Так как и целевая функция, и все ограничения являются линейными функциями, т.е. функциями, содержащими переменные в степени не выше первой, то и вся система является моделью линейного программирования. Задачи линейного программирования в основном ориентированы на составление рабочих графиков, оптимизацию использования ресурсов сырья на производстве, а также при подсчетах оптимальной доли некоторого вещества (например, пищевых смесей в рационе). Примером модели нелинейного программирования может послужить следующая: 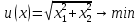 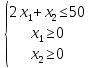 В данном случае функция u(x) включает в себя переменные, степени которых могут превышать первую, однако ограничения остаются линейными. Подобные модели становятся все более востребованными в экономике, практически все экономические задачи выражаются с их помощью, так как тесно связаны с основной экономической задачей. Рассматривается задача о распределении ограниченных ресурсов таким образом, чтобы либо максимизировать эффективность, либо, максимизировать потребление. Нелинейное программирование используется для решения задач составления планов и оптимизации производства, принятия управленческих решений по формированию портфелей ценных бумаг. К случаям применения задач нелинейного программирования подойдут и все, описанные выше для линейного программирования, так как он является частным случаем нелинейной модели. Данная работа посвящена решению задач одного из типов нелинейного программирования, поэтому рассмотрим классификацию данных типов, приведенную в пособии Е.А. Кочегуровой «Теория и методы оптимизации» [3] (рис. 1.3). 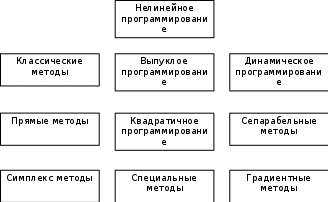 Рис. 1.3. Классификация задач нелинейного программирования Квадратичное программирование как частный случай задачи выпуклого программирования Как видно из рис. 1.3, задача квадратичного программирования является частным случаем задачи выпуклого программирования. Опираясь на знания из курса математического анализа и пособие по Теории системного анализа и принятия решений, мы вводим следующие термины. Функция u(x) называется выпуклой на выпуклом множестве Ω, если для любых двух точек x1 и x2 из множества Ω выполнено следующее неравенство:
где 0 ≤ 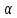 ≤ 1. ≤ 1.Функция u(x) называется вогнутой на выпуклом множестве Ω, если для любых двух точек x1 и x2 из множества Ω выполнено следующее неравенство:
где 0 ≤ 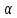 ≤ 1. ≤ 1.Функция будет называться строго выпуклой (строго вогнутой), если неравенства строгие. Вспомним также геометрическое изображение выпуклой (рис. 1.4) и вогнутой (рис. 1.5) функций.   Рисунок 1.4. Выпуклая функция Рисунок 1.5. Вогнутая функция Задачей выпуклого программирования называется частный случай общей задачи максимизации нелинейного программирования, когда целевая функция 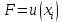 и ограничения и ограничения 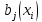 , , 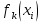 являются вогнутыми на выпуклом множестве Ω. являются вогнутыми на выпуклом множестве Ω. Задача максимизации эквивалентна задаче минимизации, где целевая функция взята со знаком «минус», а значит, будучи вогнутой, становится выпуклой, а в ограничениях также меняется как знак функции, так и знак неравенства. Таким образом, задачей выпуклого программирования называется и задача минимизации нелинейного программирования, где функция 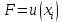 и ограничения и ограничения 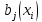 , , 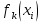 являются выпуклыми на выпуклом множестве Ω. являются выпуклыми на выпуклом множестве Ω.Одним из самых простых типов задач нелинейного математического программирования является квадратичное программирование, так как методика его решения по большей части сводится к алгоритму решения задач линейного программирования. Согласно учебному пособию В. А. Даугавета «Численные методы квадратичного программирования» [1] задачей квадратичного программирования называется задача минимизации квадратичной функции на выпуклом множестве Ω:
Квадратичная функция может быть представлена в виде:
где D – матрица порядка n, c – вектор из 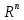 , , 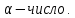 Заметим, что если матрица D не симметрична, то ее можно заменить на симметричную
так как 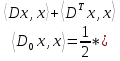 ) = ) = 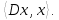 При решении задачи поиска минимума, 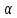 можно отбросить, она на решение не влияет. можно отбросить, она на решение не влияет.Таким образом, нас интересуют способы решения задачи следующего вида:
где матрица D[N,N] симметрична, а
Более того, будем предполагать, что матрица D неотрицательно определена, так что функция F(x) выпукла на 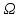 . Таким образом, мы будем рассматривать задачу выпуклого квадратичного программирования (ВКП). Частным случаем такой задачи, когда D = Ο, является задача линейного программирования (ЛП). . Таким образом, мы будем рассматривать задачу выпуклого квадратичного программирования (ВКП). Частным случаем такой задачи, когда D = Ο, является задача линейного программирования (ЛП).Общий вид задачи квадратичного программирования:
где 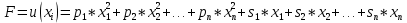 - квадратичная функция, и существует - квадратичная функция, и существует 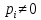 , а ограничения , а ограничения 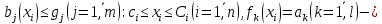 линейны. линейны.Для того чтобы проверить, является ли нелинейная задача выпуклой и существуют ли у нее решения, используют теорему и условия Куна-Таккера. Теорема звучит следующим образом: Если x* - решение некоторой задачи НЛП, то справедливы следующие условия: x* - допустимая точка, то есть существуют такие множители j ≥0, что 1. 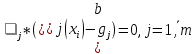 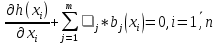 если сама модель имеет вид (1.10). Вывод и доказательство данного утверждения приводится в параграфе 2, пункте 2.4 учебника У. И. Зангвилла «Нелинейное программирование» [2]. Далее мы будем рассматривать различные методы решения задач квадратичного программирования, однако, прежде стоит отметить, что решение любой задачи оптимизации сводится к нахождению максимума или минимума целевой функции, то есть экстремума. Функция u(x), определенная на выпуклом множестве Ω, достигает глобального минимума в точке x*ϵ Ω тогда и только тогда, когда для любого xϵ Ω
Если же для любого xϵ Ω выполняется условие
то точка x*ϵ Ω называется точкой глобального максимума функции h(x) на выпуклом множестве Ω, а u(x*) – глобальным максимумом соответственно. В случае, когда можно указать лишь окрестность ε точки x, в которой выполняется то или иное неравенство, точка x*ϵ Ω будет точкой локального минимума или максимума, а функция u(x) достигает локального экстремума в окрестности точки x*. Функция u(x) называется унимодальной на некотором отрезке [a,b], где x ϵ [a,b], если на этом отрезке локальный экстремум функции совпадает с глобальным. Понятие унимодальности является важным в теории оптимизации, потому что многие методы решения задач линейного и нелинейного программирования требуют выполнение этого условия. Таким образом, изучение задач оптимизации нацелено на получения наиболее точного значения экстремума за наикратчайший промежуток времени. Так как типы целевых функций и ограничений различны, то различаются и методы решения задач линейного и нелинейного программирования. Далее мы познакомимся с методами решения задач квадратичного программирования. Методы решения задач квадратичного программирования Опираясь на классификацию методов нелинейного программирования, можно составить следующую таблицу: Таблица 1.1. Классификация методов решения задач НЛП
Если рассматривать классификацию по наличию ограничений, то задачи без ограничений называются также безусловной оптимизацией и примером метода решения подобной задачи может служить метод покоординатного спуска, а задачи с ограничениями – условной оптимизацией (например, симплекс-метод). В зависимости от возможности найти данным методом точное или приближенное значение экстремума целевой функции различают точные (метод перебора граней) и итерационные методы (метод деления пополам). Зная количество координат вектора x, мы можем выделить задачи, в которых используется вектор размерности один, то есть одномерные (метод исключения интервалов) и задачи, где размерность вектора x превышает единицу – многомерные (графический метод). В случае, если в алгоритме решения задачи используется только сама целевая функция и ее значения, применяют методы прямого поиска (метод Хука-Дживса), если же в процессе решения появляются первые или вторые производные, значит, используемый метод носит название градиентного метода первого или второго порядка соответственно (метод множителей Лагранжа). Следует заметить, что существует огромное количество методов, и ни один из них не является универсальным, при решении каждой конкретной задачи приходится подбирать и приспосабливать наиболее подходящий метод. Далее в данной главе будут затронуты алгоритмы решения задач квадратичного программирования некоторыми методами, а в следующей части работы рассмотрим конкретные примеры. В ходе настоящего исследования мы рассмотрим следующие методы решения задач квадратичного программирования: Метод множителей Лагранжа Симплекс-метод Графический метод Далее будут представлены алгоритмы вышеупомянутых методов, а также основные теоремы, использующиеся в ходе этих алгоритмов. Основная задача метода множителей Лагранжа состоит в том, чтобы преобразовать исходную задачу оптимизации с ограничениями к безусловному виду. Пусть имеется следующая задача оптимизации:
В первую очередь, целевая функция 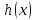 проверяется на выпуклость или вогнутость, в зависимости от поиска минимума или максимума целевой функции, соответственно. проверяется на выпуклость или вогнутость, в зависимости от поиска минимума или максимума целевой функции, соответственно.Прямое отношение к задаче НЛП имеет функция Лагранжа:
где =(1, 2, … l), 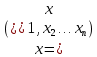 Справедливость данного равенства, а также эквивалентности систем (1.12) и (1.13) доказана в параграфе 2.6. учебника У. И. Зангвилла «Нелинейное программирование» [2] Следовательно, оптимизационная задача приведена в безусловный вид, и требуется найти неизвестные =(1, 2, … l), 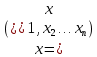 . Считаются частные производные функции L(x,) по этим переменным. Для того, чтобы существовал локальный экстремум функции u(x) в системе (1.12), необходимо найти решение следующей системы: . Считаются частные производные функции L(x,) по этим переменным. Для того, чтобы существовал локальный экстремум функции u(x) в системе (1.12), необходимо найти решение следующей системы:
Доказательство этого утверждения приведено в учебнике «Теория экстремальных задач» А. Д. Иоффе, В. М. Тихомирова [4] во второй главе, параграфе 2.3, Теорема 1. Таким образом, решение системы (1.14) 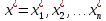 является решением исходной задачи оптимизации системы (1.14), в случае, если матрица Гессе является решением исходной задачи оптимизации системы (1.14), в случае, если матрица Гессе
положительно определена. Симплекс-метод считается одним из стандартных методов решения задач линейного программирования, однако некоторые из таких методов, и, в частности, симплекс-метод, могут быть применены для решения задач нелинейного программирования. По большому счету симплекс-метод является методом перебора. Среди кандидатов на экстремум рассматриваются вершины выпуклого многогранника, составленного по ограничениям. Симплекс-метод применим только к задачам с ограничениями вида неравенств, поэтому первым этапом этого метода становится приведение системы ограничений:
к каноническому виду:
Затем в линейном случае в соответствии с системой (1.17) составляется таблица коэффициентов. Таблица 1.2. Симплекс-метод
где c1..cn – коэффициенты при переменных xi в целевой функции. |

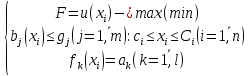
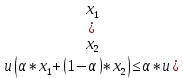 ,
,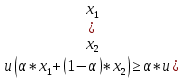 ,
,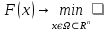
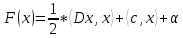 ,
, 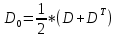 ,
, 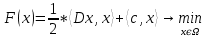 ,
, 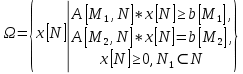 .
. 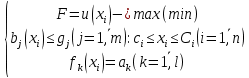
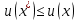 .
. 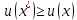 ,
,