Диплом 1 Ракова. Квадратичное программирование
 Скачать 106.64 Kb. Скачать 106.64 Kb.
|
|
Применение методов для решения примера задачи квадратичного программирования В этом разделе рассматривается задача квадратичного программирования на примере ООО «Воронежский литейный завод». На основе исходных данных составляется математическая модель, выбирается алгоритм решения задачи и анализируется результат. Задача. На ООО «Воронежский литейный завод» производится два комплекта изделий – деталей для сельскохозяйственных машин. Первый комплект состоит из ОВИ-02101 и ОВИ-03101, второй комплект – ЗС-1038 и ЗП-04103. Первая смена работников специализируется на производстве ОВИ-02101 и ЗС-1038. Суточная норма работы Смены 1 выражается в числе выплавок печи и составляет 1600 кг/день. Смена 2 делает ОВИ-03101 и ЗП-04103. Суточная норма работы второй смены – 1400 кг/день. Вес каждой детали с учетом веса литниковой системы (считаем сырье в ней невозвратным) представлен в таблице 2.6. Цены деталей зависят от спроса и потому могут быть выражены формулами. Необходимые для составления формул статистические данные о среднем спросе на товар и его цены за два периода представлены в таблице 2.7. Себестоимость каждого типа деталей в комплекте из расчета на килограммы представлена в таблице 2.8. Таблица 2.6. Вес деталей
Таблица 2.7. Спрос
Таблица 2.8. Себестоимость
Детали представляют ценность и закупаются лишь в комплекте. Причем в комплект 1 входят две детали типа ОВИ-02101 и одна деталь ОВИ-03101, а в комплект 2 – две детали ЗС-1038 и одна ЗП-04103. Требуется составить план дневного производства деталей, удовлетворяющий перечисленным выше требованиям и оптимизирующий прибыль предприятия. В соответствии с поэтапным алгоритмом, представленным на рис. 1.1, следует составить модель решения данной задачи. Обозначим объемы производства комплектов 1 и 2 через переменные x1 и x2 соответственно. Чтобы составить целевую функцию 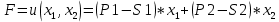 , ,где P1, P2 – цены на комплекты 1 и 2 соответственно, S1, S2 – себестоимости комплектов 1 и 2 соответственно, требуется найти формулы для цены на детали. Общий вид формулы спроса: 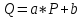 , чтобы выразить Р, составим систему уравнений с данными из Таблицы 2.2 и найдем коэффициенты a и b. , чтобы выразить Р, составим систему уравнений с данными из Таблицы 2.2 и найдем коэффициенты a и b.Система уравнений для комплекта 1: 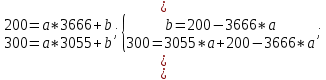 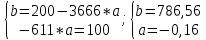 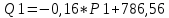 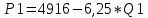 Система уравнений для комплекта 2: 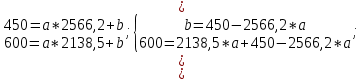 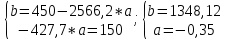 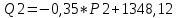 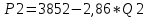 Целевая функция максимизации прибыли в соответствии с условием и полученными формулами будет выглядеть следующим образом: 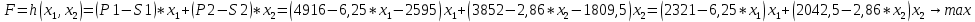 На целевую функцию наложены следующие ограничения: 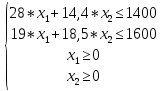 Итак, первый этап закончен – задача поставлена. Далее предстоит выбрать метод решения задачи. Из описанных выше методов Метод множителей Лагранжа не может быть применен, так как в условии задачи есть ограничения, выраженные неравенствами, а симплекс-метод второго типа и графический метод неудобно использовать, потому что в задаче используются дробные числа. Воспользуемся симплекс-методом с применением функции Лагранжа для решения поставленной задачи оптимизации квадратичного вида. Определим вершины многогранника ограничений с помощью решения совокупности систем неравенств: 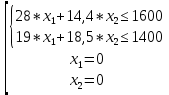 Вершины многогранника ограничений представлены в таблице: Таблица 2.9. Вершины многогранника ограничений
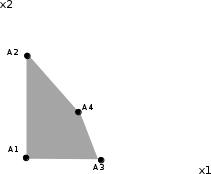 Рисунок 2.3. Многогранник ограничений Заштрихованная область – многогранник ограничений. На следующем этапе мы производим поиск решения на гранях многогранника ограничений. Для этого составляются и решаются системы уравнений (1.19): 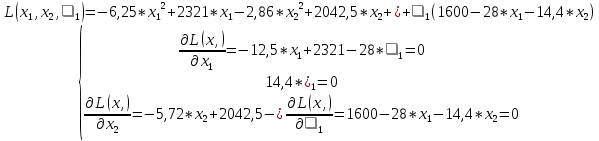 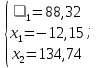 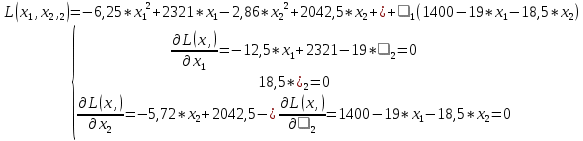 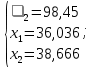 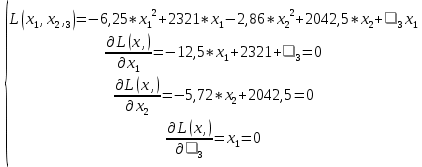 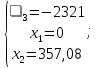 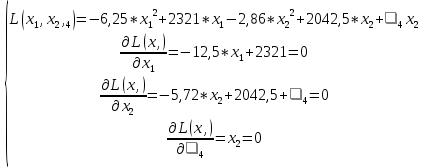 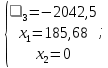 Составим таблицу координат точек, подозрительных на экстремум и значений целевой функции в этих точках: Таблица 2.10. Точки, подозрительные на экстремум
Максимальное значение целевой функции дает точка (0; 357,08), однако она не входит в многогранник ограничений. Единственная точка, входящая в многогранник ограничений – (36,036;38,666). Значение целевой функции в ней равно 149008,51. Таким образом, для того, чтобы оптимизировать производство данных комплектов товаров, необходимо производить 37 комплектов первого типа и 39 комплектов второго типа ежедневно. В этом случае прибыль составит 149008,51. Если на данный момент объемы производства превышают получившийся результат и товар в избытке, то заводу следует искать новые каналы сбыта товара, если же объемы производства меньше, то есть имеет место дефицит, то требуется организационная и технологическая модернизация производства с целью устранения перекосов в технологической цепи и определения зон дополнительного инвестирования. Следует также учесть, что в задаче намерено не были учтены многие факторы, например, процент брака, количество деталей, отливаемых в одной опоке (форме), возможность переплавки чугуна из литниковой системы и другие. Решение задач с учетом перечисленных и иных факторов может являться направлением для дальнейшего исследования и развития настоящей работы. ЗАКЛЮЧЕНИЕ В ходе исследования были сделаны следующие выводы и получены следующие результаты. Для грамотной реализации поставленной задачи оптимизации квадратичного типа была изучена природа задач оптимизации, основные цели их формирования и прикладного использования в экономических науках. Для освещения возможности решения подобных экономических задач математическими методами были проанализированы модели задач оптимизации линейного и нелинейного типов, их общий вид, основные типы функций, входящих обыкновенно в систему оптимизационной модели. Акцентировано внимание на различных этапах и алгоритмах основных методов решения оптимизационных задач, с целью использовать полученные знания при решении примеров. Были рассмотрены элементарные методы (метод множителей Лагранжа, симплекс-метод, графический метод), которые на практике чаще используются в совокупности или как составляющие элементы более сложных способов. Практическая часть работы была разделена на две части. Первая из них включила в себя примеры наглядного применения вышеупомянутых методов. Данные задачи позволили понять структуру схемы работы каждого метода и его действия в случае решения задачи квадратичного типа, увидеть преимущества и недостатки использования каждого из методов в отдельности, проанализировать скорость решения и оценить математический аспект. Второй раздел практической части данной бакалаврской работы содержит в себе непосредственное формирование и решение прикладной задачи оптимизации квадратичного типа на примере ООО «Воронежский литейный завод». Для решения задачи были применены полученные знания из теоретического обзора и вышерассмотренного первого раздела практической части. В ходе исследования была проанализирована промышленная деятельность ООО «Воронежский литейный завод» и выявлены возможности оптимизации производства посредством составления и решения соответствующей задачи оптимизации. Математическая модель задачи была составлена исходя из предоставленных заводом данных. Метод решения поставленной задачи был выбран на основании решения упомянутых примеров, анализа процесса нахождения результата и анализа самой структуры метода. В ходе решения был соблюден алгоритм симплекс-метода с использованием функции Лагранжа. Полученные результаты могут быть применены заводом для оптимизации производственного процесса, анализ решения может служить предпосылкой для рассмотрения более детальной задачи, учитывающей большее число факторов, что является направлением для дальнейшего исследования. СПИСОК ЛИТЕРАТУРЫ 1. Даугавет В. А. Численные методы квадратичного программирования : учебное пособие / В. А. Даугавет ; С.-Петерб. гос. ун-т .— СПб. : Изд-во С.-Петерб. ун-та, 2004 .— 127 2. Зангвилл У. И. Нелинейное программирование : Единый подход / У.И. Зангвилл ; Пер. с англ. Д.А. Бабаева; Под ред. Е.Г. Гольштейна .— М. : Советское радио, 1973 .— 310 3. Кочегурова Е. А. Теория и методы оптимизации / Е. А. Кочегурова ; Томский политехнический университет. – Томск: Изд-во Томского политехнического университета, 2012. – 157 с. 4. Иоффе А. Д. Теория экстремальных задач / А.Д. Иоффе, В.М. Тихомиров .— М. : Наука, 1974 .— 479 с. 5. Ларичев О. И. Теория и методы принятия решений, а также Хроника событий в Волшебных Странах : [учебник для студ. вузов] / О.И. Ларичев .— Изд. 3-е, перераб. и доп. — М. : Физматкнига : Логос, 2006 .— 390 6. Емельянов С.В. Многокритериальные методы принятия решений / С.В. Емельянов, О.И. Ларичев .— М. : Знание, 1985 .— 30 7. Фролов В. Н. Прикладные задачи моделирования и оптимизации : Межвуз.сб.науч.тр. / Воронеж.гос.техн.ун-т; Редкол.: В.Н.Фролов(отв.ред.) и др. — Воронеж, 1998 .— 176c. 8. Еремин И. И. Теория линейной оптимизации / И.И. Еремин ; РАН. УРО. Ин-т математики и механики; Отв. ред. Л.Д. Попов .— Екатеринбург, 1999 .— 312 с. 9. Тынкевич М.А. Экономико-математические методы (исследование операций) / М.А. Тынкевич . : Кузбасский государственный технический университет – Изд. 2 испр. и доп. – Кемерово, 2000. – 177 с. 10. Еремин И. И. Вопросы оптимизации и распознавание образов : Метод.пособие / О-во "Знание" УНЦ АН СССР.Нар.ун-т мат. и вычисл.техники ; И. И. Еремин, В. Д. Мазуров .— Свердловск : Средне-Урал.кн.изд-во, 1979 .— 60,[3] c. 11. Годунов Б.А. О некоторых задачах математического программирования : Дис. ...канд.физико-мат.наук / Науч.рук.Я.Б.Рутицкий;Воронеж.инж.-строит.ин-т .— Воронеж, 1972 .— 107с. 12. Карманов В. Г. Математическое программирование / В. Г. Карманов .— 5-е изд., испр. — М. : Физматлит, 2000 .— 263 с. 13. Абрамов Л. М. Математическое программирование : Теория выпуклого программирования / Л.М. Абрамов, В.Ф. Капустин ; С.-Петерб. гос. ун-т .— СПб. : Изд-во С.-Петерб. ун-та, 2001 .— 259, [2] с. 14. Галеев Э. М. Оптимизация : Теория. Примеры. Задачи / Э. М. Галеев, В. М. Тихомиров .— М. : Эдиториал УРСС, 2000 .— 317 с. 15. Квадратичное программирование [Электронный ресурс] – Режим доступа: http://iasa.org.ua/lections/iso/5/5.5.htm 16. Методы оптимизации [Электронный ресурс] – Режим доступа: http://pgtk.edu.ru/legacy/lection/mat_met/math_met/function.htm 17. Метод Лагранжа [Электронный ресурс] – Режим доступа: http://www.intuit.ru/studies/courses/1020/188/lecture/4925?page=2 18. Симплекс-метод [Электронный ресурс] – Режим доступа: http://pfkpi.nnstr.com/EMM/Task05.htm 19. Теория экстремальных задач [Электронный ресурс] – Режим доступа: http://chem21.info/page/043023183035140197075006088178116142202169044110/ 20. Виды задач оптимизации [Электронный ресурс] – Режим доступа: http://admeral1.narod.ru/files/kipiasu/sau/2_3_7_2.pdf 21.Применение нелинейного программирования в экономике, управлении и хозяйственных областях [Электронный ресурс] – Режим доступа: http://studopedia.su/7_48943_primenenie-nelineynogo-programmirovaniya-v-ekonomike-upravlenii-i-hozyaystvennih-oblastyah.html 22. Экономико-математическое моделирование [Электронный ресурс] – Режим доступа: http://www.e-ng.ru/ekonomiko-matematicheskoe_modelirovanie/matematicheskie_zadachi_issledovaniya.html 23. Задача линейного программирования [Электронный ресурс] – Режим доступа: http://window.edu.ru/resource/881/40881/files/dvgu002.pdf 24. Метод решения задач квадратичного программирования [Электронный ресурс] – Режим доступа: http://studopedia.ru/8_121708_metod-resheniya-zadach-kvadratichnogo-programmirovaniya.html 25. Квадратичный симплекс-метод [Электронный ресурс] – Режим доступа: http://allrefs.net/c20/47f4b/p38/ ПРИЛОЖЕНИЕ Основные определения График функции – множество всех точек координатной прямой, абсциссы которых равны значениям аргумента, а ординаты - соответствующим значениям функции. Литниковая система — система каналов и полостей в форме, через которые жидкий расплавленный материал – расплав (металл или пластик) подается в полость литьевой формы или пресс-формы для литья под давлением. Математическая модель — приближенное описание объекта моделирования, выраженное с помощью математической символики. Математическое программирование — это область математики, разрабатывающая теорию, численные методы решения многомерных задач с ограничениями. В отличие от классической математики, математическое программирование занимается математическими методами решения задач нахождения наилучших вариантов из всех возможных. Линия уровня функции – множество точек из ее области определения, в которых функция принимает одно и то же фиксированное значение. Нелинейное программирование — случай математического программирования, в котором целевой функцией или ограничением является нелинейная функция. Область определения или область задания функции — множество, на котором задаётся функция. В каждой точке этого множества значение функции должно быть определено. Оптимизация — в наиболее общем случае: выбор наилучшего (оптимального) варианта из множества возможных. В экономике — определение значений экономических показателей, при которых достигается оптимум, то есть оптимальное, наилучшее состояние системы. Чаще всего оптимуму соответствует достижение наивысшего результата при данных затратах ресурсов или достижение заданного результата при минимальных ресурсных затратах. Решение системы уравнений – вектор значений переменных, обращающий каждое уравнение системы в верное числовое равенство, другими словами, являющийся решением каждого уравнения системы. Система уравнений – это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных. Стационарные точки – точки, в которых производная функции равна нулю. Точки, подозрительные на экстремум – стационарные точки и точки, в которых не существует двусторонней конечной производной. Точка экстремума – точка, в которой достигается экстремум. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. Функция – закон, в соответствии с которым каждому элементу одного множества ставится единственный элемент другого множества. Другими словами, взаимосвязь между величинами. Целевая функция — вещественная или целочисленная функция нескольких переменных, подлежащая оптимизации (минимизации или максимизации) в целях решения некоторой оптимизационной задачи. Частная производная — одно из обобщений понятия производной на случай функции нескольких переменных. Частная производная — это предел отношения приращения функции по выбранной переменной к приращению этой переменной, при стремлении этого приращения к нулю. Экстремум — максимальное или минимальное значение функции на заданном множестве. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
