Диплом 1 Ракова. Квадратичное программирование
 Скачать 106.64 Kb. Скачать 106.64 Kb.
|
Часть данной таблицы 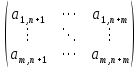 является единичной матрицей по построению. Элементы ri определяются следующим образом: среди ci выбирается максимальный по модулю отрицательный элемент. Он определяет над собой разрешающий столбец s. является единичной матрицей по построению. Элементы ri определяются следующим образом: среди ci выбирается максимальный по модулю отрицательный элемент. Он определяет над собой разрешающий столбец s. 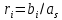 , где , где 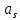 – соответствующий элемент разрешающего столбца, причем – соответствующий элемент разрешающего столбца, причем 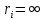 , если , если 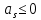 или или 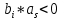 . Среди . Среди 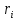 выбирается наименьший, и он определяет разрешающую строку q. На пересечении разрешающего столбца и разрешающей строки оказывается разрешающий элемент выбирается наименьший, и он определяет разрешающую строку q. На пересечении разрешающего столбца и разрешающей строки оказывается разрешающий элемент 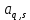 . . В линейном случае этот этап называется этапом выбора опорного плана или выбором главного элемента. Весь метод похож на метод Гаусса с выбором главного элемента. После выбора главного элемента 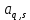 заполняется новая таблица, элементы которой соответствуют следующей формуле: заполняется новая таблица, элементы которой соответствуют следующей формуле: 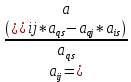 . . Поиск оптимального решения заканчивается, когда для любого 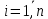 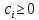 . В этом случае решением системы становится элемент F. . В этом случае решением системы становится элемент F.В квадратичном и любом другом нелинейном случае существует несколько возможных применений симплекс-метода. В одном из них в первую очередь составляется таблица вершин многогранника ограничений, в которой рассматриваются вершины, где хотя бы одна координата равна 0 и непосредственное решение 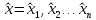 системы системы 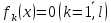 . В последний столбец таблицы записываются значения целевой функции при данных значениях координат вершин. . В последний столбец таблицы записываются значения целевой функции при данных значениях координат вершин. Таблица 1.3. Вершины многогранника ограничений
На втором этапе ищется решение оптимизационной задачи на гранях многогранника ограничений. Для этого для каждого ограничения составляется функция Лагранжа, и от нее находятся частные производные по каждой переменной. Получаем систему:
где 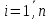 . Таких систем будет l, так как . Таких систем будет l, так как 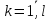 . .Для каждой системы мы находим решения xi, эти точки будут подозрительными на точки экстремума, и значение целевой функции 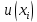 . Наконец, мы выбираем наименьший или наибольший из получившихся результатов. Если эта вершина находится на грани многогранника ограничений, то она является точкой экстремума, а значение целевой функции в этой точке – экстремумом и решением заданной задачи оптимизации. . Наконец, мы выбираем наименьший или наибольший из получившихся результатов. Если эта вершина находится на грани многогранника ограничений, то она является точкой экстремума, а значение целевой функции в этой точке – экстремумом и решением заданной задачи оптимизации.Существует и другой вариант применения симплекс-метода при решении квадратичных оптимизационных задач. Сначала проверяется, является ли данная нелинейная задача задачей квадратичного типа. Это проверяется по Теореме Куна-Таккера, формулировка и доказательство которой приведены в учебнике «Теория экстремальных задач» А. Д. Иоффе, В. М. Тихомирова [4] в первой главе, раздел 1.3. Далее начинается сам процесс нахождения решения задачи симплекс-методом. В первую очередь требуется составить функцию Лагранжа по формуле (1.13). Записываются необходимые и достаточные условия существования седловой точки функции Лагранжа – условия Куна-Таккера:
Данную систему можно записать в каноническом виде
где vi и wk – вспомогательные переменные. Тогда это становится задачей линейного программирования. В качестве целевой функции вводим новую функцию
где M – вектор произвольных коэффициентов, значительно превышающих значения коэффициентов исходной целевой функции u(xi). Теперь мы имеем задачу линейного типа и можем решать ее стандартным симплекс-методом, за одним исключением, что в базис не могут входить одновременно основные и вспомогательные переменные с одинаковыми индексами. Для соблюдения этого критерия требуют выполнение следующих условий:
Кроме того, оптимальное решение не может содержать искусственных переменных ti, поэтому оптимальное решение будет достигнуто, как только в таблице все значения z будут равны нулю. Графический метод является одним из самых наглядных и зачастую быстрых методов решения задач оптимизации. Однако, он не может быть применим, если задача выражена через математическую модель со сложной целевой функцией или функцией размерности больше, чем три. Основная суть метода – отображение графиков всех функций (как целевой, так и ограничений) на одной координатной плоскости, и выбор оптимального решения в соответствии с графиками, их пересечениями и допустимыми значениями. На декартовой плоскости изображаются множество линий уровня квадратичной целевой функции и линии ограничений, где знак неравенства отображается как заштрихованная часть плоскости или пространства. Область пересечения этих частей называется множеством допустимых значений функции, и решение задачи оптимизации должно принадлежать этой области. Обязательным ограничением в любой задаче оптимизации является условие неотрицательности координат, поэтому данные области всегда ограничены положительными частями координатных осей. Точками, подозрительными на экстремум, становятся точки касания линий уровня целевой функции с графиками ограничений. Координаты этих точек подставляются в уравнение целевой функции и полученные значения сравниваются. Графический метод часто применяется не только как самостоятельный способ решения оптимизационных задач, но и как дополнительный этап какого-либо другого метода. Так, например, элементы графического метода часто входят в рассмотренный выше симплекс-метод. Подводя итоги, отметим, что в данной главе были проанализированы основные методы решения квадратичных оптимизационных задач. Далее будут приведены конкретные примеры решения нелинейных задач оптимизации квадратичного типа данными способами по отдельности и в совокупности. ПРАКТИЧЕСКАЯ ЧАСТЬ Решение задач квадратичного программирования методом множителей Лагранжа, симплекс-методом и графическим методом В этой главе мы рассматриваем несколько примеров решения задач вышеперечисленными методами. Первую квадратичную задачу предлагается решить методом множителей Лагранжа. Дано условие: 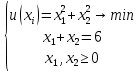 Составим функцию Лагранжа по формуле (1.13): 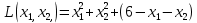 Как и описано в алгоритме метода в предыдущей главе, теперь следует посчитать частные производные в соответствии с системой (1.14): 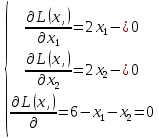 Найдем значения неизвестных 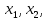 . . 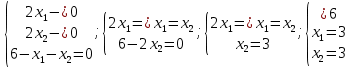 Проверим определенность матрицы Гессе (1.15): 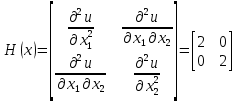 =4 =4Матрица определена положительно, и все элементы главной диагонали также положительны, следовательно, точка x*=(3,3) – стационарная точка, а значение целевой функции в этой точке u(x*) = 18 – минимум, то есть решение задачи оптимизации. В качестве следующего примера решается задача оптимизации симплекс-методом с применением функции Лагранжа. В данном методе уже возможно решение задач с ограничениями в виде неравенств. Условие задачи следующее: 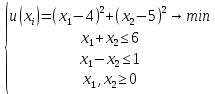 Определим вершины многогранника ограничений (Таблица 1.3). Таблица 2.1. Вершины многогранника ограничений
Координаты точек находятся из решения совокупности: 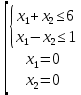 Вторым этапом осуществляется поиск решения на гранях многогранника ограничений. Для этого составляются и решаются системы уравнений (1.19): 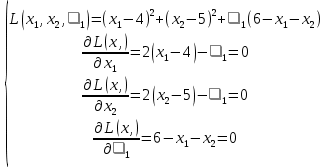 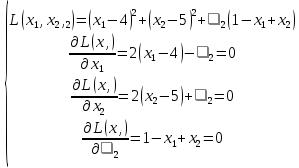 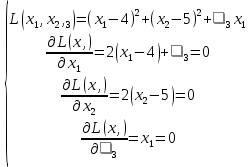 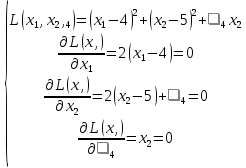 Найдем решения систем: 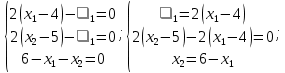 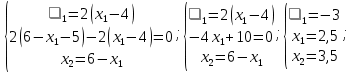 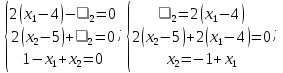 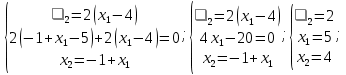 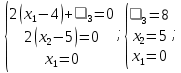 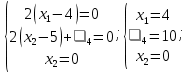 Составим таблицу координат точек, подозрительных на экстремум и значений целевой функции в этих точках: Таблица 2.2. Координаты подозрительных точек
Так как по условию задачи необходимо найти минимум, то точкой экстремума будет точка (5; 4), а минимумом – u(x)=2. Однако, эта точка выходит за грани многогранника ограничений, а, следовательно, не может быть решением. Значит точка экстремума – (2,5; 3,5), а минимум - u(x)=4,5. Эта точка принадлежит многограннику ограничений и лежит на его грани, а значит, удовлетворяет всем условиям, и значение целевой функции в этой точке – ответ задачи. Далее приведено решение задачи оптимизации вторым вариантом симплекс-метода, описанного в предыдущей главе. Дана квадратичная задача: 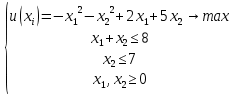 Составим уравнение Лагранжа (1.13): 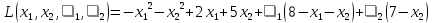 Запишем условия Куна-Таккера (1.19) и (1.20): 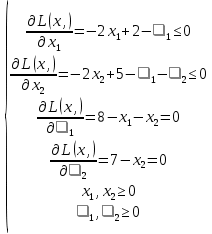 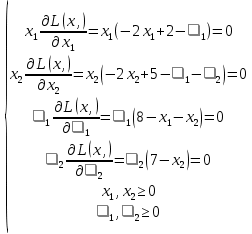 Чтобы перейти к линейной системе и решать ее симплекс-методом, необходимо привести ограничения к каноническому виду: 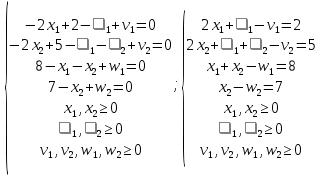 В качестве целевой функции возьмем функцию: 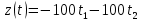 Составим симплекс-таблицу 1 (Таблица 1.2): Таблица 2.3. Симплекс-таблица 1
Продолжение таблицы 2.3.
Симплекс-таблица 2: Таблица 2.4. Симплекс-таблица 2
Симплекс-таблица 3: Таблица 2.5. Симплекс-таблица 3
Если в таблице все значения функции z нулевые, то базис найден. Следовательно, целевая функция достигает своего максимального значения при x1=1, x2=5/2, w1=9/2, w2=9/2. Максимум равен h(x) = 7,25. Далее представлено решение первых двух примеров в графическом виде. Условие первой задачи было следующим: 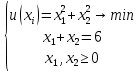 На графической плоскости изображаются линии уровня целевой функции и график ограничения.  Рисунок 2.1. Графическое представление линий уровня и ограничений Так как в задаче ограничения представлены в виде равенства, то решением задачи будет точка касания одной из линий уровня целевой функции графика ограничения. В данном случае по графику видно, что этой точкой будет точка x*=(3,3), и, подставив ее координаты в уравнение целевой функции, мы получим u(x*) = 18, что и будет минимумом. Это значение совпадает с результатом, полученным при решении этой же задачи другим методом. Результат второго примера также несложно проверить, решив его графическим способом. 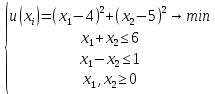 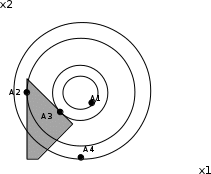 Рисунок 2.2. Графическое решение примера Серая область – многогранник ограничений. На декартовой плоскости обозначены точки касания линий уровня целевой функции с линиями ограничений. Эти точки подозрительные на точки экстремума. Тем не менее, точка может быть точкой экстремума и решением задачи, только если она лежит на грани этого многогранника. Поэтому точки А1 и А4 не могут быть решениями. Между точками А2 и А3 можно выбрать, подставив их координаты в целевую функцию. Решением становится та, при подстановке которой получается меньшее значение. В данном случае, это точка (2,5; 3,5), а значение целевой функции в ней - u(x)=4,5. Итак, в данном подразделе были рассмотрены примеры применения основных методов решения задач оптимизации квадратичного типа с целью изучить принцип действия алгоритмов решения и использовать их в дальнейшем при решении поставленной прикладной задачи. |

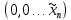
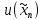
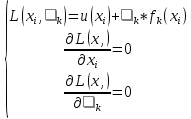 ,
, 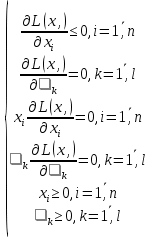
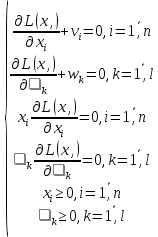 ,
,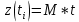 ,
, 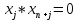 , j
, j